ỹi	ỹi -yi	(ỹi -yi )2	(xi1-x1)2	Sy	1,761Sy	ỹн	ỹв
14,25	-0,15	0,02	0,04	0,07	0,12	14,13	14,37
17,21	0,31	0,10	3,29	0,09	0,16	17,05	17,37
12,77	-0,23	0,05	1,41	0,08	0,14	12,63	12,91
9,81	0,21	0,04	10,16	0,12	0,22	9,59	10,03
9,81	0,01	0,00	10,16	0,12	0,22	9,59	10,03
9,81	0,21	0,04	10,16	0,12	0,22	9,59	10,03
17,21	0,41	0,17	3,29	0,09	0,16	17,05	17,37
14,25	-0,55	0,30	0,04	0,07	0,12	14,13	14,37
9,81	0,01	0,00	10,16	0,12	0,22	9,59	10,03
17,21	0,31	0,10	3,29	0,09	0,16	17,05	17,37
15,73	-0,27	0,07	0,66	0,07	0,13	15,60	15,86
17,21	-0,19	0,04	3,29	0,09	0,16	17,05	17,37
17,21	0,01	0,00	3,29	0,09	0,16	17,05	17,37
17,21	-0,19	0,04	3,29	0,09	0,16	17,05	17,37
15,73	0,03	0,00	0,66	0,07	0,13	15,60	15,86
17,21	0,11	0,01	3,29	0,09	0,16	17,05	17,37
Σ		0,9848	66,44

---

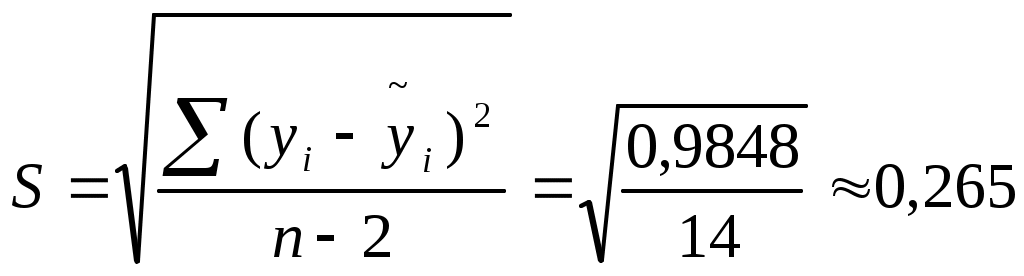, для каждого x_i1 рассчитаем
,

, где . Результаты расчетов для каждого приведены в таблице 4.

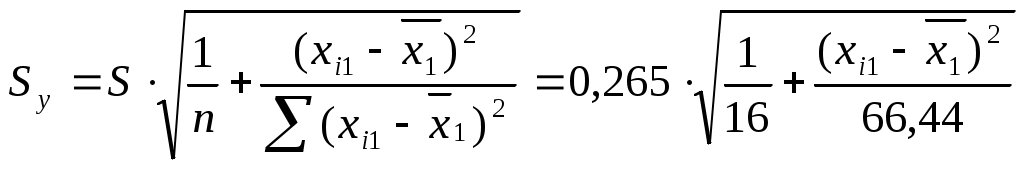Значения 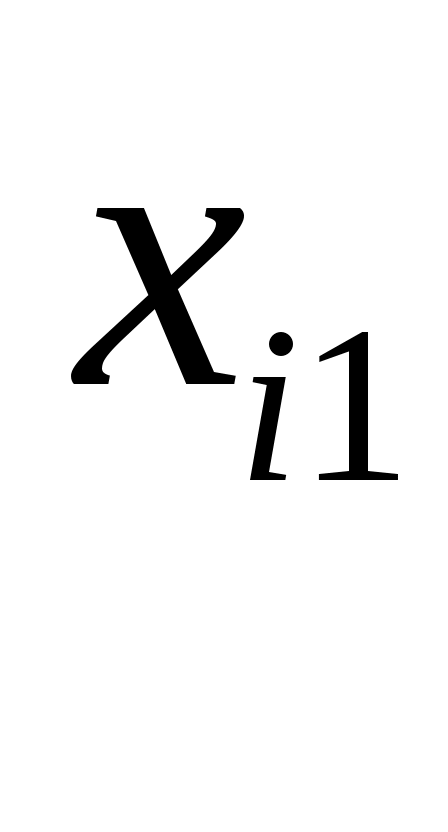определяют доверительный интервал для каждого . Линию регрессии и доверительную полосу изобразим на рисунке 1.
Найдем доверительную полосу для уравнения регрессии , построим вспомогательную таблицу: (таблица 5)

ỹi	ỹi -yi	(ỹi -yi )2	(xi2-x2)2	Sy	1,761Sy	ỹн	ỹв
15,09	0,69	0,48	6,57	0,25	0,45	14,64	15,54
15,31	-1,59	2,53	12,69	0,26	0,45	14,86	15,76
13,99	0,99	0,98	5,94	0,25	0,45	13,54	14,44
9,37	-0,23	0,05	549,32	0,52	0,91	8,46	10,28
10,69	0,89	0,79	304,07	0,42	0,74	9,95	11,43
9,15	-0,45	0,20	597,19	0,54	0,94	8,21	10,09
15,75	-1,05	1,10	30,94	0,27	0,48	15,27	16,23
16,41	1,61	2,59	73,32	0,30	0,53	15,88	16,94
10,69	0,89	0,79	304,07	0,42	0,74	9,95	11,43
15,09	-1,81	3,28	6,57	0,25	0,45	14,64	15,54
16,63	0,63	0,40	91,44	0,31	0,55	16,08	17,18
17,95	0,55	0,30	242,19	0,39	0,69	17,26	18,64
17,07	-0,13	0,02	133,69	0,34	0,59	16,48	17,66
17,07	-0,33	0,11	133,69	0,34	0,59	16,48	17,66
15,31	-0,39	0,15	12,69	0,26	0,45	14,86	15,76
16,85	-0,25	0,06	111,57	0,32	0,57	16,28	17,42
Σ		13,8344	2615,9375

---

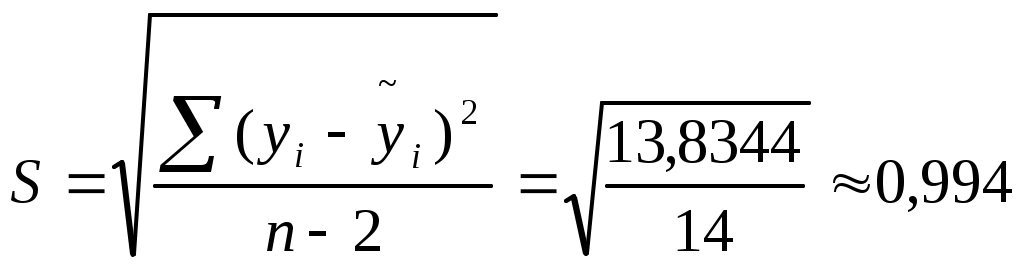, для каждого x_i1 рассчитаем
,

, где . Результаты расчетов для каждого приведены в таблице 5.

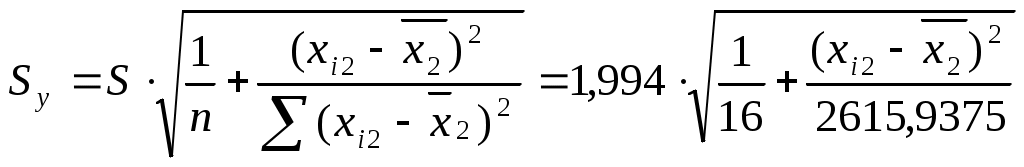Значения определяют доверительный интервал для каждого . Линию регрессии и доверительную полосу изобразим на рисунке 2.

1.6. На продажу поступила очередная партия однотипных автомобилей, их возраст 3 года, мощность 165 л.с. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей в зависимости от возраста и мощности двигателя с доверительной вероятностью 0,9.
В зависимости от возраста:

Точечный прогноз:

Интервальный: , для x₀₁ рассчитаем
,

, где .





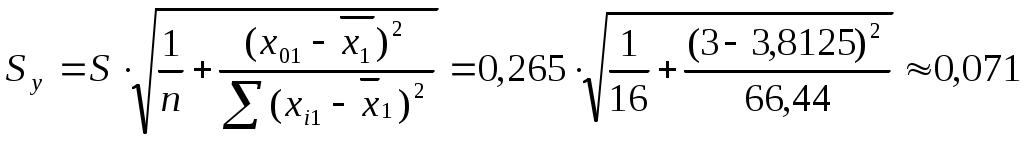т.е. получили доверительный интервал (15,6 ; 15,86).

В зависимости от мощности:

Точечный прогноз:

Интервальный: S = 0,994;

---

, где



, т.е., получили доверительный интервал (16,87 ; 18,15).

---

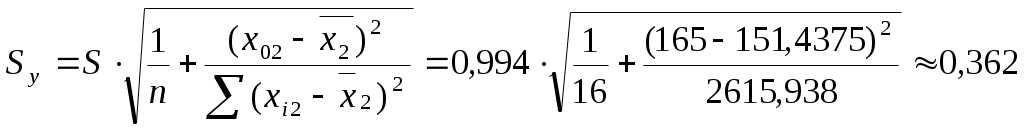
2. Множественная зависимость.
2.1. По методу наименьших квадратов найти оценки коэффициентов множественной линейной регрессионной модели

Составим матрицы 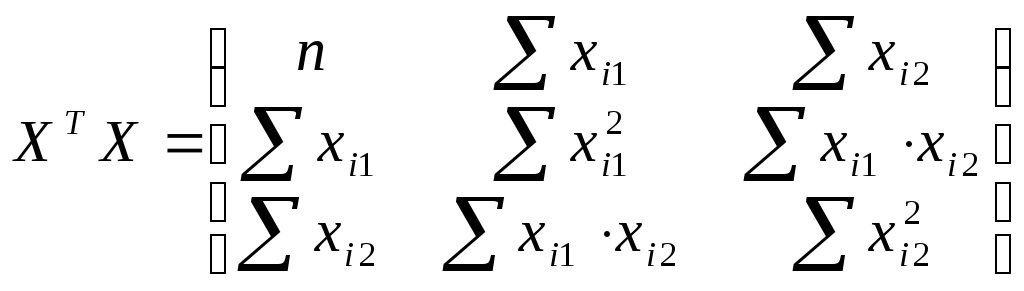и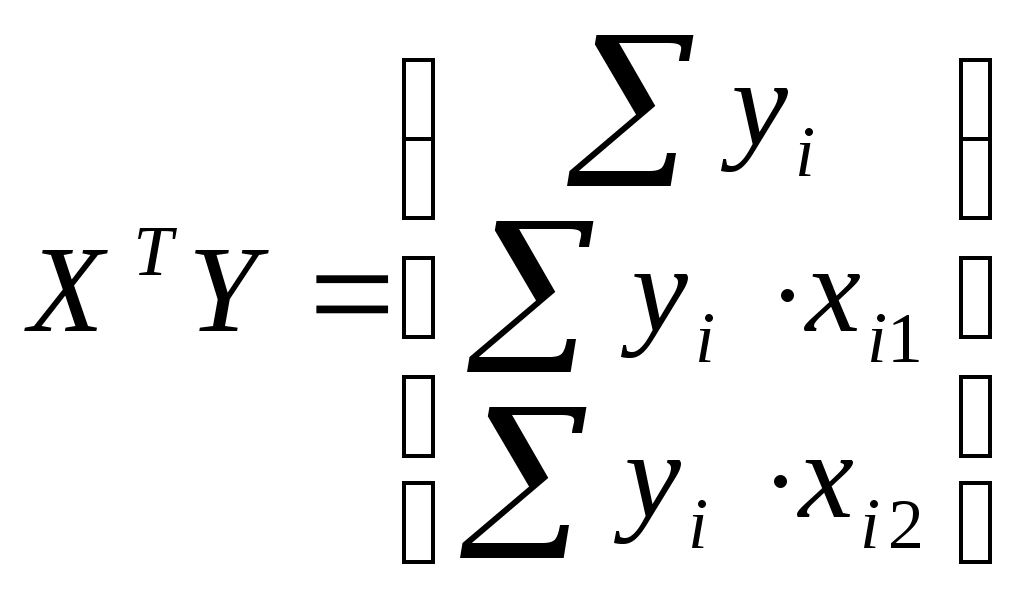

Для этого составим вспомогательную таблицу: (таблица 6)

i	yi	xi1	xi2	xi12	xi22	yi xi1	yi xi2	xi1xi2
1	14,4	4	154	16	23716	57,6	2217,6	616
2	16,9	2	155	4	24025	33,8	2619,5	310
3	13	5	149	25	22201	65	1937	745
4	9,6	7	128	49	16384	67,2	1228,8	896
5	9,8	7	134	49	17956	68,6	1313,2	938
6	9,6	7	127	49	16129	67,2	1219,2	889
7	16,8	2	157	4	24649	33,6	2637,6	314
8	14,8	4	160	16	25600	59,2	2368	640
9	9,8	7	134	49	17956	68,6	1313,2	938
10	16,9	2	154	4	23716	33,8	2602,6	308
11	16	3	161	9	25921	48	2576	483
12	17,4	2	167	4	27889	34,8	2905,8	334
13	17,2	2	163	4	26569	34,4	2803,6	326
14	17,4	2	163	4	26569	34,8	2836,2	326
15	15,7	3	155	9	24025	47,1	2433,5	465
16	17,1	2	162	4	26244	34,2	2770,2	324
Σ	232,4	61	2423	299	369549	787,9	35782	8852

---

Смотрите также файлы

• Индивидуальный социальный проект Цель изучение особенностей трудоустройства несовершеннолетних. Задачи.pptx

• Новый курс экономическая и социальная программа.docx

• Экономика Казахстана в годы войны. Оккупация гитлеровцами западных районов ссср привела к тому, что резко выросла значимость Сибири и Казахстана в экономике страны.docx

• Семиотика наука о знаковых системах.docx

• Сайт интернет реклама экономический.docx