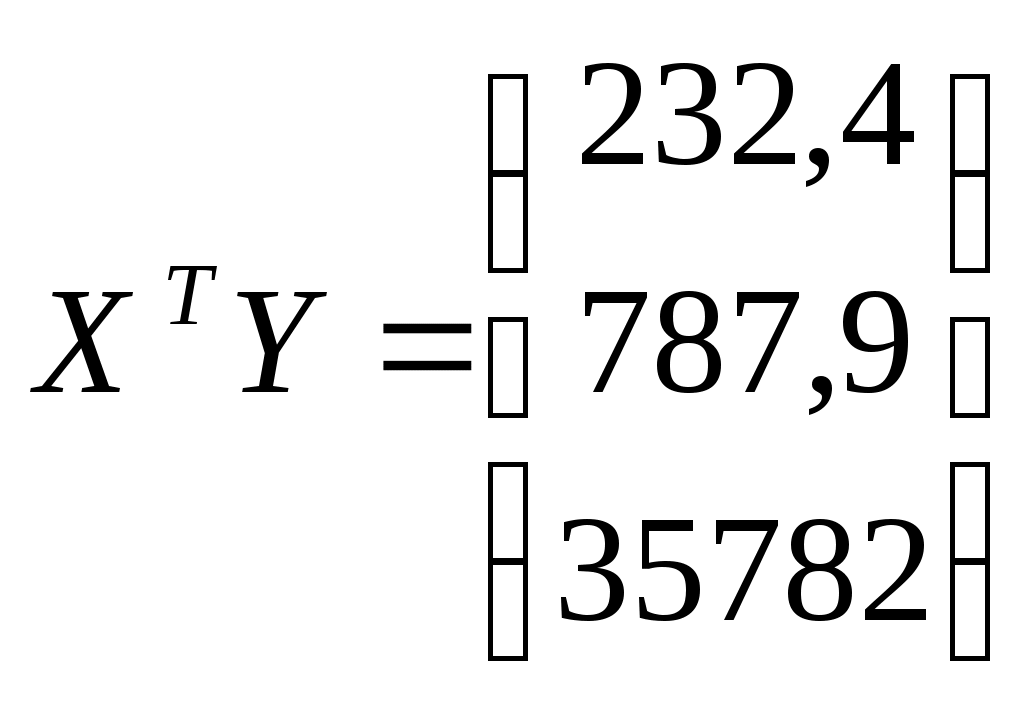
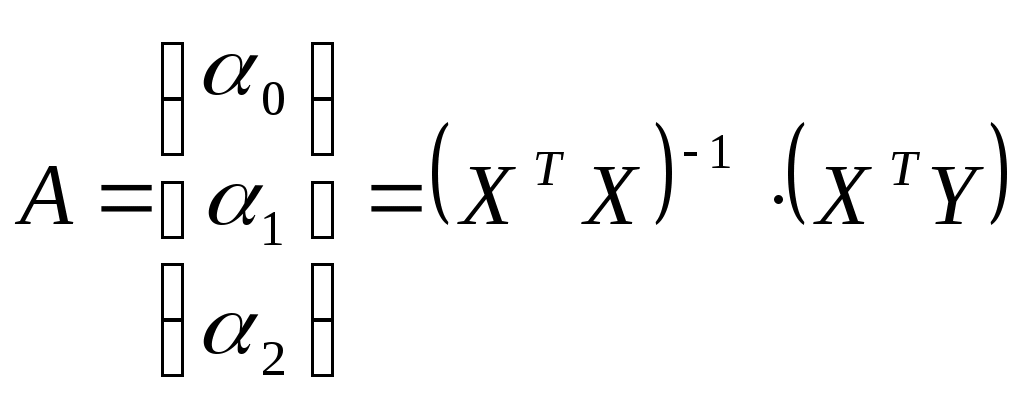
;



Найдем :



алгебраические дополнения:







Тогда обратная матрица

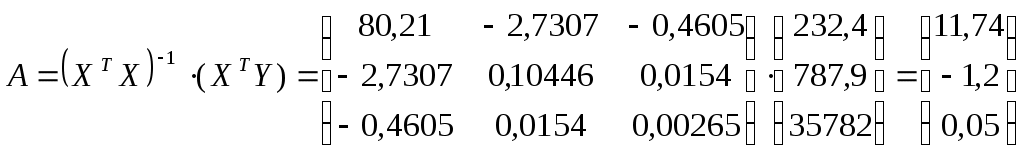таким образом, получаем уравнение регрессии:
.
2.2. Проверить статистическую значимость параметров и уравнения множественной регрессии с надежностью 0,9.
Для вычисления коэффициента детерминации составим таблицу: (таблица 7)

ỹi	ỹi -yi	(ỹi -yi )2
14,64	0,24	0,0576	0,015625
17,09	0,19	0,0361	5,640625
13,19	0,19	0,0361	2,325625
9,74	0,14	0,0196	24,25563
10,04	0,24	0,0576	22,32563
9,69	0,09	0,0081	24,25563
17,19	0,39	0,1521	5,175625
14,94	0,14	0,0196	0,075625
10,04	0,24	0,0576	22,32563
17,04	0,14	0,0196	5,640625
16,19	0,19	0,0361	2,175625
17,69	0,29	0,0841	8,265625
17,49	0,29	0,0841	7,155625
17,49	0,09	0,0081	8,265625
15,89	0,19	0,0361	1,380625
17,44	0,34	0,1156	6,630625
Σ		0,83	145,91

---

Коэффициент корреляции

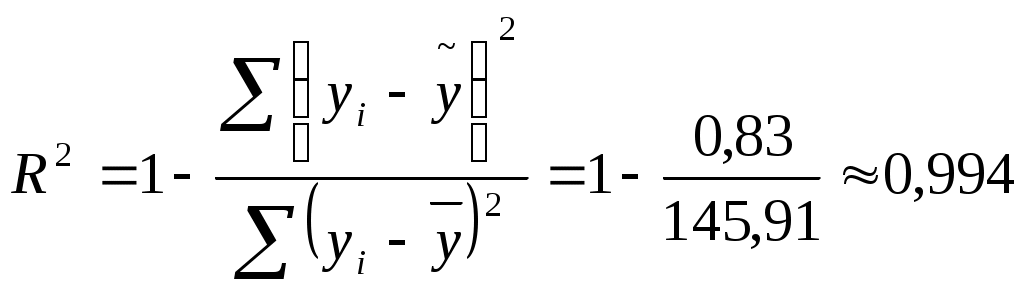
Следовательно, регрессия y на x₁ и x ₂ объясняет 99,4% колебаний значений у. Это свидетельствует о значительном суммарном влиянии независимых переменных x₁ и x ₂ на зависимую переменную у.

Качество уравнения множественной регрессии оценим с помощью F-теста, найдем



При уровне значимости 0,05 и табличное значение F_m=3,81. Неравенство F_mф выполняется, гипотеза о незначимости коэффициентов регрессии отклоняется и признается статистическая значимость уравнения регрессии.
2.3. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей возраста 3 года и мощностью 165 л.с. с доверительной вероятностью 0,9.
Точечный прогноз:

где - вектор независимых переменных, для которого определяется прогноз. В нашем случае

Тогда
Интервальный прогноз:

;

, где

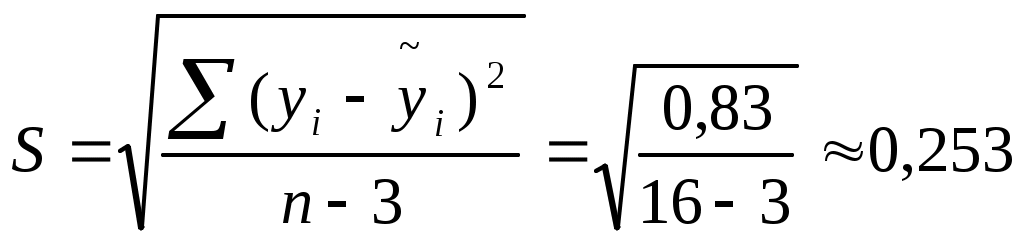
тогда




т.е. с надежностью 90% цена на поступившие автомобили попадет в интервал (16,15 ; 16,63).
3. Экономическая интерпретация.
Рассмотрим зависимость цены от возраста:

Так как = -0,9966 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии .

Коэффициент формально определяет цену нового автомобиля, т.е. когда .

Коэффициент характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста автомобиля на 1 год следует ожидать уменьшения цены на 1,48 тыс. у.е.

Зависимость цены от мощности:

Так как = 0,9516 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии .

Коэффициент характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении мощности автомобиля на 1 л.с следует ожидать увеличения цены на 0,22 тыс. у.е.
В результате исследования зависимости объема цены от двух факторов – возраста и мощности двигателя получено уравнение множественной регрессии

Коэффициент показывает, что при увеличении возраста на 1 год и неизменной мощности двигателя следует ожидать снижения цены автомобиля на 1,2 тыс. у.е.

Коэффициент показывает, что при увеличении мощности на 1 л.с и неизменном возрасте следует ожидать увеличения цены автомобиля на 0,05 тыс. у.е.

1   2   3   4

---

Задача 2

Временной ряд
В базе данных магазина также содержится информация об объеме ежемесячных продаж автомобилей за прошлый год, представленная в следующей таблице: (таблица 8)

месяц t	объем продаж, zt
1	229
2	207
3	217
4	257
5	272
6	298
7	313
8	324
9	286
10	314
11	344
12	318

1. 
   Представить графически ежемесячные объемы продаж автомагазина. На основе визуального анализа построенного графика выдвинуть гипотезу о виде статистической зависимости объема продаж от времени и записать ее математически.
   

Построим график ежемесячных продаж автомагазина:


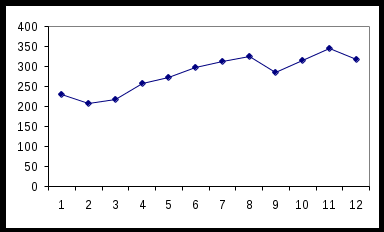
рис. 3 Траектория временного ряда
На основе визуального наблюдения ломанной линии динамики продаж можно выдвинуть гипотезу о наличии линейного тренда – устойчивого роста среднего уровня временного ряда.

Математически линейная зависимость выразится формулой , где - неизвестные параметры, - случайные возмущения.

2. 
   Методом наименьших квадратов найти оценку уравнения линейного тренда
   

---

Cоставим вспомогательную таблицу: (таблица 9)

	t	zt	ti2	zi ti
	1	229	1	229
	2	207	4	414
	3	217	9	651
	4	257	16	1028
	5	272	25	1360
	6	298	36	1788
	7	313	49	2191
	8	324	64	2592
	9	286	81	2574
	10	314	100	3140
	11	344	121	3784
	12	318	144	3816
Σ	78	3379	650	23567

т.к. n=12, то = = 281,58

= = 6,5

тогда


таким образом, получаем уравнение регрессии:


3. Для линии тренда построить доверительную полосу надежности 0,95. Нарисовать ее на графике вместе с линией тренда и исходным временным рядом.

---

Для расчета доверительных интервалов составим следующую таблицу: (таблица 10)

t	zt	Zt	zt -Zt	(zt -Zt )2	ti -tср	(ti -tср)2	Sz	Zн	Zв
1	229	219,87	9,13	83,3569	-5,5	30,25	11,6	194	245,74
2	207	231,09	-24,09	580,3281	-4,5	20,25	10,13	208,5	253,68
3	217	242,31	-25,31	640,5961	-3,5	12,25	8,78	222,73	261,89
4	257	253,53	3,47	12,0409	-2,5	6,25	7,61	236,56	270,5
5	272	264,75	7,25	52,5625	-1,5	2,25	6,72	249,76	279,74
6	298	275,97	22,03	485,3209	-0,5	0,25	6,23	262,08	289,86
7	313	287,19	25,81	666,1561	0,5	0,25	6,23	273,3	301,08
8	324	298,41	25,59	654,8481	1,5	2,25	6,72	283,42	313,4
9	286	309,63	-23,63	558,3769	2,5	6,25	7,61	292,66	326,6
10	314	320,85	-6,85	46,9225	3,5	12,25	8,78	301,27	340,43
11	344	332,07	11,93	142,3249	4,5	20,25	10,13	309,48	354,66
12	318	343,29	-25,29	639,5841	5,5	30,25	11,6	317,42	369,16
Σ				4562,418		143

---

Смотрите также файлы

• Индивидуальный социальный проект Цель изучение особенностей трудоустройства несовершеннолетних. Задачи.pptx

• Новый курс экономическая и социальная программа.docx

• Экономика Казахстана в годы войны. Оккупация гитлеровцами западных районов ссср привела к тому, что резко выросла значимость Сибири и Казахстана в экономике страны.docx

• Семиотика наука о знаковых системах.docx

• Сайт интернет реклама экономический.docx