Добавлен: 19.10.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| № п/п | Задача | Ответ |
| 1. | Рассчитать наибольшее и наименьшее значения функции на заданном отрезке: 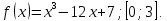 | 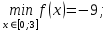 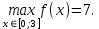 |
| 1) Найти первую производную и все критические точки | ||
| Подробное решение: 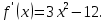 Для нахождения критических точек приравняем производную к нулю. 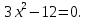 Решим уравнение. 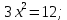 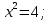 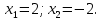 Получили две критические точки. Но только первая из них принадлежит отрезку 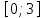 . . | ||
| 2) Вычислить значения функции в критических точках | ||
| Подробное решение: 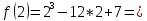 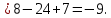 | ||
| 3)Вычислить значения функции на концах промежутка | ||
| Подробное решение: 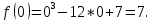 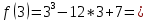 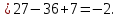 | ||
| 4)Сравнить все полученные значения функции и выбрать среди них самое большое и самое малое | ||
| Подробное решение: 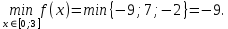 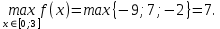 Наименьшее значение функция принимает в стационарной точке 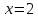 . .Наибольшее – на левом конце отрезка в точке 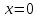 . . |
| № п/п | Задача |
| 2а. | Провести полное исследование и построить графики данных функций: а) 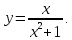 |
| Найти область определения функции, исследовать её поведение на границах этой области | |
| Подробное решение: Заданная по условию функция 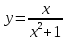 определена и непрерывна на всем множестве действительных чисел. определена и непрерывна на всем множестве действительных чисел.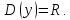 | |
| Найти точки разрыва и классифицировать их с помощью односторонних пределов | |
| Подробное решение: Так как исследуемая функция определена и непрерывна на всей числовой оси, то точек разрыва, а, следовательно, и вертикальных асимптот нет. | |
| Исследовать периодичность, чётность (нечётность) | |
| Подробное решение: Функция непериодична. 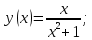 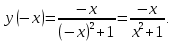 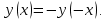 Следовательно, функция нечетная. |
| № п/п | Задача |
| 2а. | Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции |
| Подробное решение: Подставим  в выражение функции. в выражение функции.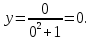 Получили, что график функции пересекает оси координат в точке (0;0). Чтобы найти промежутки знакопостоянства функции решим неравенства: 1) 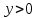 . .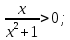 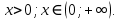 2) 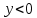 . .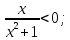 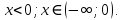 |
| № п/п | Задача |
| 2а. | Найти асимптоты |
| Подробное решение: Уже было выяснено, что вертикальных асимптот нет. Исследуем на наличие невертикальных асимптот. Для этого вычислим следующие пределы. 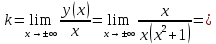 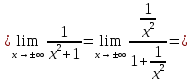 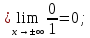 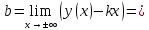 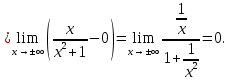 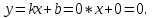 Оба предела существуют и не зависят от знака бесконечности. Следовательно, прямая 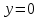 является двусторонней горизонтальной асимптотой. является двусторонней горизонтальной асимптотой. |
| № п/п | Задача |
| 2а. | Найти точки экстремума и интервалы монотонности |
| Подробное решение: Вычислим первую производную функции. 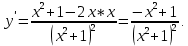 Приравняем производную к нулю. 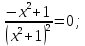 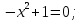 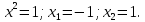 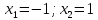 – критические точки. – критические точки. Составим таблицу изменений знака производной. 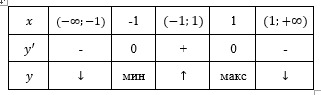 Так как производная на интервалах 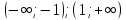 отрицательна, то функция здесь отрицательна, то функция здесь  убывает. Соответственно при положительном знаке производной на интервале убывает. Соответственно при положительном знаке производной на интервале 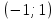 функция возрастает. При переходе через точку функция возрастает. При переходе через точку 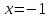 производная меняет свой знак с минуса на плюс, значит, это точка минимума. При переходе через точку производная меняет свой знак с минуса на плюс, значит, это точка минимума. При переходе через точку 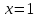 знак производной меняется с плюса на минус, следовательно, точка знак производной меняется с плюса на минус, следовательно, точка 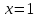 является максимумом. является максимумом. |
| № п/п | Задача |
| 2а. | Найти точки перегиба и интервалы выпуклости и вогнутости |
| Подробное решение: Интервалы выпуклости и вогнутости найдем по знаку производной второго порядка y′′. Найдем вторую производную и возможные точки перегиба. 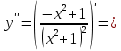 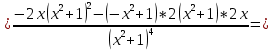 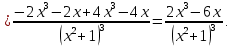 Приравняем вторую производную к нулю. 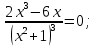 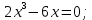 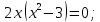 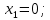 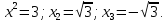 Получили три возможные точки перегиба. На интервале 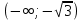 вторая производная имеет знак минус, следовательно, график здесь выпуклый. На интервале вторая производная имеет знак минус, следовательно, график здесь выпуклый. На интервале 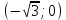 вторая производная положительна, значит график вогнутый. вторая производная положительна, значит график вогнутый.На интервале 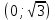 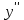 имеет знак минус, следовательно, график выпуклый. имеет знак минус, следовательно, график выпуклый.На интервале 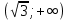 вторая производная положительна, значит график вогнутый. вторая производная положительна, значит график вогнутый.При переходе через каждую из трех точек направление выпуклости меняется на противоположное, следовательно, 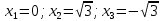 – точки перегиба. – точки перегиба. |
| № п/п | Задача |
| 2а. | Построить график, используя полученные результаты |
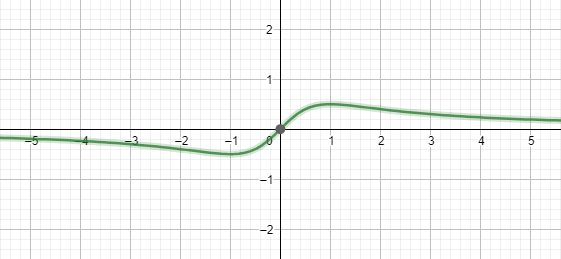 |
| № п/п | Задача |
| 2б. | Провести полное исследование и построить графики данных функций: б) 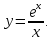 |
| Найти область определения функции, исследовать её поведение на границах этой области | |
| Подробное решение: Функция 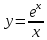 не определена в одной точке не определена в одной точке  . Следовательно, ее область определения имеет вид: . Следовательно, ее область определения имеет вид: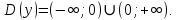 Найдем односторонние пределы функции в точке  . .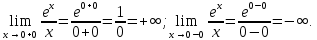 Так как односторонние пределы в точке  бесконечны, то прямая бесконечны, то прямая  является вертикальной асимптотой. является вертикальной асимптотой. | |
| Найти точки разрыва и классифицировать их с помощью односторонних пределов | |
| Подробное решение: Так как исследуемая функция в точке  не определена, то это точка разрыва функции. не определена, то это точка разрыва функции.Уже были найдены односторонние пределы функции в этой точке и равны бесконечности. Следовательно, это точка разрыва второго рода. | |
| Исследовать периодичность, чётность (нечётность) | |
| Подробное решение: Исследуемая функция непериодична. 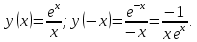 Значит, функция не является ни четной, ни нечетной. |
| № п/п | Задача |
| 2б. | Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции |
| Подробное решение: Уже было выяснено, что  – точка разрыва. Следовательно, ось Оу график функции не пересекает. – точка разрыва. Следовательно, ось Оу график функции не пересекает.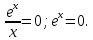 Уравнение не имеет решения. Следовательно, ось Оx график функции также не пересекает. Чтобы найти промежутки знакопостоянства функции решим неравенства: 1)  . .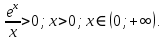 2) 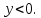 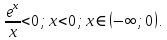 | |
| Найти асимптоты | |
| Подробное решение: Вертикальная асимптота  уже была найдена выше. уже была найдена выше. Исследуем на наличие невертикальных асимптот. Для этого вычислим предел. 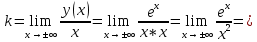 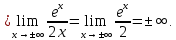 Так как не существует конечного пределы, но нет и наклонных асимптот. |
