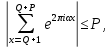ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ВВЕДЕНИЕ
Тригонометрическими суммами назывются суммы вида
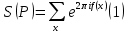 где суммирование распространено на все целые или часть целых из некоторого интервала, P-число слагаемых и f(x) – произвольная функция, принимающая при целых x действительные значения. К изучению таких сумм могут быть сведены многие вопросы теории чисел и ее приложений.
где суммирование распространено на все целые или часть целых из некоторого интервала, P-число слагаемых и f(x) – произвольная функция, принимающая при целых x действительные значения. К изучению таких сумм могут быть сведены многие вопросы теории чисел и ее приложений.Покажем, например, как возникают тригонометрические суммы при решении вопроса о возможности представить натуральное число N в виде суммы одинаковых степеней натуральных чисел
N =
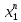 + ... +
+ ... + 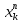 (2)
(2)(проблема Варинга ) . Пусть n , k и N – фиксированные натуральные числа , P – наибольшее целое, не превосходящее
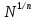 , и
, и 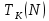 – число решений уравнения (2) . При целом
– число решений уравнения (2) . При целом 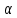 определим функцию
определим функцию 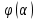 с помощью равенства
с помощью равенства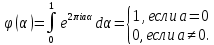
Тогда, очевидно ,
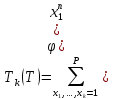
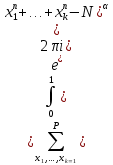
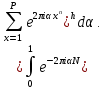
Таким образом, арифметическая задача о числе решений уравнения (2) сводится к исследованию интеграла, зависящего от степени тригонометрической суммы
 .
. Наиболее важны для приложений суммы, в которых функция f(x) является полиномом , а область суммирования предcтавляет собой некоторый интервал:
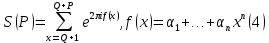
Такие тригонометрические суммы называются суммами Вейля, а степень полинома f(x) – степенью суммы Вейля . Так, например, сумма (3) , возникающая в проблеме Варинга , является суммой Вейля степени
n.
Центральной задачей теории тригонометрических сумм является получение возможно более точных верхних оценок для модуля тригонометрической суммы. Так как модуль каждого слагаемого суммы равен единице, то для всякой суммы (1) справедлива тривиальная оценка
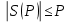 .
.Первые общие нетривиальные оценки сумм (4) принадлежат Г. Вейлю. При определеных требованиях к старшему коэффиценту полинома f(x) им было показано , что при любом
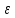 из интервала 0
из интервала 0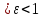 справедливо оценка
справедливо оценка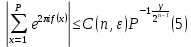
где
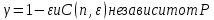 . Существенное усилиние этого результата при n
. Существенное усилиние этого результата при n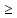 12 , было получено И. М. Виноградовым
12 , было получено И. М. Виноградовым 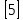 , показавшим, что в оценке (5) при некотором
, показавшим, что в оценке (5) при некотором 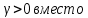 C(n,
C(n, 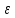 )
) можно поставить величину C(n)
можно поставить величину C(n)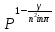 .
.Если дробные доли функции f(x) имеют целочисленный период, т.е. если при некотором натуральном
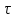 для всякого целого x выполняется равенство
для всякого целого x выполняется равенство  =
=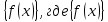 - дробная доля функции f(x), то
- дробная доля функции f(x), то сумма
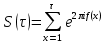
называется полной тригонометрической суммой. Примером полной тригонометрической суммы может служить сумма Вейля, в которой все коэффициенты полинома f(x) рациональны и число слагаемых равно общему знаменателю этих коэффициентов:
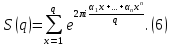
При
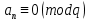 такие суммы называются польными рациональными суммами степени n
такие суммы называются польными рациональными суммами степени n
. Для них известны более точные оценки , чем оценки сумм Вейля оющего вида.
Всестороннее исследование полных рациональных сумм второй степени было проведено Гауссом. В частности , им было показано, что при (a,q)=1 для модуля суммы
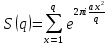
выполняется равенства
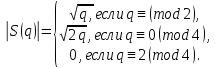
Для полных рациональных сумм произвольной степени при простом q Морделлом было получена оценка
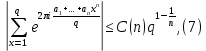
где C(n) не зависит от q . Хуа Ло-ген распространил эту оценку на случай произвольного натурального q. Существенное усиление результата Морделла было получено А. Вейлем, показавшим, что при простим q модуль суммы (7) не превосходит величины (n-1)
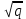 . При фиксированном n и возрастающем qоценки А. Вейля и Хуа Ло-гена является по порядку роста предельно точными и не допускают уже дальнейшего усиления.
. При фиксированном n и возрастающем qоценки А. Вейля и Хуа Ло-гена является по порядку роста предельно точными и не допускают уже дальнейшего усиления.Примером полных сумм, отличных от полных рациональных сумм (6), является тригонометрические суммы с показательной функцией
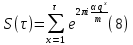
где ( q, m)=1 и
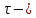 показатель, которому q принадлежит по модулю m. К оценкам таких сумм и сумм S(P) с
показатель, которому q принадлежит по модулю m. К оценкам таких сумм и сумм S(P) с 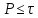 сводится вопрос о числе появлений фиксированной группы знаков среди первых P знаков периодической дроби, возникающей при записи произвольного рационального числа
сводится вопрос о числе появлений фиксированной группы знаков среди первых P знаков периодической дроби, возникающей при записи произвольного рационального числа 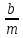 в q- ичной системе счисления. Величина суммы (8) зависит от характера разложения m на простые сомножители и для полных сумм в большинстве случаев оказывается равной нулю. Если же
в q- ичной системе счисления. Величина суммы (8) зависит от характера разложения m на простые сомножители и для полных сумм в большинстве случаев оказывается равной нулю. Если же 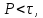 при
при 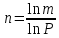 и m равном степени простого числа, выполняется оценка
и m равном степени простого числа, выполняется оценка 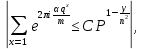
где C и
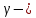 абсолютные константы.
абсолютные константы.
Необходимость оценивать тригонометрические суммы возникает и в вопросе о приближенном вычислении интегралов произвольной кратности . Рассмотрим, например, квадратную формулу, постренную с помощью произвольной сетки
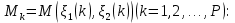
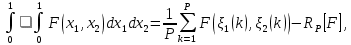 (9)
(9)где F(
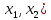 – периодическая функция, заданная абсолютно сходящимся рядмом Фурье:
– периодическая функция, заданная абсолютно сходящимся рядмом Фурье: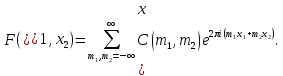
Подставляя этот ряд в равенство (9), после перемены порядка суммирования получим
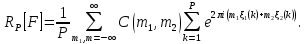
где
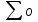 значает что суммирование по всем
значает что суммирование по всем 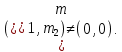
Отсюда следует, что для погрешности квадратурной формулы (9) выполняется оценка
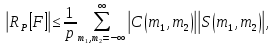
где тригонометрическая сумма

Определяется заданием сетки M
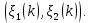 Выбирая функции
Выбирая функции 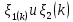 так, чтобы суммы S
так, чтобы суммы S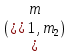 оценивались достаточно хорошо, мы получаем возможность строить квадратурные формулы высокой точности.
оценивались достаточно хорошо, мы получаем возможность строить квадратурные формулы высокой точности.Первая глава книги содержит подробное изложение начальных сведений из теории полных тригонометрических сумм и сумм, оценки которых сводятся к оценкам полных сумм. Теоремы, помещенные в этой главе, сравнительно просты, однако они составляют фундамент теории тригонометрических сумм общего вида и служат необходимой подготовкой к более сложным построениям второй главы. Для иллюстрации возможных приложений полных сумм в первой главе дано решение вопроса о распределении знаков в периоде систематических дробей, возникающих при записи рациональных чисел в произвольной системе счисления.
Вторая глава технически значительно сложнее первой. Она посвящена изложению теории сумм Вейля общего вида. Наряду с основополагающими методами Вейля и Виноградова в ней изложены исследования, основанные на повторном применении теоремы о среднем, и дано их приложение к оценкам сумм, возникающих в теории дзета-функции Римана

В третьей главе рассматриваются приложения тригонометрических сумм к распределению дробных долей и построению квадратурных формул. В ней изложена созданная Вейлем теория равномерного распределения, рассмотрены вопросы вполне равномерного распределения, и их связи с теорией нормальных чисел. Заключительная часть главы посвящено вопросу о приближенном вычислении кратных интегралов и построению интерполяционных формул для функций многих переменных

-
Суммы первой степени.
Простейшим примером сумм Вейля является сумма первой степени
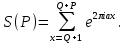
Это сумма относится к числу немногих тригонометрических сумм, которые удается не только оценить, но и непосредственно вычислить. Действительно, если ????- целое, то
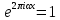 и , следовательно,
и , следовательно,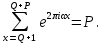
Если же ???? не является целым числом, то
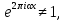 и ,
и ,геометрическую прогрессию, получим
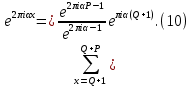
Однако обычно удобнее пользоваться не этими точными равенствами, а следующей оценкой:
1. Пусть ????-произвольное действительное число Q-целое и P-натуральное. Тогда
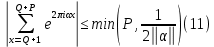
где
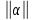 -расстояние от ???? до ближайшего целого.
-расстояние от ???? до ближайшего целого.Доказательство. Так как обе части (11) является четными периодическими функциями ???? с периодом, равным единице, то оценку (11) достаточно доказать при 0≤ ???? ≤
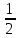 . Замечая, что на этом интервале
. Замечая, что на этом интервале ,
,при????≠0 из равенства (10) получим
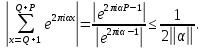
Пользуясь этой оценкой при
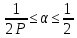 и применяя при
и применяя при 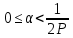 тривиальную оценку
тривиальную оценку