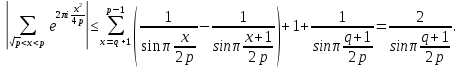ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Действительно, из полноты сумм (27) следует, что дробные доли функций
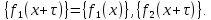
Но тогда
{
И сумма (28) будет полной тригонометрической суммой.
Теорема 1 (формула умножения). Пусть при целых
{f (х) }= {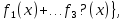
Где дробные доли функсий
Тогда справедливо равенство
Доказательство. Так как, согласно условию,
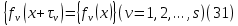
и в силу (29)
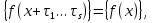
то все тригонометрические суммы в равенстве (30) являются полными. Пусть величины
независимо друг от друга пробегают полные системы вычетов соответственно по модулям 
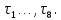При этом, так как 
попарно взаимно просты, сумма
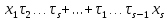
будет пробегать полную систему вычетов по модулю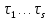
и следовательно,
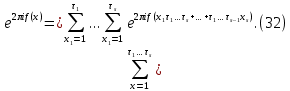
Так как в силу (29) и (31)
то равенство (23) можно переписать в виде
Отсюда, пользуясь свойством (25), получаем формулу умножения:
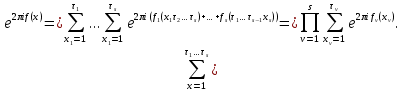
Формула умножения в ряде случаев существенно упрощает исследование полных сумм. Покажем этот на примере полных рациональных сумм.
Пусть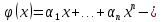
произвольный целочисленный полином
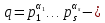каноническое разложение q на простые сомножители и числа 
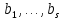выбраны так , чтобы выполнялось сравнение
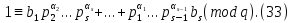
Тогда для полных рациональных сумм справедливо равенство
Действительно, так как
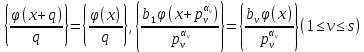и в силу (33)
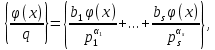
то применяя теорему 1, получаем равенство (34).
Формула умножения (34) сводит исследование полных рациональных сумм с произвольным знаменателем q к исследованию более простых сумм со знаменателем, равным степени простого числа.
В качестве другого примера на формулу умножения докажем равенство
Которое понадобится в дальнейшем при исследовании сумм Гаусса. Рассмотрим сумму
Выделим слагаемые, с х, кратным q, и объединим остальные слагаемые в четыре группы:
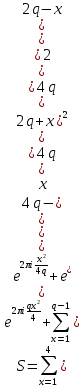
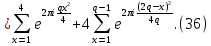
С другой стороны, согласно формуле умножения
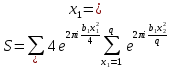
где
удовлетворяют сравнению 
Так как это сравнение выполняется при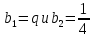 
(1−
то после выделение слагаемого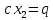 
и замены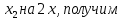 
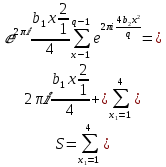
Теперь, замечая, что
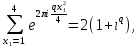
Из (36) и (37) получаем равенство (35):
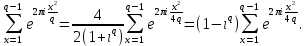
Рассмотрим теперь некоторый класс тригонометрических сумм, нетривиальные оценки которых можно легко получить путем сведения задачи к оценке полных сумм.
Пусть дробные доли функции f(x) периодичны, их наименьший период равен τ, 1≤P<τ и Q- произвольное целое. Тогда сумма
называется неполной тригонометрической суммой.
Теорема 2. Для всякой неполной тригонометрической суммы S(P), определенной равенством (38), выполняется оценка
Доказательство. Из свойства (14) функции
следует, что при P≤????
Применяя этот разрывный множитель и пользуясь леммой 2, получим
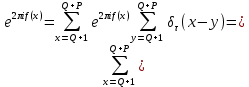
Так как дробные доли функций f(x) и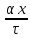
имеют период ????, то согласно (28) последнаяя сумма в этом равенстве является полной и, следовательно,
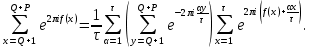
Отсюда, пользуясь леммами 1 и 3 , получаем утверждение теоремы:
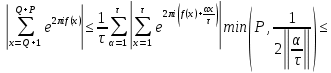
Суммой Гаусса называется полная рациональная тригонометрическая сумма второй степени
где q- произвольное натуральное число и (????, q)=1. Суммы Гаусса, так же как и рассмотренные и первом параграфе суммы первой степени, можно точно вычислить. Рассмотрим сперва сравнительно простой вопрос о вычислении модуля таких сумм.
Теорема 3. Для модуля суммы Гаусса выполняется равенство
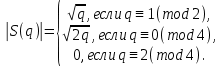
Доказательство. Обозначим через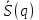
сумму, сопряженную сумме S(q). Тогда получим
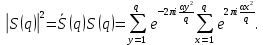
Воспользуемся вторым свойством полных сумм и заменим во внутренней сумме x на x+ y. Тогда, после перемены порядка суммирования, получим
Отсюда согласно лемме 2 следует, что
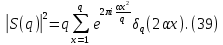
Так как по условию
???? и y взаимно просты, то при нечетном q в первой части этого равенства отлично от нуля только то слагаемого, которое получается при x=q, и, следовательно,
Если же q четно, то в сумме (39) отличны от нуля два слагаемых, которые получается при
Поэтому, замечая что при четном q из (????,q)=1 следует нечетность а получим
Отсюда и из равенства (40) следует утверждение теоремы.
Заметим, что в случае нечетного q утверждение теоремы 3 справедливо и для сумм общего вида.
Действительно, покажем, что при
выполняется равенство
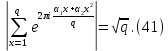
Выберем b так, чтобы выполнялось сравнение
Тогда очевидно,
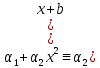
и, следовательно,
Отсюда получаем равенство (41):
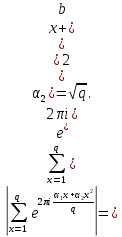
Рассмотрим простейшие свойства сумм Гаусса. Будем предполагать, что q=p, где p>2-простое число. Легко показать, что при ????≡0(mod p) справедливо равенство
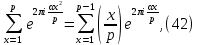
где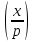
- символ Лежандра. Действительно, если x изменяется от 1 до p-1, то 
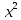дважды пробегает значения квадратичных вычетов по модулю p, и так как
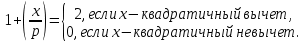
то
Отсюда, замечая, что согласно лемме 2 при ????≢0(modp)
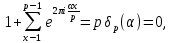
получаем равенство (42).
Покажем теперь, что при ????≢0(modp)
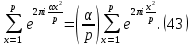Действительно, умножая равенство (42) на 
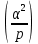=1 и замечая, что
????x пробегает приведенную систему вычетов одновременно с x, получим
Отсюда, так как в силу (42)
следует равенство (43).
Покажем еще, что зная модуль суммы Гаусса, легко вычислить ее значение с точностью до знака. Действительно, пусть
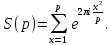
Тогда, пользуясь равенством (43), получим
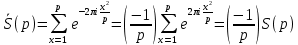
Отсюда после умножения на
следует, что
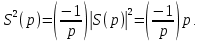
Теперь, так как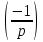
принимает значение 1 при p≡1(mod 4) и значение -1 при p≡3(mod 4), получаем
Вопрос о том, какой знак следует выбрать в этих равенствах, более сложен. Его решение было найдено Гауссом. Ниже приведено сравнительно простое доказательство теоремы Гаусса, предложенное в работе
Теорема 4. При любом нечетном простом p выполняется равенства
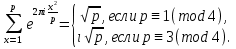
Доказательство. Покажем сначала, что
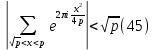
Действительно применим преобразования Абеля
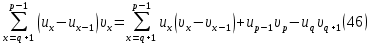
пр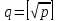и
и
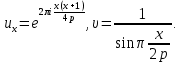
Так как, очевидно,
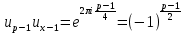
и
то из (46) следует, что
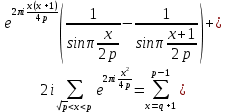
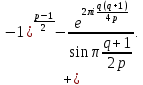
Но тогда, замечая, что при 1≤ x≤ p−1
получим
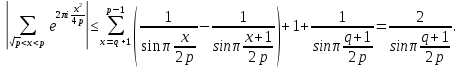
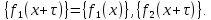
Но тогда
{
И сумма (28) будет полной тригонометрической суммой.
Теорема 1 (формула умножения). Пусть при целых
{f (х) }= {
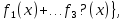
Где дробные доли функсий
Тогда справедливо равенство
Доказательство. Так как, согласно условию,
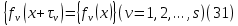
и в силу (29)
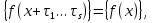
то все тригонометрические суммы в равенстве (30) являются полными. Пусть величины
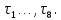независимо друг от друга пробегают полные системы вычетов соответственно по модулям При этом, так как попарно взаимно просты, сумма 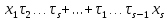будет пробегать полную систему вычетов по модулю
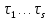и следовательно,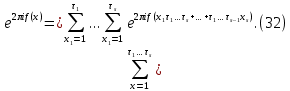 Так как в силу (29) и (31)
то равенство (23) можно переписать в виде
Отсюда, пользуясь свойством (25), получаем формулу умножения:
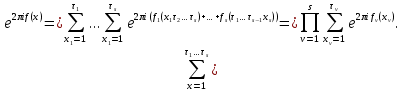
Формула умножения в ряде случаев существенно упрощает исследование полных сумм. Покажем этот на примере полных рациональных сумм.
Пусть
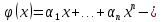произвольный целочисленный полином 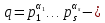каноническое разложение q на простые сомножители и числа 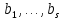выбраны так , чтобы выполнялось сравнение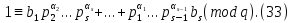
Тогда для полных рациональных сумм справедливо равенство
Действительно, так как
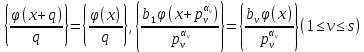и в силу (33)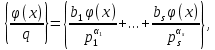 то применяя теорему 1, получаем равенство (34).
Формула умножения (34) сводит исследование полных рациональных сумм с произвольным знаменателем q к исследованию более простых сумм со знаменателем, равным степени простого числа.
В качестве другого примера на формулу умножения докажем равенство
Которое понадобится в дальнейшем при исследовании сумм Гаусса. Рассмотрим сумму
Выделим слагаемые, с х, кратным q, и объединим остальные слагаемые в четыре группы:
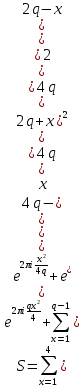
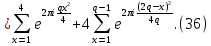
С другой стороны, согласно формуле умножения
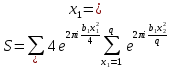
где
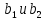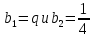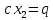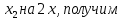
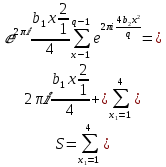
удовлетворяют сравнению Так как это сравнение выполняется при (1− то после выделение слагаемого и замены Теперь, замечая, что
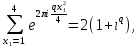
Из (36) и (37) получаем равенство (35):
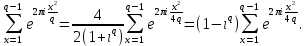
Рассмотрим теперь некоторый класс тригонометрических сумм, нетривиальные оценки которых можно легко получить путем сведения задачи к оценке полных сумм.
Пусть дробные доли функции f(x) периодичны, их наименьший период равен τ, 1≤P<τ и Q- произвольное целое. Тогда сумма
называется неполной тригонометрической суммой.
Теорема 2. Для всякой неполной тригонометрической суммы S(P), определенной равенством (38), выполняется оценка
Доказательство. Из свойства (14) функции
следует, что при P≤???? Применяя этот разрывный множитель и пользуясь леммой 2, получим
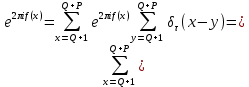
Так как дробные доли функций f(x) и
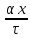имеют период ????, то согласно (28) последнаяя сумма в этом равенстве является полной и, следовательно,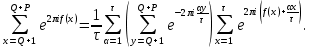 Отсюда, пользуясь леммами 1 и 3 , получаем утверждение теоремы:
-
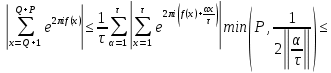
Суммы Гаусса
Суммой Гаусса называется полная рациональная тригонометрическая сумма второй степени
где q- произвольное натуральное число и (????, q)=1. Суммы Гаусса, так же как и рассмотренные и первом параграфе суммы первой степени, можно точно вычислить. Рассмотрим сперва сравнительно простой вопрос о вычислении модуля таких сумм.
Теорема 3. Для модуля суммы Гаусса выполняется равенство
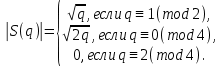
Доказательство. Обозначим через
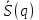сумму, сопряженную сумме S(q). Тогда получим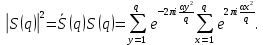 Воспользуемся вторым свойством полных сумм и заменим во внутренней сумме x на x+ y. Тогда, после перемены порядка суммирования, получим
Отсюда согласно лемме 2 следует, что
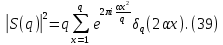
Так как по условию
???? и y взаимно просты, то при нечетном q в первой части этого равенства отлично от нуля только то слагаемого, которое получается при x=q, и, следовательно,
Если же q четно, то в сумме (39) отличны от нуля два слагаемых, которые получается при
Поэтому, замечая что при четном q из (????,q)=1 следует нечетность а получим Отсюда и из равенства (40) следует утверждение теоремы.
Заметим, что в случае нечетного q утверждение теоремы 3 справедливо и для сумм общего вида.
Действительно, покажем, что при
выполняется равенство 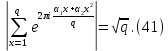Выберем b так, чтобы выполнялось сравнение
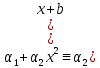
Тогда очевидно, и, следовательно,
Отсюда получаем равенство (41):
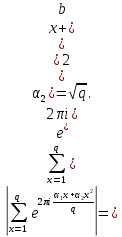
Рассмотрим простейшие свойства сумм Гаусса. Будем предполагать, что q=p, где p>2-простое число. Легко показать, что при ????≡0(mod p) справедливо равенство
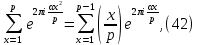
где
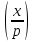- символ Лежандра. Действительно, если x изменяется от 1 до p-1, то 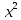дважды пробегает значения квадратичных вычетов по модулю p, и так как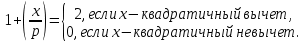 то
Отсюда, замечая, что согласно лемме 2 при ????≢0(modp)
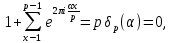
получаем равенство (42).
Покажем теперь, что при ????≢0(modp)
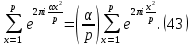Действительно, умножая равенство (42) на 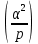=1 и замечая, что
????x пробегает приведенную систему вычетов одновременно с x, получим
Отсюда, так как в силу (42)
следует равенство (43).
Покажем еще, что зная модуль суммы Гаусса, легко вычислить ее значение с точностью до знака. Действительно, пусть
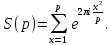
Тогда, пользуясь равенством (43), получим
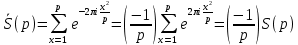
Отсюда после умножения на
следует, что 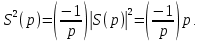Теперь, так как
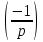принимает значение 1 при p≡1(mod 4) и значение -1 при p≡3(mod 4), получаем Вопрос о том, какой знак следует выбрать в этих равенствах, более сложен. Его решение было найдено Гауссом. Ниже приведено сравнительно простое доказательство теоремы Гаусса, предложенное в работе
Теорема 4. При любом нечетном простом p выполняется равенства
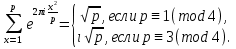
Доказательство. Покажем сначала, что
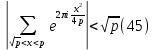
Действительно применим преобразования Абеля
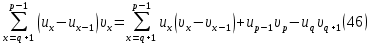
пр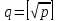и
и 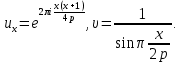Так как, очевидно,
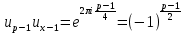
и
то из (46) следует, что
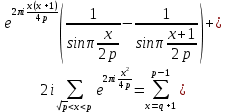
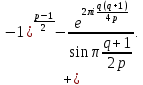
Но тогда, замечая, что при 1≤ x≤ p−1
получим