ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 22
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
получаем утверждение леммы.
Пусть ????-произвольное целое и q-натуральное. Определим функцию
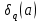
c помощью равенства
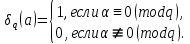
В следующей лемме устанавливается связь между этой функцией и полными рациональными суммами первой степени.
Лемма 2. При любом целом а и любом натуральном q выполняется равенство
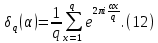
Доказательство. Если α≡0 (mod q), то
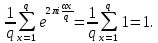
Пусть теперь α≠0 (mod q). Тогда получим
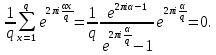
Утверждение леммы следует, очевидно, из этих равенств и определения
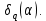
Функция
постоянно будет использоваться в дальнейшем изложении. Ее значение определяется тем, что она позволяет устанавливать связь между исследованием тригонометрических сумм и вопросом о числе решений сравнений.Рассмотрим, например, вопрос о числе решений сравнения
(13)аналогичный упомянутому во введении вопросу о числе решений уравнения Варинге (2). Обозначим через T(
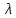) число решений этого сравнения, когда величины 
независимо друг от друга пробегают полные системы вычетов по модулю q. Очевидно, в силу определения функции ,
Отсюда, согласно лемме 2, следует, что
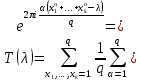
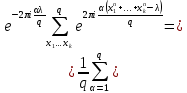
Таким образом, число решений сравнения (13) выражено через полные рациональные тригонометрические суммы
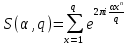
Приведем некоторые свойства функции
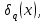непосредственно следующие из ее определения.1°. Функции
периодично. Ее период равен q.2°. Если (a , q)=1 и b- произвольное целое, то справедливы равенства
3°. При любом натуральном
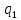выполняется равенства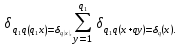
4°. Если
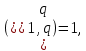справедливо равенство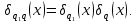
5°. При любом натуральном P, не превосходящем q, будет
Лемма 3. Пусть q-произвольное натуральное, 1≤α
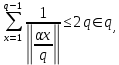
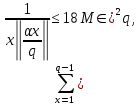
где М- наибольшее из неполных частных числа
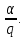
Доказательство. Пусть m- произвольное натуральное число. Пользуясь при x≥1 неравенством
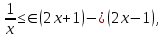
получим
Отсюда соответственно при нечетном и при четном q cледует, что
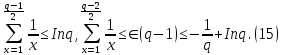
Так как функция
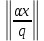периодично с периодом q и 
то при нечетном q согласно (15) получим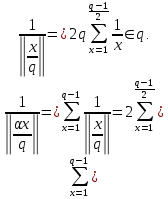 
Такая же оценка получается в силу (15) и при четном q:
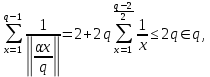чем доказано первое утверждение леммы. Для доказательства второго утверждения применим преобразование Абеля
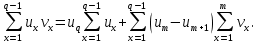
При
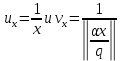получим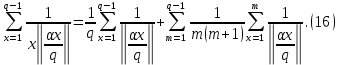 
Пусть разложение числа a/q в ценную дробь имеет вид
+ 
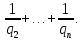
Тогда при
выполняются равенства 
(17)где
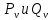взаимно просты,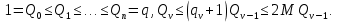 
Если
то , определяя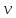 
из условия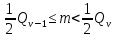 
и пользуясь равенством (17), получим
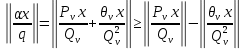. (18)Так как при
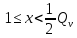будет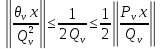
то из (18) следует, что
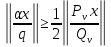.Но тогда, пользуясь первым неравенством леммы, получим
Если же
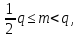то
и, следовательно оценка (19) выполняется не только при
но при любом m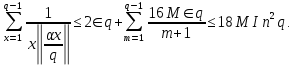
Покажем, что леммы, содержащие еще совсем небольшую информацию о тригонометрических суммах, позволяют получать нетривиальные арифметические результаты.
Пусть
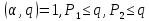и T-число решений сравнения
Если
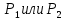совпадает с q, то, очевидно,
Вопрос становится сложнее, если и
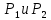меньше чем q. В этом случае можно показать, что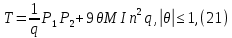 
где М-наибольшее из неполных частных разложения
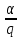в ценную дробь.Действительно, пользуясь леммой 2, получим
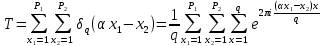
Отсюда после выделения слагаемого с x=q следует, что
где
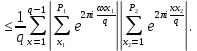
Таким образом вопрос о числе решений сравнения (20) сводится к вопросу об оценке сумм Вейля первой степени. Пользуясь леммой 1 и замечая, что
и
- четные периодические функции с периодом q, получим 
Отсюда согласно лемме 3 следует, что
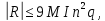
а это оценка в силу (22) равносильно равенству (21).
-
Общие свойства полных сумм
Как уже было сказано, сумма
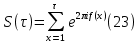
называется полной тригонометрической суммой, если при любом целом х для дробный долей функции f(x) выполняется равенство
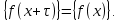
Приведем некоторые примеры полных сумм. Пусть
- целые и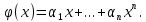 
Так как, очевидно, 
то выполняются сравнения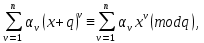 
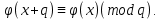
Но тогда при любом целом x
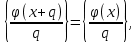
и, следовательно сумма
названная во введении полной рациональной суммой, будет полной тригонометрической суммой в смысле определения(23).
Рассмотрим теперь тригонометрическую сумму с показательной функцией
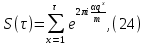
где (α,m)=1, (q,m)=1 и τ-показатель, которому q принадлежит по модулю m. Будем под
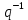понимать решение сравнения qx≡1(mod m), при любом целом x получим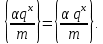 
Следовательно, τ является периодом дробных долей 2∗
функции
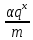и сумма (24) будет полной тригонометрической суммой.Приведем некоторые свойства полных сумм, непосредственно следующие из определения.
1°. Величина полной тригонометрической суммы (23) не изменится, если переменная суммирования вместе интервала
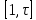будет пробегать любую полную систему вычетов по модулю τ.Действительно, так как
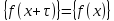, то при x ≡ y (mod τ) выполняется равенство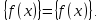 
Ну тогда
И совокупность слагаемых в сумме (23) не будет зависеть от того, образующие по модулю
полную систему вычетов, пробегает переменная суммирования.2
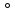. Если (
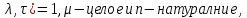то для полных сумм выполняются равенства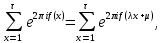 
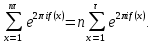
Первое из этих равенств является частным случаем свойства 1
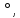так как при (
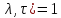линейная функция 
одновременно с х пробегает полную систему вычетов по модулю .3
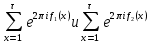
являются полными, то полной будет и сумма
