Отсюда, так как





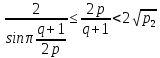
следует оценка (45).

Теперь, замечая, что

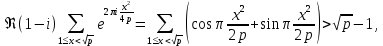и пользуясь оценкой (45), получим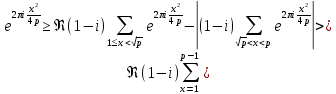





Пусть p≡1(mod 4). Тогда согласно (44),





т.е. эта сумма является действительным числом, и , следовательно,



Так как , согласно (35) при p≡1(mod 4)




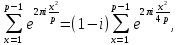
то, пользуясь оценкой (47), получим




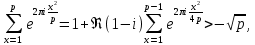
чем в силу (48) доказано первое утверждение теоремы.

Если p≡3(mod 4), то и согласно (35) и (44)



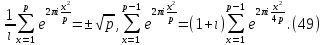
и, как и выше , получим



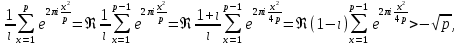
чем в силу первого из равенств (49) теорема доказана полностью.

Заметим, что утверждение теоремы 4 можно записать с помощью одного равенств, не выделяя особо случаи p≡1(mod 4) и p≡3(mod 4):



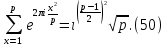
Отсюда в силу (43) при любом α≢0(mod p) получаем



Равенство (50) доказано в предположении, что p-простое нечетное число. Покажем, что такое же равенство справедливо и для сумм Гаусса с произвольным нечетным знаменателем q:



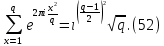
Рассмотрим сначала суммы вида




где ????-натуральное, p-нечетное простое и ???? взаимно простое с p. Пользуясь индукцией по ????, легко показать, что




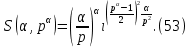
Действительно, при ????=1 это равенство совпадает с равенством (51). При ????=2 оно принимает вид 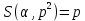и получается с помощью замены переменной суммирования:

---

Пусть равенство (53) доказано для некоторого ????≥2 и всех меньших значений ????. Докажем его для ????+1.

Очевидно



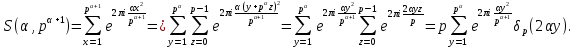
Замечая, что в последний сумме отличны от нуля только слагаемые с y, кратным p, и что 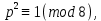получим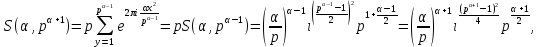



чем равенство (53) доказано полностью.

Пусть теперь q>1- произвольное нечетное число. Запишем каноническое разложение q в виде 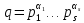и определим из сравнения


Будем считать, что в произведении нечетные степени простых стоит на первых r местах. Так как равенство (53) можно записать в виде



то, пользуясь формулой умножения (34), получим



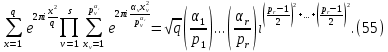
Из определения (54) следует, что



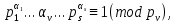
и, так как



то очевидно, при 1<v≤r






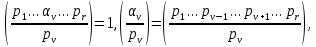
Определим величины 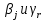равенствами




Тогда, пользуясь законом взаимности квадратичных вычетов в форме



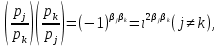
из (55) и (56) получим






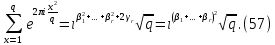
Так как, очевидно,




то из (57) следует, что для всякое нечетного q выполняется равенство (52):

---

Точное значение сумм Гаусса известно и для произвольное четного q. Если q≡2(mod 4), то согласно теорема 3 сумма Гаусса обращается в нуль. При q≡0(mod 4) можно показать, что



Таким образом полное описание величины сумм Гаусса дается равенствами

4. 
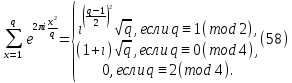
   Простейшие полные суммы
   

Естественным обобщением сумм Гаусса являются полные рациональные суммы вида




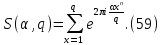
где α и q взаимно просты и n≥2. В отличие от сумм Гаусса (n=2) при n 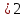для сумм (59) уже не удается получить явное выражение, но для них легко установить оценки , порядок которых не допускает дальнейшего улучшения. Совсем просто получается оценка





где p-простое число .

Действительно, пусть, соответственно, T(b) и T- число решений сравнений 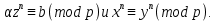Пользуясь свойствами двучленных сравнений, получим

T(b)≤d, T=1+d(p-1). (61)

где d=(n, p-1). С другой стороны, согласно лемме 2,



Следовательно, в силу (61),



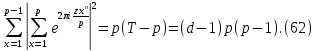
Так как согласно (25) при 1≤z≤p-1



то, проводя суммирование по z, получим,



Объединим здесь слагаемые с 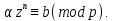Тогда, пользуясь оценкой (61) и равенством (62), получим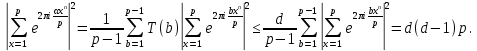

---

Лемма 1.






Пусть (a, D)=1. Тогда:




Доказательство:




По свойству модуля комплексного числа :
Имеем:




Сделаем замену x = x + t . Когда х и х пробегают полную систему вычетов по модулю D , от х и t пробегают независимо полные системы вычетов по модулю D.

Действительно, пусть х и х пробегают полную систему вычетов по модулю D . Тогда х = qD + k k=0, 1, …, D-1 , q є Z

х = pD + i i=0, 1, …, D-1 , p є Z

Следовательно, t = x – x = (q – p)D + (k – i) = l D + m , где m=0, 1, …, D-1 , l є Z




а) Пусть D – нечетное, т.е. (2а, D)=1




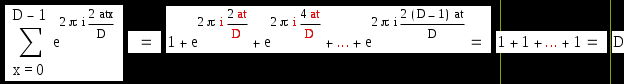
если D делит t.







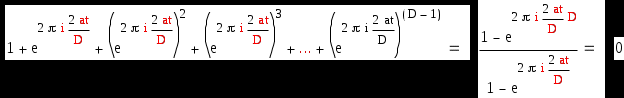
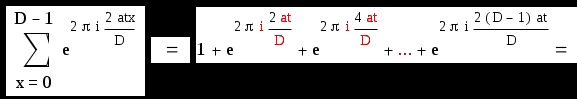
Если же D не делит t, то последнюю сумму можно записать в виде :




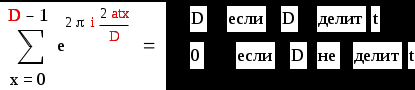
Получили :

Тогда




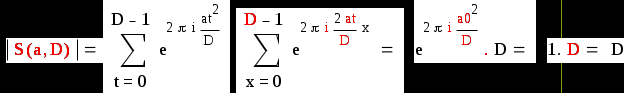
Отсюда




б) Пусть D делится на 4, т.е. возможно представление : D = 2D , где D – четное и ( a, D )=1 .

---

Получим :







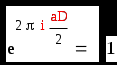
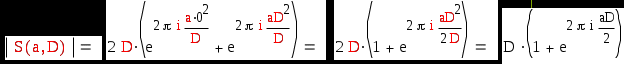
Так как D четное, то




Следовательно

в) Пусть D = 2 (mod 4) , т.е. D = 4q + 2 , q є Z




Тогда из предыдущего случая имеем : D = 2 (2q+1)= 2D , D - нечетное. Имеем :







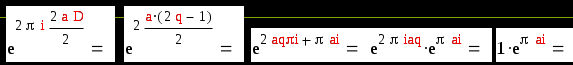
Что и требовалось.

Лемма 2.

Если D и D взаимно простые числа, то




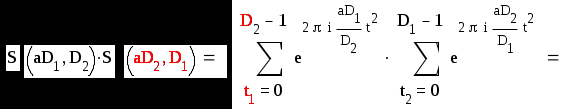
S ( aD₁ , D₂ ) S ( aD₂ , D₁ ) = S ( a , D₁ D₂ )



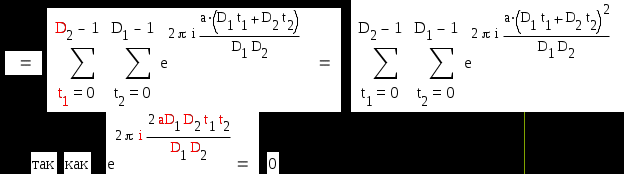
Доказательство:

В этих суммах t₁ пробегает полную систему вычетов по модулю D₂ , а t₂ пробегает полную систему вычетов по модулю D_2. При этом D₁t₁ + D₂t₂ пробегает полную систему вычетов по модулю D₁D₂ . Действительно , всего членов в сумме D₁D₂ и никакие два несравнимы между собой. Действительно, предположим противное : пусть D₁t₁ + D₂t₂ = D₁t₁ + D₂t₂ ( mod D₁D₂ )

Отсюда D₁ (t₁ – t

---

Смотрите также файлы

• Бюрократические и адаптивные организационные структуры.doc

• Лекция 1 Содержание Общие положение и понятия Основные радиокомпоненты электронных устройств.doc

• Основы противодействия терроризму и экстремизму.pptx

• Контрольная работа по геометрии в 7 классе по теме Смежные и вертикальные углы.docx

• Закон от 06. 12. 2011 402фз О бухгалтерском учете.docx