Кроме того, следует знать, что горизонтальные поверхности, перпендикулярные вектору силы тяжести, не параллельны между собой (они сжимаются у полюса) и поэтому высоты точек, лежащих на некоторой уровенной поверхности, уменьшаются по мере приближения к полюсу. Это уменьшение выражается формулой

,

где  разность широт точек, выраженная в радианной мере.

Например, воды озера Байкал, расположенные на средней широте _ср=53,5, с размахом широт 4,3 и средней высотой H=450 м на севере и юге отличаются по высоте на 0,2 м.

Превышением называется разность высот двух точек. На небольшой территории (в несколько десятков квадратных километров) величина h не зависит от принятой системы высот, получается, что

.

Понятие о равноугольной проекции Гаусса-Крюгера и общегосударственной системе плоских прямоугольных координат
Самостоятельное изучение.

Литература: Лекции по инженерной геодезии (с фрагментами методического комплекса). Учебное пособие/ В.П. Абрамов; под редакцией О.С. Разумова. – Тула, 2005. С 8–9.

Лекция 2.

Ориентирование линий. Прямая и обратная

геодезические задачи
Ориентировать линию местности – значит определять ее направление относительно некоторого другого направления, принятого за исходное. В геодезии в качестве исходного принимаются направления: 1) истинного меридиана; 2) магнитного меридиана; 3) оси абсцисс или линии, ей параллельной. В этой связи различают три вида ориентирных углов для одной и той же линии.

А 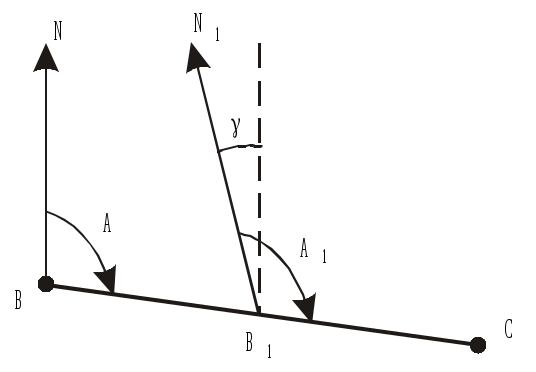строномический (истинный) азимут – горизонтальный угол А, отсчитанный в начальной точке линии по ходу часовой стрелки от северного направления истинного меридиана этой точки до заданного направления линии (рис.1.10). Угол А может принимать значения от 0 до 360.

А
Рис.1.10. Истинный азимут
зимут линии в разных ее точках меняется на угол  между направлением меридианов в этих точках. Этот угол называют сближением меридианов и, как следует из рис.1.10,

---

А₁=А+. Истинный азимут может быть определен на местности из астрономических наблюдений или при помощи гироскопического теодолита.

Для каждой линии принято различать прямые и обратные направления. Они отличаются друг от друга на 180 и угол  сближения меридианов, то есть

. (12)

Сам угол равен , (13)

где  – разность долгот точек;  – средняя широта.

Магнитный азимут – горизонтальный угол A_m, отсчитанный в начальной точке линии от северного направления магнитного меридиана (магнитной стрелки) по направлению движения часовой стрелки до направления заданной линии.A_m может быть измерен на местности с помощью буссоли (компаса).

Д 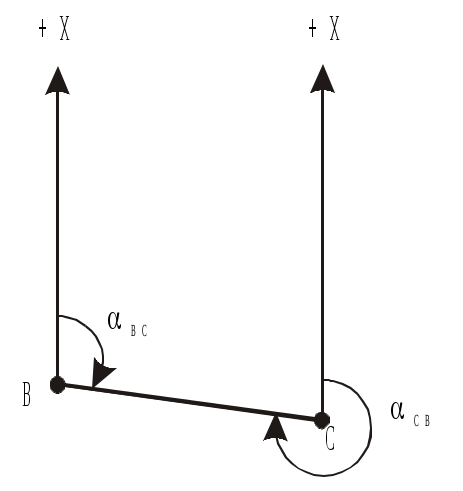ирекционный угол  отсчитывается от положительного направления оси абсцисс или линии, ей параллельной, по ходу часовой стрелки до заданного направления (рис.1.11). Прямой и обратный дирекционные углы отличаются друг от друга на 180, то есть

. (14)

О
Рис.1.11. Прямой и обратный

дирекционные углы
риентирные углы связаны друг с другом определенными соотношениями. Так, отклонение северного конца магнитной стрелки от направления истинного меридиана называется склонением  магнитной стрелки. Эта величина зависит от состояния магнитного поля Земли, которое непостоянно во времени. В районах магнитных аномалий значение  может изменяться в значительных пределах и ориентирование по магнитному азимуту там ненадежно.

Условно принято считать восточное склонение положительным, а западное отрицательным.

На рис.1.12 показано восточное склонение +, и в общем случае связь между истинным и магнитным азимутом выражается формулой

, (15)

(в формулу (15)  входит со своим знаком).

Угол , на который отклоняется в данной точке линия, параллельная оси абсцисс, от направления истинного меридиана, называется Гауссовым сближением меридианов.

---

Как было сказано выше, в проекции Гаусса–Крюгера за ось абсцисс принимается осевой меридиан зоны, поэтому для точки с известными географическими координатами  и  Гауссово сближение меридианов может быть вычислено по формуле

, (16)

где _N – долгота осевого меридиана зоны (10).

Т
Рис.1.12. Связь между ориентирными углами


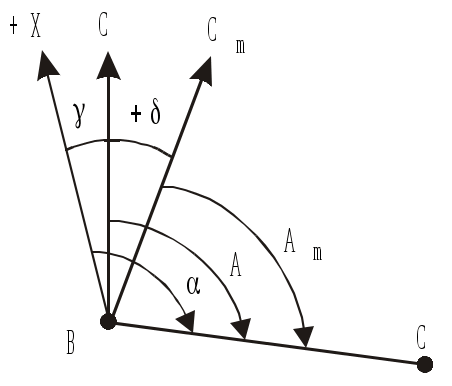
аким образом, для точек, лежащих к востоку от осевого меридиана, сближение меридиана положительное, а западное сближение отрицательное. На осевом меридиане и экваторе =0. Связь между истинным азимутом А и дирекционным углом  выражается соотношением

(17)

(формула имеет алгебраический смысл).

Н а топографических картах под южной рамкой обычно указывается среднее значение склонения магнитной стрелки и Гауссова сближения меридианов.

Д
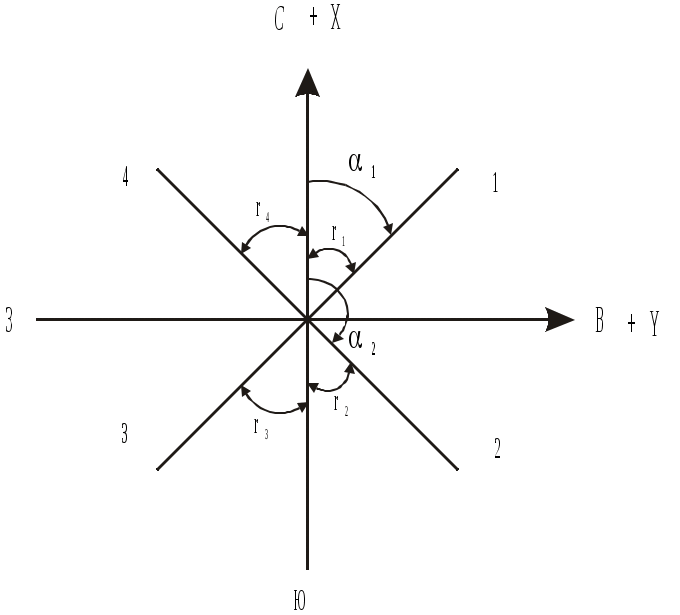
Рис.1.13. Румбы
ля ориентирования линий используют еще один ориентирный угол – румб (рис.1.13). Это острый горизонтальный угол rмежду ближайшим концом меридиана (или оси абсцисс) и направлением данной линии. Перед численным значением румба указывают его направление относительно сторон света. Связь между азимутами (дирекционными углами) и румбами показана в табл.1.1.
Таблица 1.1

Связь между румбами и дирекционными углами

Четверть	А (или )	Румб r
1	0 – 90	СВ: r1=1
2	90 – 180	ЮВ: r2=180-2
3	180 – 270	ЮЗ: r3=3-180
4	270 – 360	СЗ: r4=360-4

Прямая геодезическая задача состоит в вычислении координат точки 2 при известных координатах точки 1, расстоянию S₁₂ и дирекционному углу линии 1-2 (рис.1.14).
Из треугольника 1С2 следует:

,

---

,

где х₁₂ и х₁₂ – приращения координат.

Поэтому

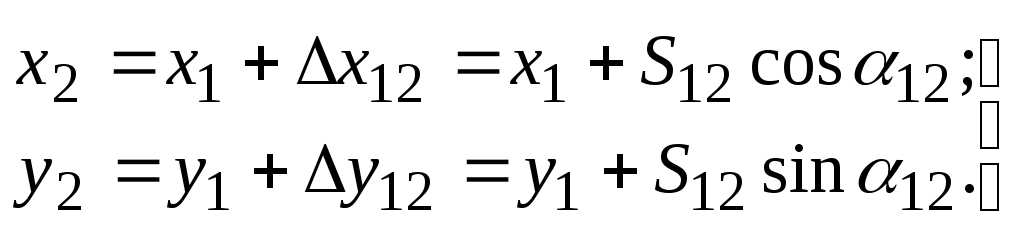(18)

З 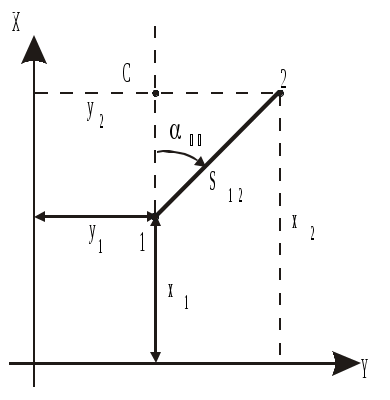наки у приращений координат определяются знаками тригонометрических функций cos и sin.

Обратная геодезическая задача заключается в определении длины линии Sи ее дирекционного угла  по координатам концов этой линии, то есть в задаче дано x₁, y₁, x₂, y₂. Требуется вычислить ₁₂ и S₁₂. Из треугольника 1С2 (см. рис.1.14) следует, что


Рис.1.14. Прямая геодезическая задача
, (19)

. (20)

При решении этой задачи на калькуляторе по команде arctg на табло высвечивается значение румба данной линии в градусах и долях градуса. В соответствии со знаками приращений координат (знаки cos и sin) нужно по табл.1.2 определить номер четверти, в которой проходит линия, и от румба перейти к дирекционному углу (см. табл.1.1), выразив его в градусах, минутах и секундах дуги.
Таблица 1.2

Четверть	x (cos)	y (sin)
1	+	+
2	-	+
3	-	-
4	+	-

Изображение рельефа на планах и картах
Рельефом называют совокупность неровностей местности естественного происхождения. На топографических картах рельеф обозначают с помощью горизонталей. Горизонталь – это непрерывная кривая линия, соединяющая точки местности, лежащие на одной высоте. Каждую горизонталь можно представить как след сечения рельефа местности уровенной поверхностью. Обычно такие сечения выполняют через определенный интервал по высоте h, который называется высотой сечения рельефа. Высоты горизонталей H отсчитывают от исходной (нулевой) уровенной поверхности, и они везде кратны

---

h. Расстояние между горизонталями в плане называют заложением a, оно на плане уменьшается по мере увеличения крутизны склона.

Р
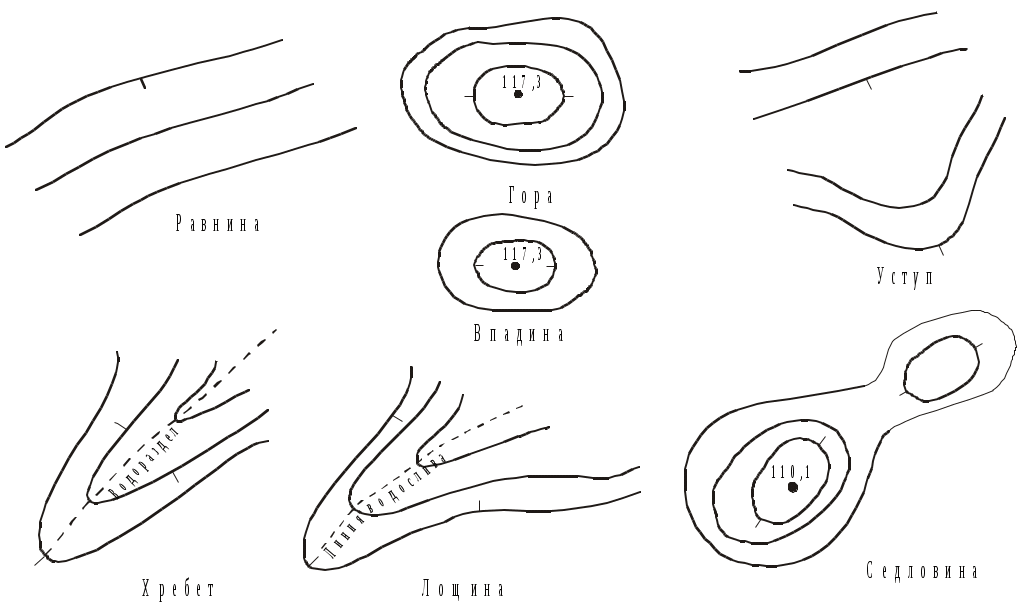
азличают следующие формы рельефа: равнина, гора (холм), впадина (котловина), хребет, лощина, седловина, уступ (терраса) (рис.1.15).

О
Рис.1.15. Основные формы рельефа



Рис.1.16. Условные знаки рельефа


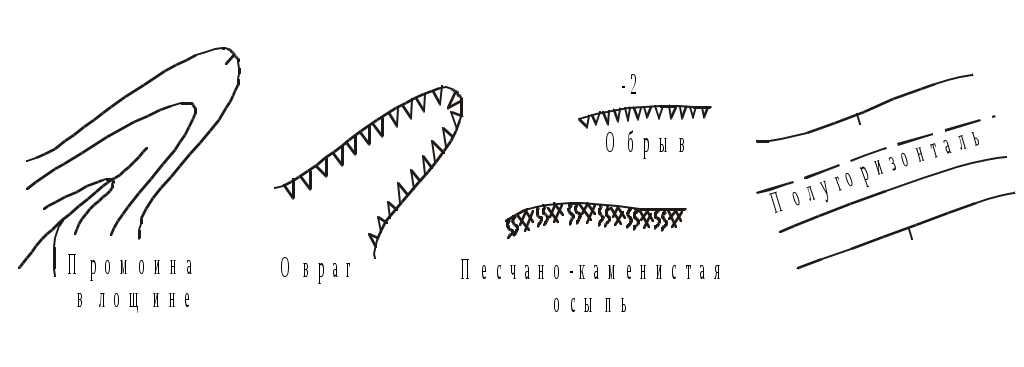
севая линия, соединяющая самые высокие точки хребта, называется линией водораздела. А осевая линия лощины, по которой стекает вода, называется тальвегом (линией водослива). На горизонталях ставят бергштрихи по направлению падения склона.

Свойства горизонталей:

1. Они соединяют точки местности, лежащие на одной высоте.

2. Они не пересекаются и не раздваиваются.

3. Их высоты всегда кратны высоте сечения рельефа h.

4. При заданной высоте сечения hрасстояния между горизонталями уменьшаются по мере увеличения крутизны склона.

5. Линии водораздела и водослива горизонтали пересекают под прямым углом.

Недостатки горизонталей:

1. Они не обладают наглядностью при изображении рельефа.

2. С их помощью нельзя изобразить любую форму рельефа (идеальную равнину, крутые и нависающие склоны, обрывы и др.).

3. При заданной высоте сечения рельефа его мелкие формы (меньше высоты h) не фиксируются на планах.

С учетом этих особенностей при изображении оврагов, промоин или обрывов используют специальные условные знаки (рис.1.16), а для картирования слабо выраженного рельефа проводят дополнительные прерывистые горизонтали через половину или четверть высоты сечения (полугоризонтали или четвертьгоризонтали).




Рис.1.17. Определение высот горизонталей




Для определения высоты Н горизонтали по отметке ближайшей к ней точки нужно знать высоту h сечения рельефа. Предположим, что на рис.1.17 h=5 м. На этом рисунке вершина горы расположена на высоте 117,3 м. Отметка ближайшей к ней горизонтали будет равна H=115 м, так как это число кратно высоте сечения и является ближайшим числом, меньшим отметки вершины 117,3 м.

В котловине ближайшая к точке дна горизонталь имеет отметку 120 м  это число кратно пяти метрам и больше отметки дна. На ровном склоне верхняя горизонталь имеет отметку 125 м, нижняя – 120 м. Если же одна из горизонталей снабжена отметкой (само число пишется так, чтобы верх цифры был обращен к вершине), то отметки соседних горизонталей можно определить, сообразуясь с высотой сечения рельефа и направлением бергштрихов.

---

Смотрите также файлы

• Памятка для учащихся и родителей.docx

• Урок литературного чтения Составила учитель начальных классов.ppt

• Кафедра математики, информатики и методики преподавания.docx

• Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное.docx

• Виды игр и их роль в развитии, обучении и воспитании детей Классификация игр.pptx