Файл: Лекции по инженерной геодезии для заочной форм обучения направлений 270100 Строительство, 270200 Транспортное строительство.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 61
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3=64˚ 30΄, то 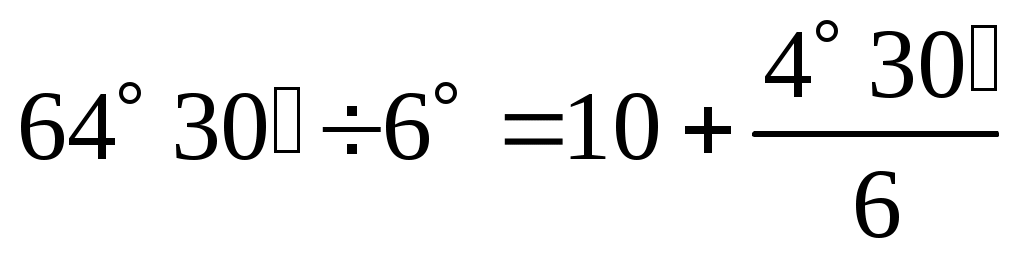 , и это значит, что до данной карты прошло 10 зон, а наша карта расположена в 11-й зоне. Кроме того, номер зоны равен уменьшенному на 30 номеру меридианальной колонны из номенклатуры. Так, если карта имеет номенклатуру R-38-56, то номер зоны равен 38-30=8. Наконец, номер зоны подписывается перед значением ординат вертикальных линий, подписанных на прямоугольной координатной сетке карты.
, и это значит, что до данной карты прошло 10 зон, а наша карта расположена в 11-й зоне. Кроме того, номер зоны равен уменьшенному на 30 номеру меридианальной колонны из номенклатуры. Так, если карта имеет номенклатуру R-38-56, то номер зоны равен 38-30=8. Наконец, номер зоны подписывается перед значением ординат вертикальных линий, подписанных на прямоугольной координатной сетке карты.
Интервал сетки прямоугольных координат на картах масштаба 1:10000 1:100000 бывает равным 1 км или 2 км. Целое число километров абсцисс и ординат подписывается за внутренней рамкой карты у горизонтальных и вертикальных линий этой сетки.
Высота сечения рельефа подписывается под южной рамкой карты; там же может быть показан график заложений для определения крутизны скатов по расстояниям между горизонталями.
Величины магнитного склонения и сближения меридианов указаны у южной рамки карты. Там же дается схематичный чертеж взаимного расположения основных ориентирных линий – истинного и магнитного меридианов и оси абсцисс (см. рис.1.12).
Измерение площадей фигур
Существуют три способа измерения площадей на картах: графический, аналитический и механический.
П
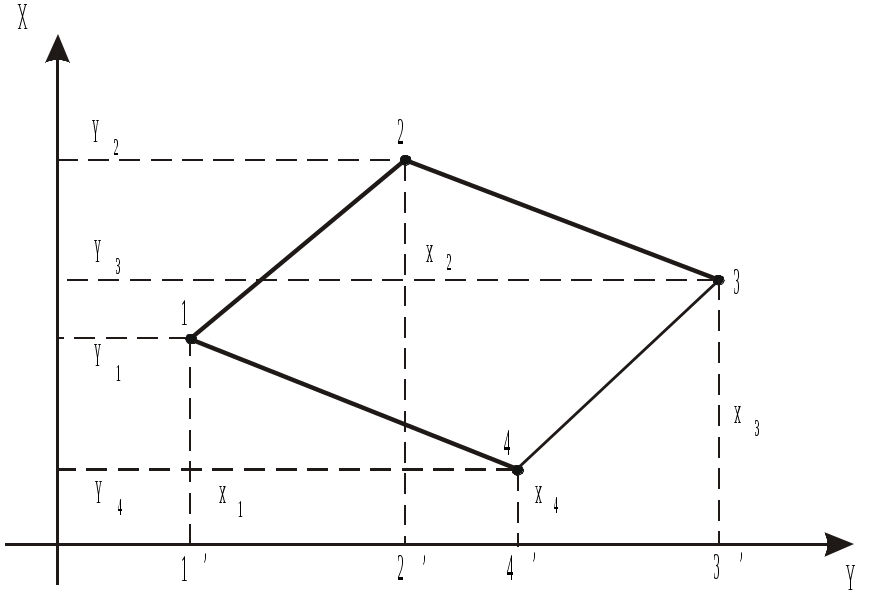
Рис.1.29. Определение площади по
координатам вершин
ри графическом способеизмеряемый контур разбивается на ряд геометрических фигур, с помощью поперечного масштаба измеряются их элементы и вычисляются площади, которые затем суммируются. Второй вариант графического способа предусматривает использование палетки – сетки квадратов, нанесенной на лист прозрачной бумаги. Зная площадь каждого квадрата в масштабе карты, подсчитывают число полных квадратов, покрывающих заданный контур, а из неполных на глаз составляют полные. Затем все числа складывают.
Аналитический способпредназначен для определения площадей многоугольников по координатам их вершин.
На рис.1.29 искомую площадь многоугольника P1234 можно представить как функцию площадей прямоугольных трапеций: P1234=P1’122’+P2’233’-P4’433’-P1’144’.
Основания каждой трапеции здесь равны абсциссам X
точек, а высота – разностям ординат Y.
Поэтому
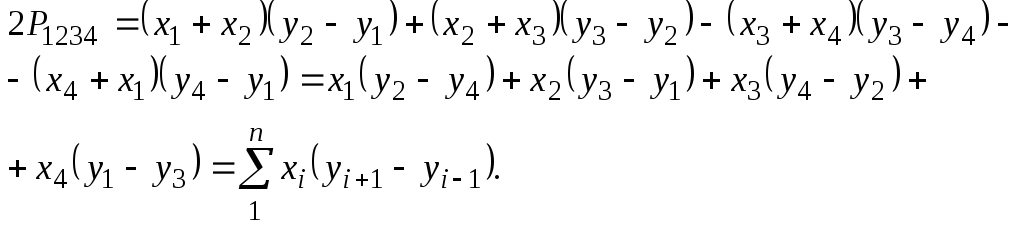 (27)
(27)
М
Рис.1.30. Схема планиметра
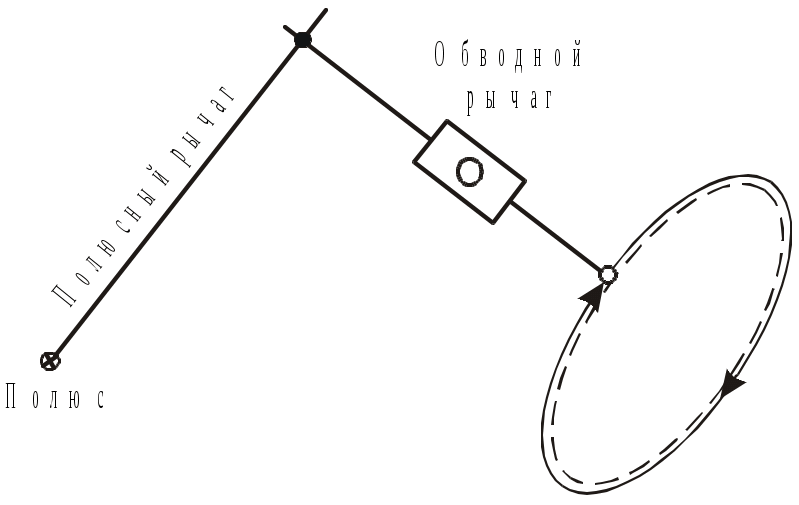 еханический способпредполагает использование специального прибора для измерения площадей – планиметра. Современный полярный планиметр состоит из двух рычагов – полюсного и обводного (рис.1.30, 1.31), которые соединяются шарнирно. На обводном рычаге расположен счетный механизм, а на конце рычага – обводной шпиль или прозрачная марка с точкой, которой обводится контур. Для измерения площади небольших фигур полюс устанавливают вне фигуры с таким расчетом, чтобы при обводе контура углы α между полюсным и обводным рычагами находились в пределах 30˚≤α≤150˚.
еханический способпредполагает использование специального прибора для измерения площадей – планиметра. Современный полярный планиметр состоит из двух рычагов – полюсного и обводного (рис.1.30, 1.31), которые соединяются шарнирно. На обводном рычаге расположен счетный механизм, а на конце рычага – обводной шпиль или прозрачная марка с точкой, которой обводится контур. Для измерения площади небольших фигур полюс устанавливают вне фигуры с таким расчетом, чтобы при обводе контура углы α между полюсным и обводным рычагами находились в пределах 30˚≤α≤150˚.
Для измерения площади до начала обвода марка (обводной шпиль) устанавливается на контур фигуры и снимается начальный отсчет n1. Этот отсчет состоит из числа полных оборотов диска (снимается по циферблату), числа целых делений барабана, прошедших до нуля верньера (две цифры), и долей деления, снимаемых по совпадающему штриху нониуса (верньера).
Так, отсчет на рис.1.31 n=6458.
После обвода фигуры и возвращения в начальную точку снимается второй отсчет n2. Площадь фигуры в делениях планиметра P=(n2-n1) делений. Если известна цена одного деления планиметра μ (в квадратных метрах или гектарах), то искомая площадь составит
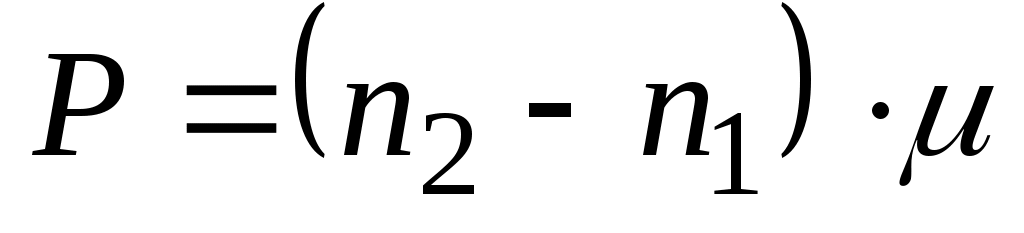 . (28)
. (28)
Для определения цены деления планиметра необходимо измерить этим прибором площадь какой-либо фигуры с известными размерами и площадью P0 (например, один или несколько квадратов координатной сетки). Тогда
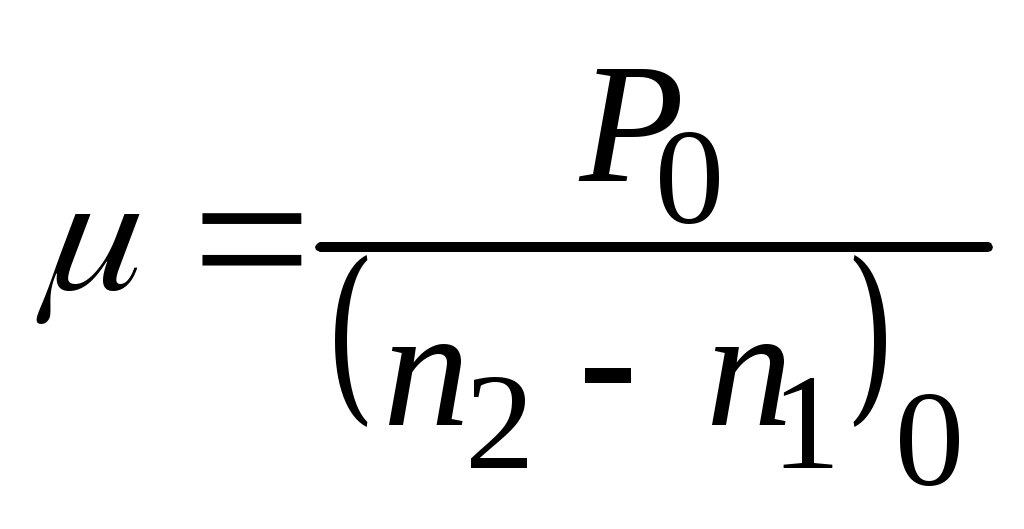 . (29)
. (29)
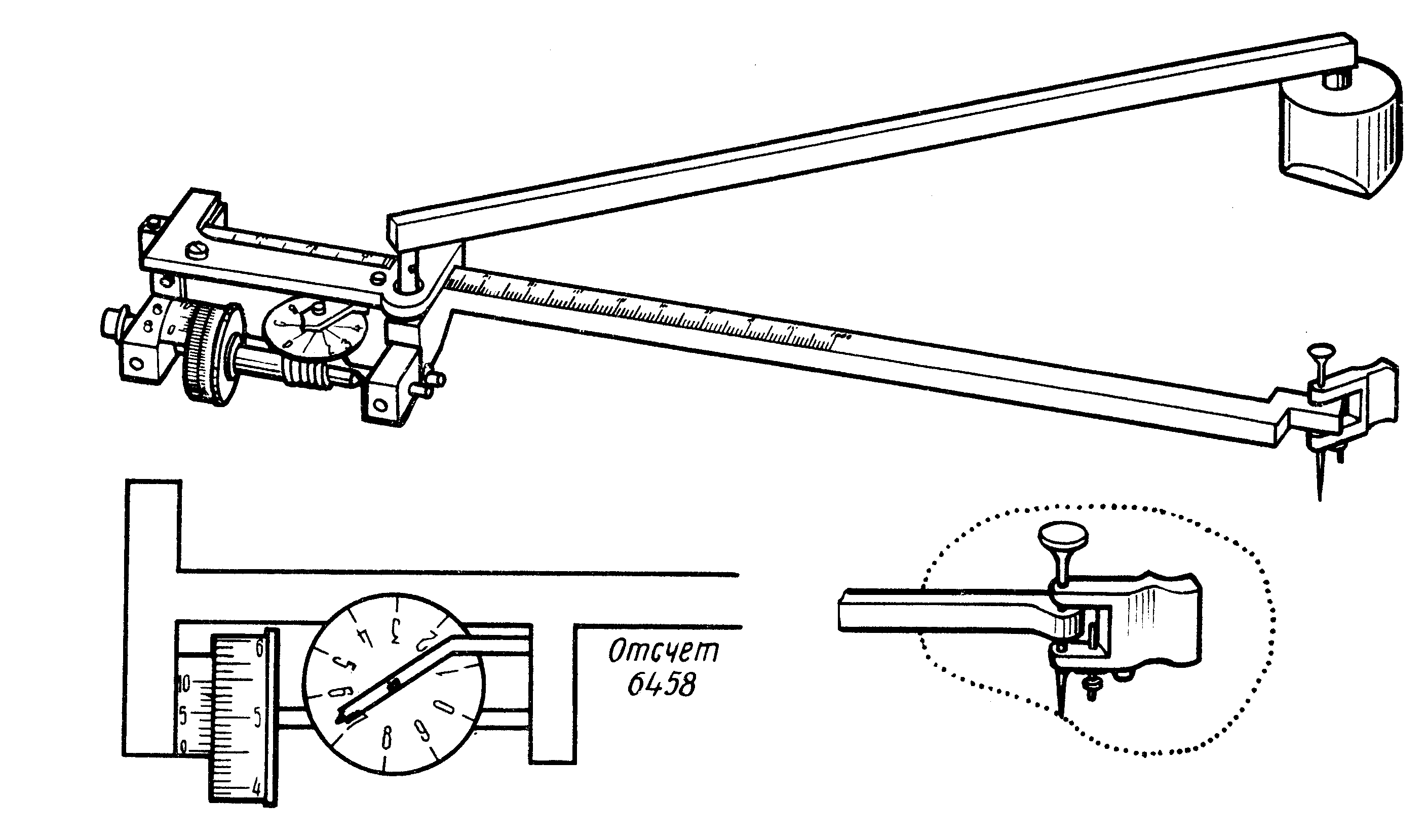
Рис.1.31. Планиметр
В целях контроля и повышения точности площадь фигуры измеряют несколько раз.
Если измеряемый участок велик, то полюс планиметра ставят внутри фигуры. Тогда
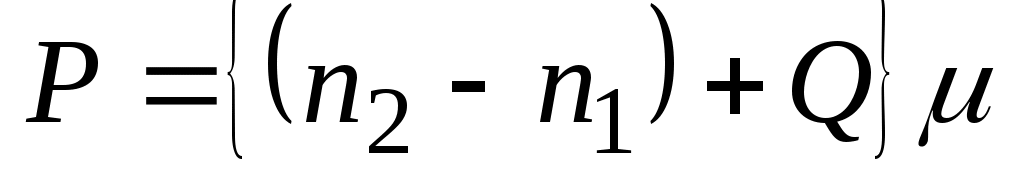 . (30)
. (30)
Для определения постоянного числа Qнеобходимо и достаточно измерить площадь одного и того же участка с полюсом вне фигуры и внутри фигуры. Если при этом получена разность отчетов
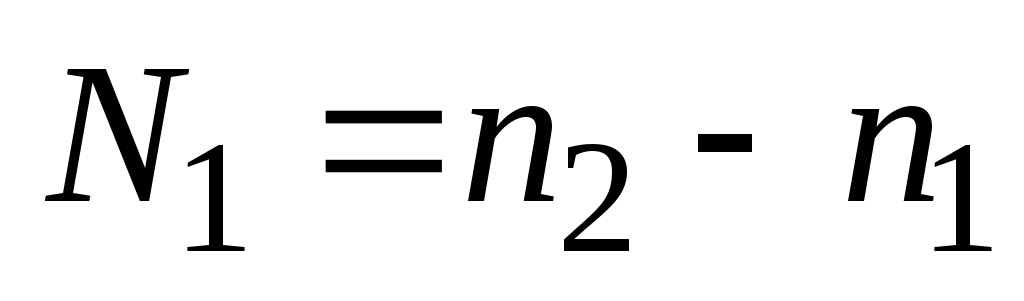 и
и 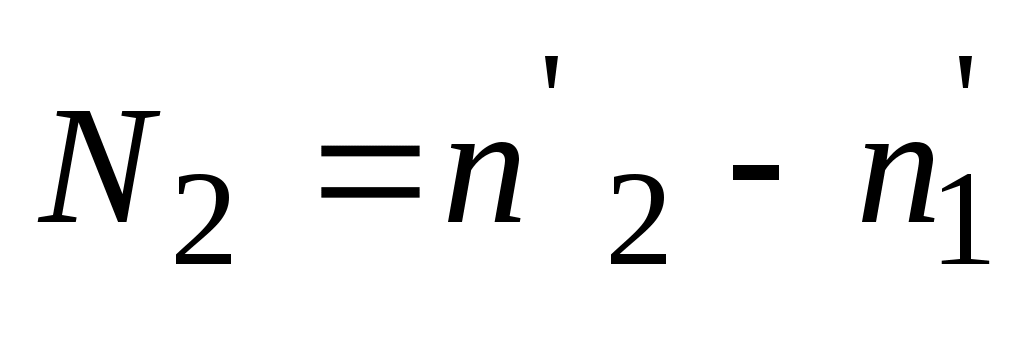 , то площадь P равна
, то площадь P равна 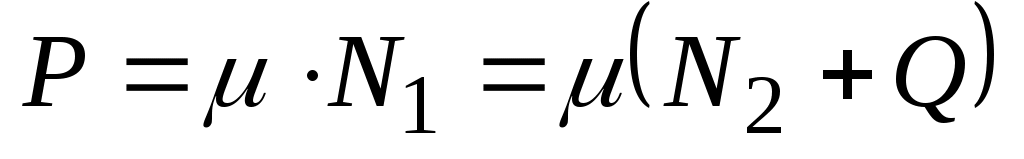 , откуда
, откуда
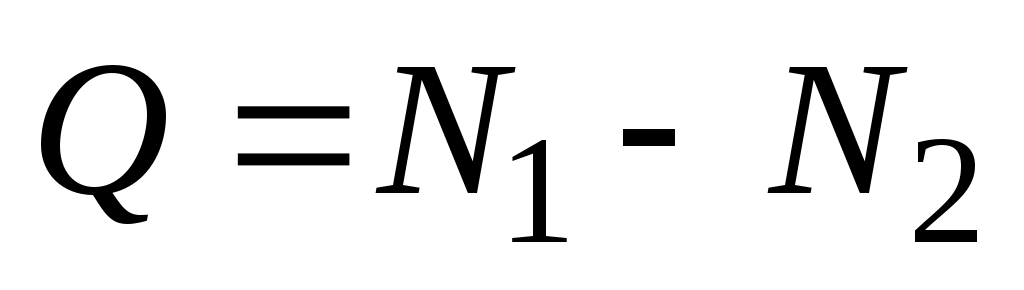 , (31)
, (31)
где N1 – разность отсчетов при измерениях с полюсом вне фигуры, N2 – разность отсчетов при измерениях с полюсом внутри фигуры.
1/2000, ошибка измерения угла должна быть не более 1 – 2''. Поэтому эти углы измерялись точными теодолитами Т1, Т2, либо на зрительную трубу устанавливали специальную насадку для точного измерения малых углов .
Описанный дальномер применим для измерения линий от 100 до 300 м. В настоящее время эти дальномеры вытеснены на производстве радио– и светодальномерами.
Радио– и светодальномеры
Принцип действия этих приборов основан на измерении времени t, за которое электромагнитные колебания проходят отрезок искомой линии. Такие дальномеры состоят из приемопередатчика, устанавливаемого на одном конце линии, и отражателя волн, располагаемого на другом ее конце. В процессе измерения луч света или радиоволна проходит двойное расстояние, и потому
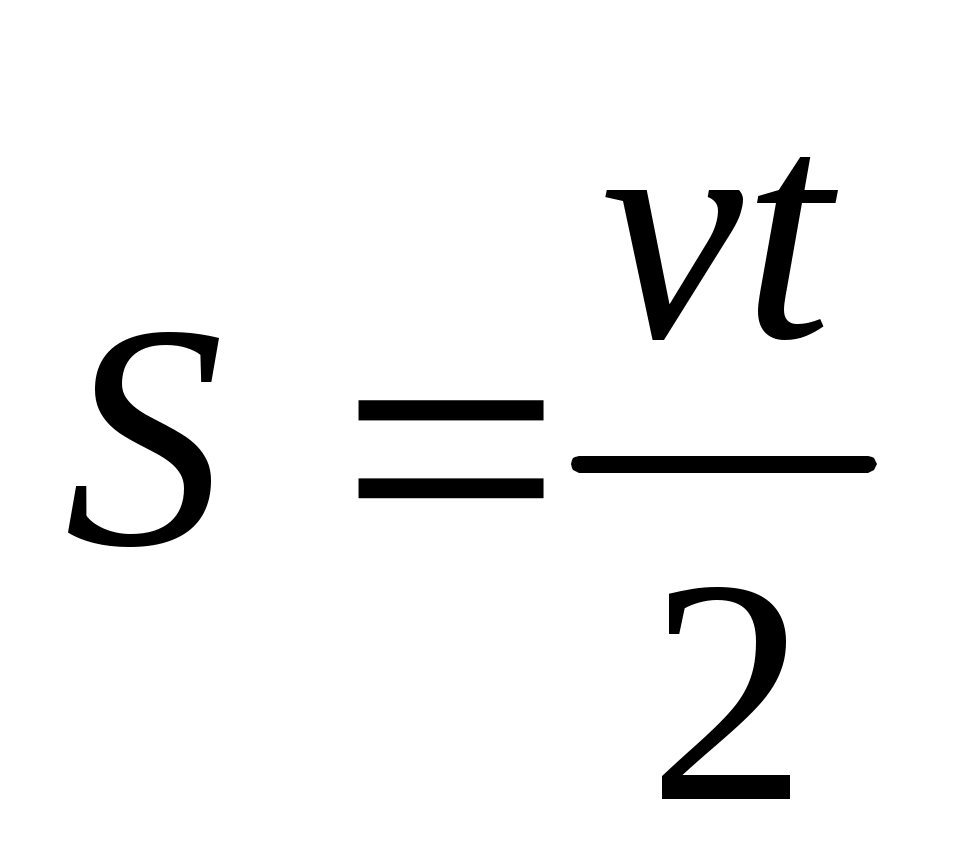 . (51)
. (51)
где v– скорость распространения электромагнитных колебаний в атмосфере. Так как скорость света в вакууме c = 299792,5 км/с 3108 м/с, то чтобы добиться точности измерений хотя бы до 1 м, время t прохождения сигнала должно регистрироваться с погрешностью t<0,710–8 сек.
Современные дальномеры бывают двух видов: импульсные, в которых время t измеряют прямым путем с помощью осциллографа (в военных локаторах), и фазовые дальномеры, в которых время t находят по разности фаз поданного и принятого сигналов.
Импульсные дальномеры нашли широкое применение в космических исследованиях, а фазовые дальномеры непрерывного действия – в наземных измерениях. В этих дальномерах мерой для измерения расстояний служит длина волны модулированных электромагнитных колебаний, и искомое расстояние
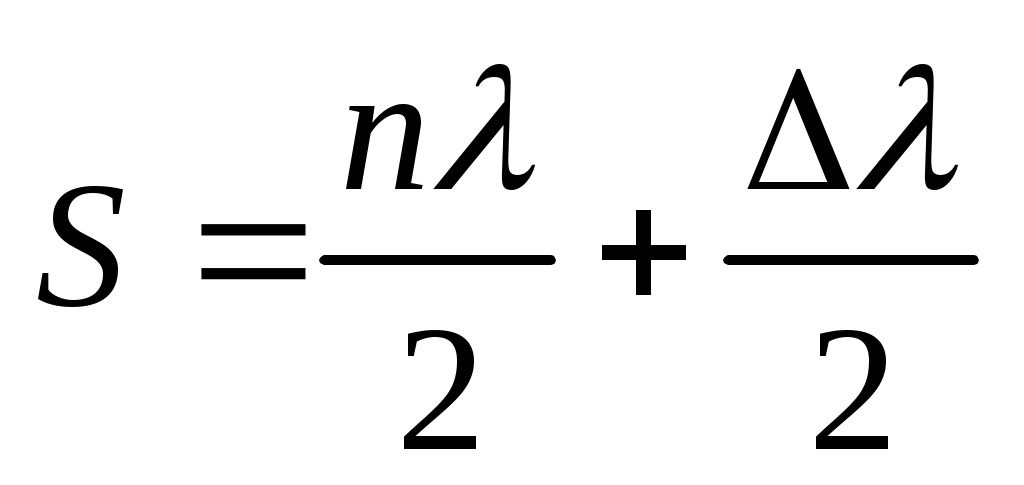 , (52)
, (52)
где n – число уложений волн в двойном измеренном отрезке, – домер, определяемый по фазовому углу . Для решения неоднозначности при определении числа n измерения выполняют на разных частотах с известными длинами волн. Современные дальномеры снабжены счетно–решающими устройствами и световыми табло, на котором показывается результат измерений.
В измеренное расстояние вносят три поправки: за метеоусловия наблюдений, наклон линии к горизонту и постоянное слагаемое. Точность таких дальномеров характеризуется погрешностью 0,2 – 2 см.
В последнее время в строительной практике нашли применение компактные лазерные рулетки, с помощью которых бесконтактным способом (без отражателей) с достаточной точностью измеряются небольшие расстояния и размеры строительных конструкций.
Лекция 5
Измерение превышений – нивелирование
Интервал сетки прямоугольных координат на картах масштаба 1:10000 1:100000 бывает равным 1 км или 2 км. Целое число километров абсцисс и ординат подписывается за внутренней рамкой карты у горизонтальных и вертикальных линий этой сетки.
Высота сечения рельефа подписывается под южной рамкой карты; там же может быть показан график заложений для определения крутизны скатов по расстояниям между горизонталями.
Величины магнитного склонения и сближения меридианов указаны у южной рамки карты. Там же дается схематичный чертеж взаимного расположения основных ориентирных линий – истинного и магнитного меридианов и оси абсцисс (см. рис.1.12).
Измерение площадей фигур
Существуют три способа измерения площадей на картах: графический, аналитический и механический.
П
Рис.1.29. Определение площади по
координатам вершин

ри графическом способеизмеряемый контур разбивается на ряд геометрических фигур, с помощью поперечного масштаба измеряются их элементы и вычисляются площади, которые затем суммируются. Второй вариант графического способа предусматривает использование палетки – сетки квадратов, нанесенной на лист прозрачной бумаги. Зная площадь каждого квадрата в масштабе карты, подсчитывают число полных квадратов, покрывающих заданный контур, а из неполных на глаз составляют полные. Затем все числа складывают.
Аналитический способпредназначен для определения площадей многоугольников по координатам их вершин.
На рис.1.29 искомую площадь многоугольника P1234 можно представить как функцию площадей прямоугольных трапеций: P1234=P1’122’+P2’233’-P4’433’-P1’144’.
Основания каждой трапеции здесь равны абсциссам X
точек, а высота – разностям ординат Y.
Поэтому
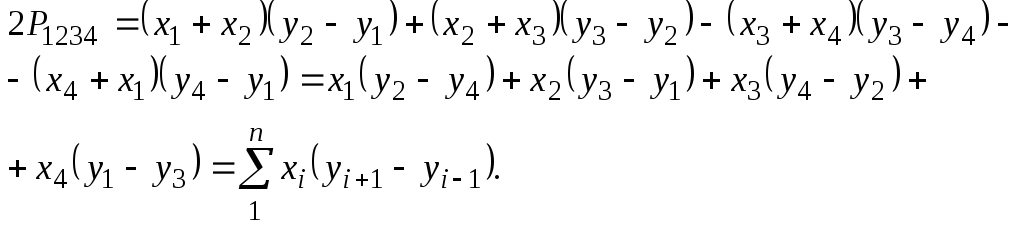 (27)
(27)М
Рис.1.30. Схема планиметра
 еханический способпредполагает использование специального прибора для измерения площадей – планиметра. Современный полярный планиметр состоит из двух рычагов – полюсного и обводного (рис.1.30, 1.31), которые соединяются шарнирно. На обводном рычаге расположен счетный механизм, а на конце рычага – обводной шпиль или прозрачная марка с точкой, которой обводится контур. Для измерения площади небольших фигур полюс устанавливают вне фигуры с таким расчетом, чтобы при обводе контура углы α между полюсным и обводным рычагами находились в пределах 30˚≤α≤150˚.
еханический способпредполагает использование специального прибора для измерения площадей – планиметра. Современный полярный планиметр состоит из двух рычагов – полюсного и обводного (рис.1.30, 1.31), которые соединяются шарнирно. На обводном рычаге расположен счетный механизм, а на конце рычага – обводной шпиль или прозрачная марка с точкой, которой обводится контур. Для измерения площади небольших фигур полюс устанавливают вне фигуры с таким расчетом, чтобы при обводе контура углы α между полюсным и обводным рычагами находились в пределах 30˚≤α≤150˚. Для измерения площади до начала обвода марка (обводной шпиль) устанавливается на контур фигуры и снимается начальный отсчет n1. Этот отсчет состоит из числа полных оборотов диска (снимается по циферблату), числа целых делений барабана, прошедших до нуля верньера (две цифры), и долей деления, снимаемых по совпадающему штриху нониуса (верньера).
Так, отсчет на рис.1.31 n=6458.
После обвода фигуры и возвращения в начальную точку снимается второй отсчет n2. Площадь фигуры в делениях планиметра P=(n2-n1) делений. Если известна цена одного деления планиметра μ (в квадратных метрах или гектарах), то искомая площадь составит
Для определения цены деления планиметра необходимо измерить этим прибором площадь какой-либо фигуры с известными размерами и площадью P0 (например, один или несколько квадратов координатной сетки). Тогда

Рис.1.31. Планиметр
В целях контроля и повышения точности площадь фигуры измеряют несколько раз.
Если измеряемый участок велик, то полюс планиметра ставят внутри фигуры. Тогда
Для определения постоянного числа Qнеобходимо и достаточно измерить площадь одного и того же участка с полюсом вне фигуры и внутри фигуры. Если при этом получена разность отчетов
где N1 – разность отсчетов при измерениях с полюсом вне фигуры, N2 – разность отсчетов при измерениях с полюсом внутри фигуры.
Лекция 3.
ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ И СЪЕМКИ
Решение любых геодезических задач связано с измерениями. Обычно таким измерениям подлежат длины линий (расстояния), горизонтальные и вертикальные углы, превышения между точками, а также вспомогательные величины: температура, атмосферное давление, время, частота излучения и др.
Измерить некоторую величину – значит сопоставить ее с другой, однородной величиной, принятой за единицу измерения. В нашей стране с 1918 года действует метрическая система мер, в которой в качестве основной единицы меры длины принят метр. По мысли создателей этой единицы (Франция, 1799 год) метр должен был равняться одной десятимиллионной части четверти земного меридиана. Эталон метра, изготовленный в 1889 году по результатам градусных измерений Парижского меридиана, был взят за основную международную единицу длины. Позднейшие, более точные измерения, показали, что четверть земного меридиана равна 10000856 м, а не 107 м, но введенную единицу длины было решено не менять. С 1983 года утверждено новое определение метра. Установлено, что метр равен расстоянию, которое проходит луч света в вакууме за 1/299792248 доли секунды.
Производными единицами от метра являются километр, дециметр, сантиметр, миллиметр, микрометр (10–6 м).
В качестве угловых мер в геодезии используются три меры:
а) градусная – окружность делится на 360˚, 1˚ – на 60΄, 1΄ – на 60˝;
б) градовая (центимальная). Окружность делится на 400 град (400g), 1g – на 100 центимальных минут (100c) и 1c – на 100 центимальных секунд (100cc).
Для перехода от градусной меры к градовой используют зависимость
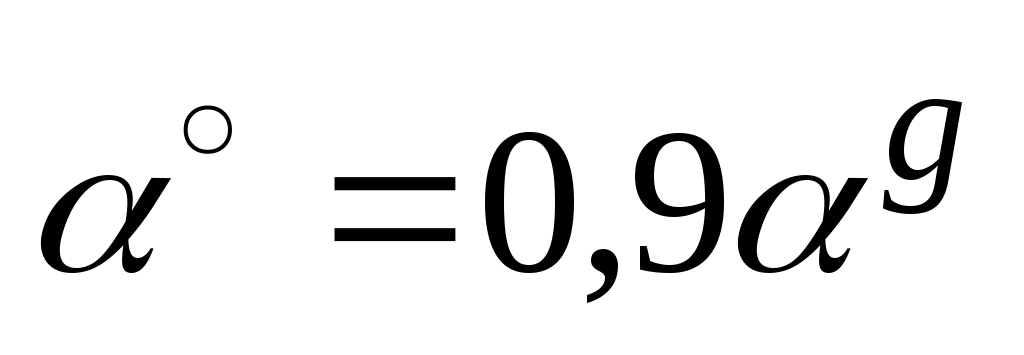 ; для обратного перехода
; для обратного перехода 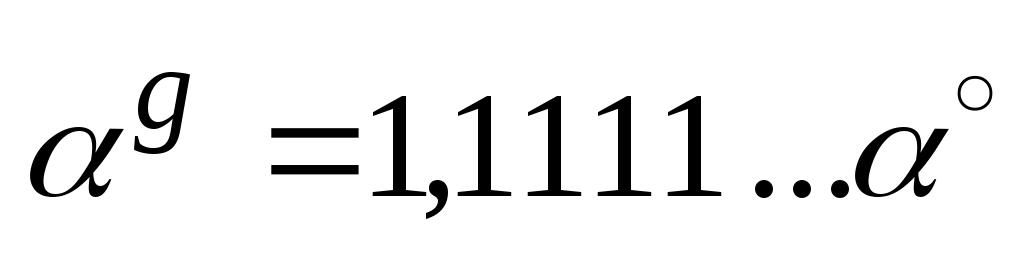 .
.
в) радианная (рис.2.1).
Р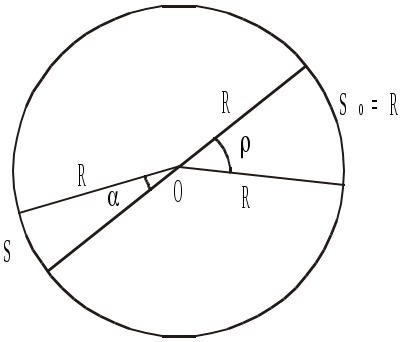 адиан (рад) – угол ρ между двумя радиусами круга, вырезающими на окружности дугу, равную радиусу (
адиан (рад) – угол ρ между двумя радиусами круга, вырезающими на окружности дугу, равную радиусу (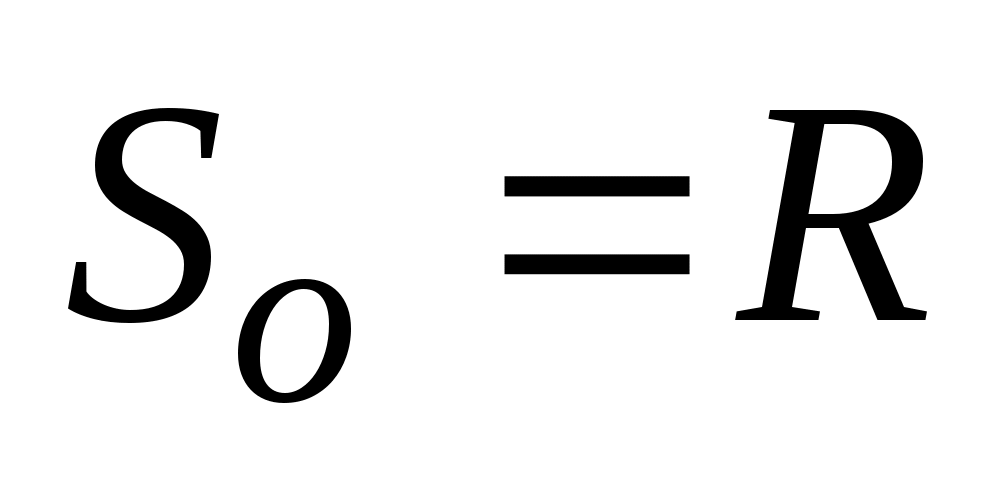 ). Из пропорции
). Из пропорции 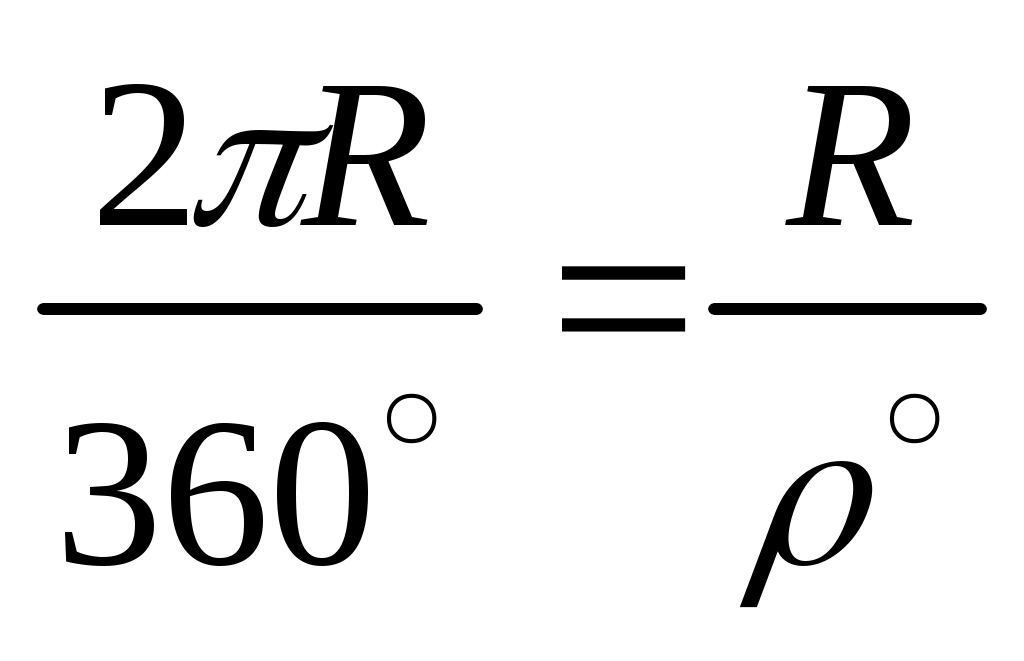 следует, что
следует, что
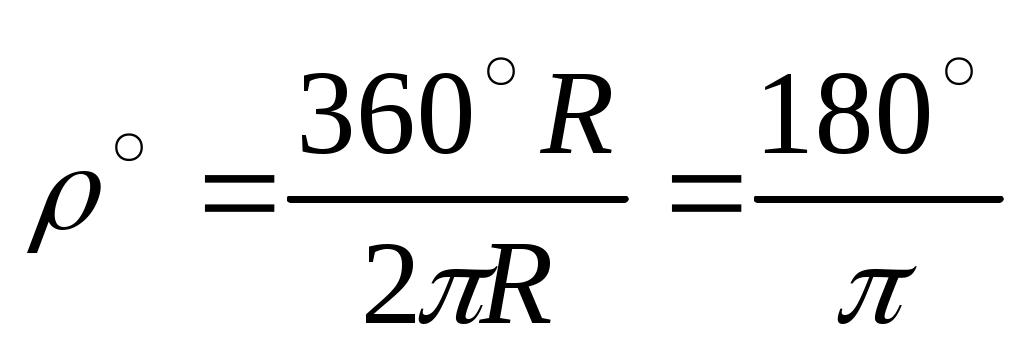 . (32)
. (32)
Рис.2.1. Радианная мера
Отсюда ρ˚=57,3˚; ρ΄=3438΄; ρ˝=206265˝.
При известной дуге S окружности угол α, выраженный в радианах, 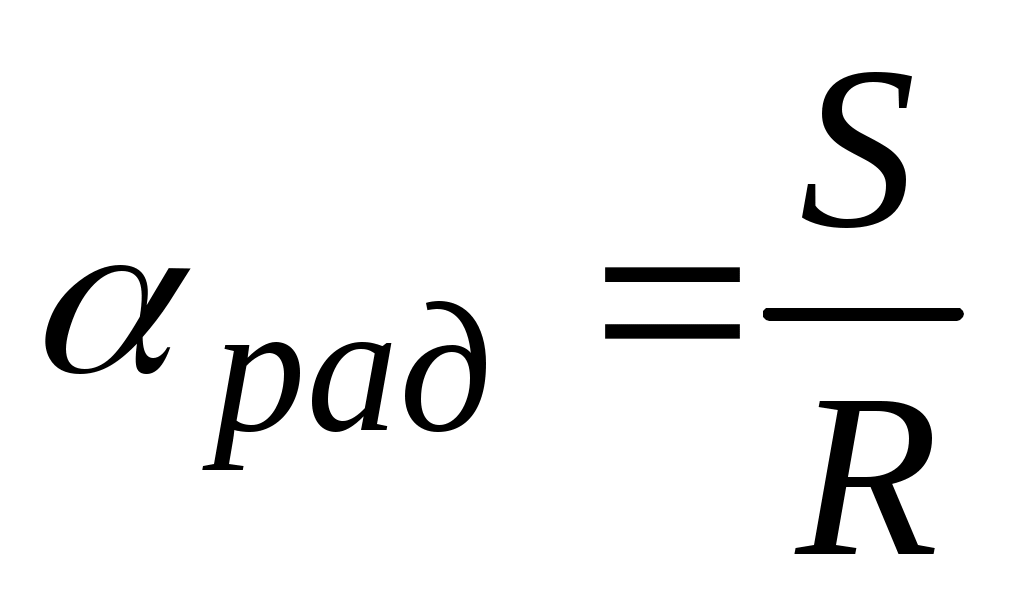 .
.
Переход от градусной меры к радианной осуществляется по формуле
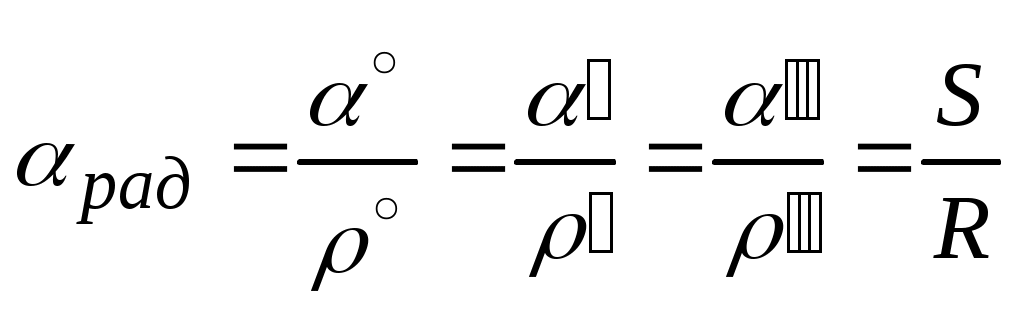 . (33)
. (33)
Радианную меру широко применяют при приближенных вычислениях, учитывая, что для малых углов (до 2˚ – 3˚) справедливы соотношения
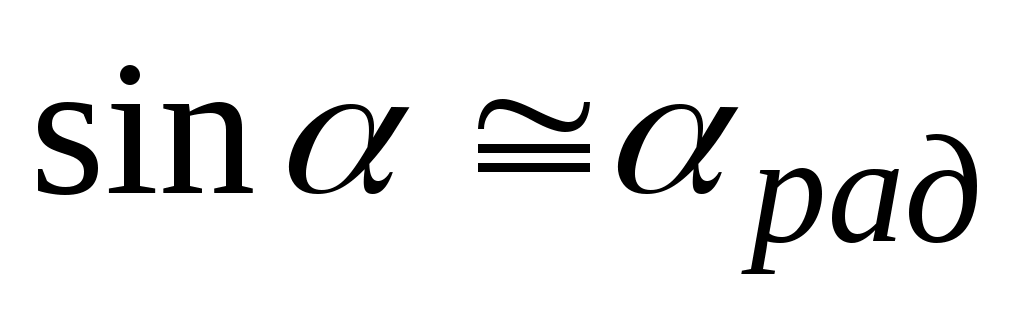 ;
; 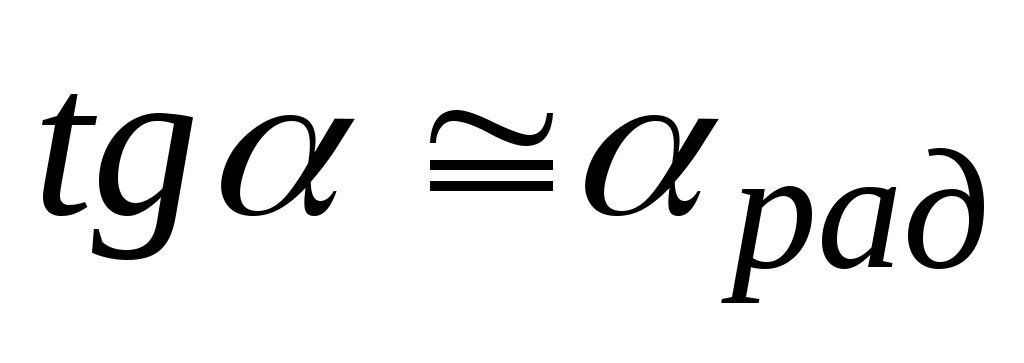 . (34)
. (34)
Меры площади в метрической системе: квадратный метр – м2; гектар = га = 100 м × 100 м = 10000 м2; ар = 100 м2 (сотка); квадратный километр = км2 = 100 га.
Угловые измерения
Для измерения горизонтальных и вертикальных углов в качестве основного прибора в геодезии используется теодолит.
а
б
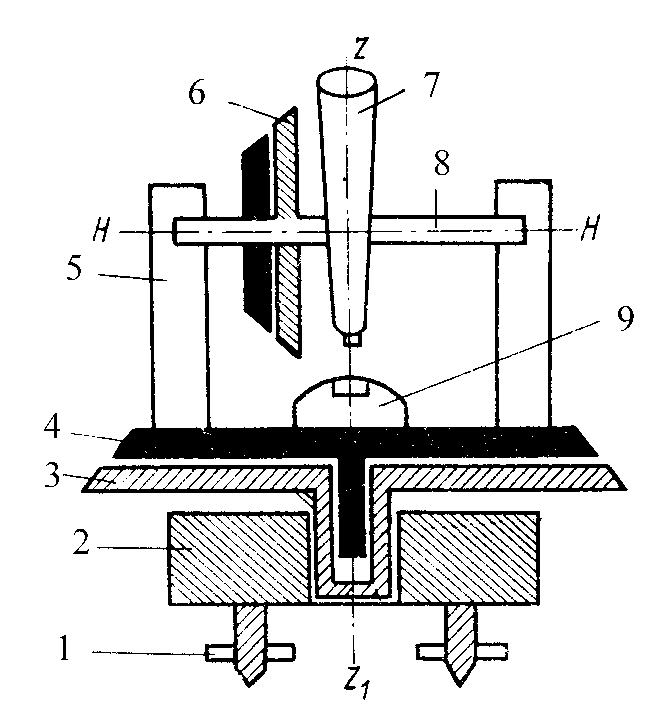
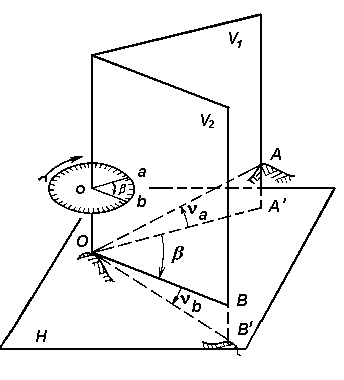
Рис.2.2. Теодолит
Горизонтальный угол β – это проекция пространственного угла ABC на горизонтальную плоскость.
На рис.2.2,а показана принципиальная схема такого проектирования, которая лежит в основе устройства теодолита. На рис.2.2,б показан его схематический вертикальный разрез: 3 – лимб горизонтального круга – металлическое или стеклянное кольцо с нанесенными на него градусными или минутными делениями; 4 – алидада горизонтального круга – концентрически связанное с лимбом кольцо, несущее на себе отсчетные приспособления, цилиндрический уровень 9 и подставки 5 зрительной трубы 7. Лимб и алидада своими осевыми втулками входят в подставку теодолита 2 с тремя подъемными винтами 1. На рис.2.2,б показана также ось вращения 8 зрительной трубы и вертикальный круг 6, также состоящий из лимба и алидады. Основные части теодолита снабжены закрепительными и наводящими винтами.
В теодолите элементы проекции (см. рис.2.2,а) реализуются так: горизонтальной плоскостью проекции H служит плоскость лимба горизонтального круга; вместо двух отвесных проектирующих плоскостей v1иv2теодолит имеет одну подвижную проектирующую коллимационную плоскость, которую должна описывать визирная ось зрительной трубы при вращении вокруг горизонтальной оси 7 (см. рис.2.2). Вершина О угла на плоскости H представлена центром лимба горизонтального круга.
Зрительная труба теодолита предназначена для наблюдения удаленных предметов и построена по телескопической системе (рис.2.3), в которой при установке трубы на бесконечность точка заднего фокуса объектива совмещается с точкой переднего фокуса окуляра.
Рис.2.3. Зрительная труба
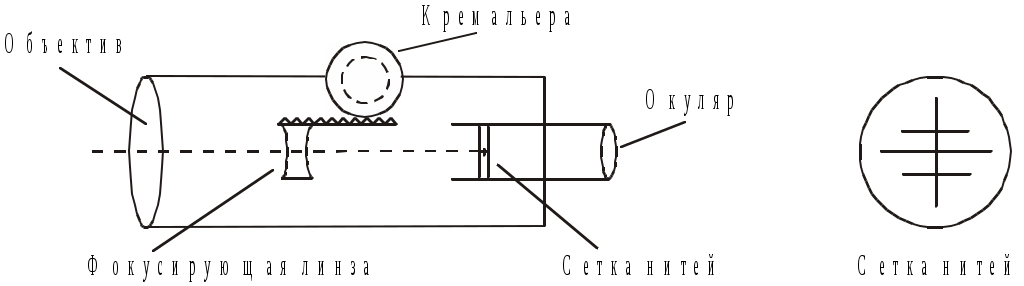
Визирной осью зрительной трубы называют воображаемую линию, соединяющую оптический центр объектива и точку пересечения нитей сетки.
При геодезических работах расстояния до наблюдаемых точек конечны, поэтому изображения предметов в трубе могут занимать разные позиции, в зависимости от расстояний до наблюдаемых точек. Поэтому для наблюдений зрительную трубу устанавливают по глазу и по предмету. В первом случае ее направляют на светлый фон и, вращая диоптрийное кольцо окулярного патрубка, достигают четкой видимости нитей сетки. Для установки трубы по предмету нужно добиться четкого изображения предмета. Оно будет таким только тогда, когда изображение предмета в трубе совместится с плоскостью сетки нитей. Это достигается перемещением фокусирующей линзы с помощью кремальеры.
Уровни предназначены для установки осей или плоскостей геодезических приборов в горизонтальное или отвесное положение, либо для измерения небольших углов наклона. Различают два вида уровней: более точные – цилиндрические и менее точные – сферические, круглые уровни.
Цилиндрический уровень представляет собой стеклянную ампулу тороидальной формы, запаянную в металлическую оправу. В продольном сечении внутренняя поверхность ампулы отшлифована по дуге окружности радиуса R (рис.2.4). Ампула заполнена спиртом или эфиром. Свободное пространство в ней, заполненное парами жидкости, называется пузырьком уровня, который всегда стремится занять самое высокое положение в ампуле. На внешней поверхности ампулы нанесена шкала делений (обычно через 2 мм).
Осью уровня (рис.2.4) называется касательная к внутренней поверхности ампулы в нуль–пункте, а ценой деления – центральный угол τ, опирающийся на одно деление уровня.
Если пузырек уровня находится в нуль–пункте, то ось уровня занимает в пространстве горизонтальное положение. Наклон ν оси уровня относительно горизонта определяют по величине смещения пузырька относительно нуль–пункта (ν=n∙τ). В технических теодолитах τ бывает в пределах 30˝ – 60˝, в нивелирах 5˝ – 30˝.
Круглые уровни предназначены для предварительной установки прибора в рабочее положение. Внутренняя поверхность ампулы такого уровня отшлифована под сферу некоторого радиуса. На внешней поверхности нанесены концентрические деления. Осью круглого уровня является радиус сферы, опущенный из нуль–пункта. Цена деления круглого уровня обычно равна 5΄ – 10΄.
Горизонтальный круг теодолита состоит из двух частей – лимба и алидады. По внешнему краю лимба нанесены градусные и минутные деления. Счет делений идет по ходу часовой стрелки. Наименьшее деление лимба есть цена его деления.
Алидада – концентрически связанный с лимбом круг, на котором расположены отсчетные приспособления. На кожухе алидады крепятся подставки зрительной трубы. В процессе измерения горизонтального круга лимб теодолита остается неподвижным, а трубу вместе с алидадой устанавливают в заданном направлении по сторонам угла.
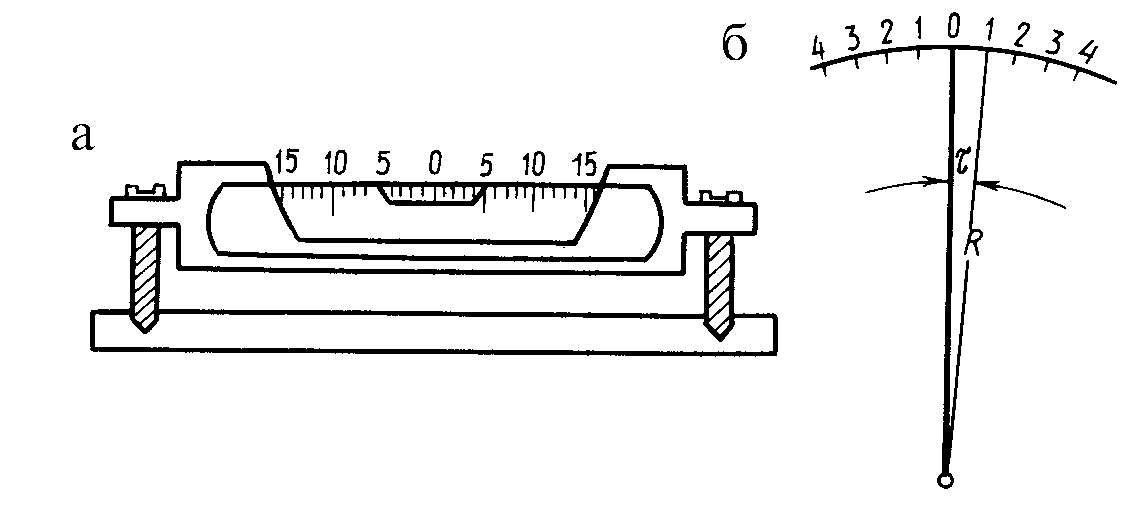
Рис.2.4. Цилиндрический уровень: а – устройство уровня;
б – цена деления уровня
Отсчетные приспособления
Отсчетом называют угол, отсчитанный по ходу часовой стрелки от нулевого деления лимба до указателя (нулевого штриха) отсчетного приспособления.
В современных технических теодолитах со стеклянными кругами отсчетными приспособлениями служат штриховой (рис.2.5) или шкаловой (рис.2.6) микроскопы. В первом случае отсчет по лимбу берут на глаз по штриху указателя.
Н
Рис.2.5. Штриховой микроскоп лимба
Рис.2.6. Шкаловой микроскоп
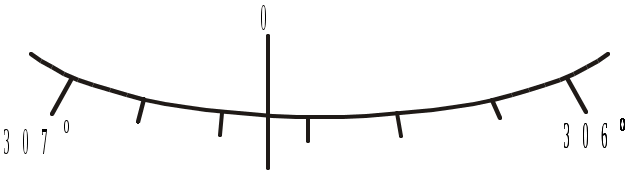
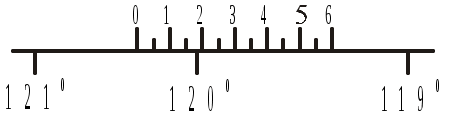
а рис.2.5 отсчет A= 306˚ 35΄ при цене деления лимба 10΄. В поле зрения шкалового микроскопа видны деления лимба и шкала, размер которой равен одному делению. Отсчет здесь состоит из целого числа делений лимба, к которому прибавляют отсчет по шкале.
На рис.2.6 A= 120˚ + 18΄ = 120˚ 18΄, так как наименьшее деление микроскопа 5΄, а цифры от 0 до 6 шкалы означают десятки минут.
Поверки теодолита
В соответствии с принципиальной схемой теодолита (рис.2.2) между его осями и плоскостями должны соблюдаться определенные геометрические соотношения, которые нужно проверить и при необходимости исправить.
1–е условие. Ось цилиндрического уровня на алидаде горизонтального круга должна быть перпендикулярна оси вращения инструмента. Соблюдение этого условия должно обеспечить возможность установки с помощью уровня горизонтального круга в горизонтальное положение.
П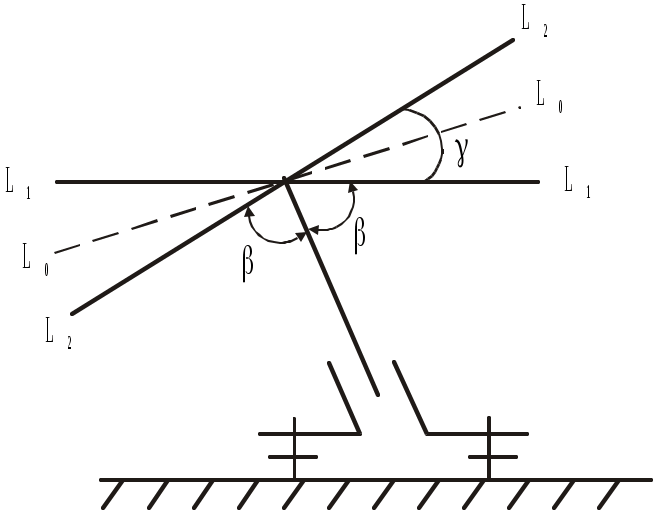 орядок поверки следующий. Предварительно пузырек уровня на алидаде ставят примерно в нуль–пункт тремя подъемными винтами. Затем ампулу уровня располагают так, чтобы она стала параллельно линии, соединяющей два подъемных винта, и, действуя этими винтами, приводят пузырек уровня в нуль–пункт, а ось уровня L1–L1 – в горизонтальное положение (рис.2.7). При этом ось может оказаться не перпендикулярна оси вращения прибора (β ≠ 90˚).
орядок поверки следующий. Предварительно пузырек уровня на алидаде ставят примерно в нуль–пункт тремя подъемными винтами. Затем ампулу уровня располагают так, чтобы она стала параллельно линии, соединяющей два подъемных винта, и, действуя этими винтами, приводят пузырек уровня в нуль–пункт, а ось уровня L1–L1 – в горизонтальное положение (рис.2.7). При этом ось может оказаться не перпендикулярна оси вращения прибора (β ≠ 90˚).
А
Рис.2.7. Поверка уровня
лидаду поворачивают на 180˚ и, если пузырек уровня отклонится от нуль–пункта, то это свидетельствует о том, что ось уровняL2–L2 наклонилась к горизонту на угол γ, равный дуге смещения пузырька уровня.
Согласно рис.2.7: 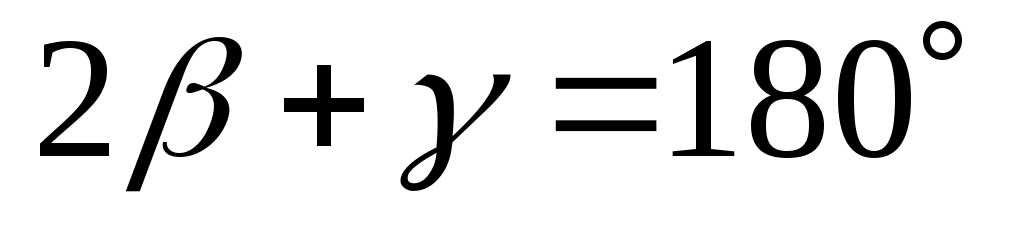 и
и 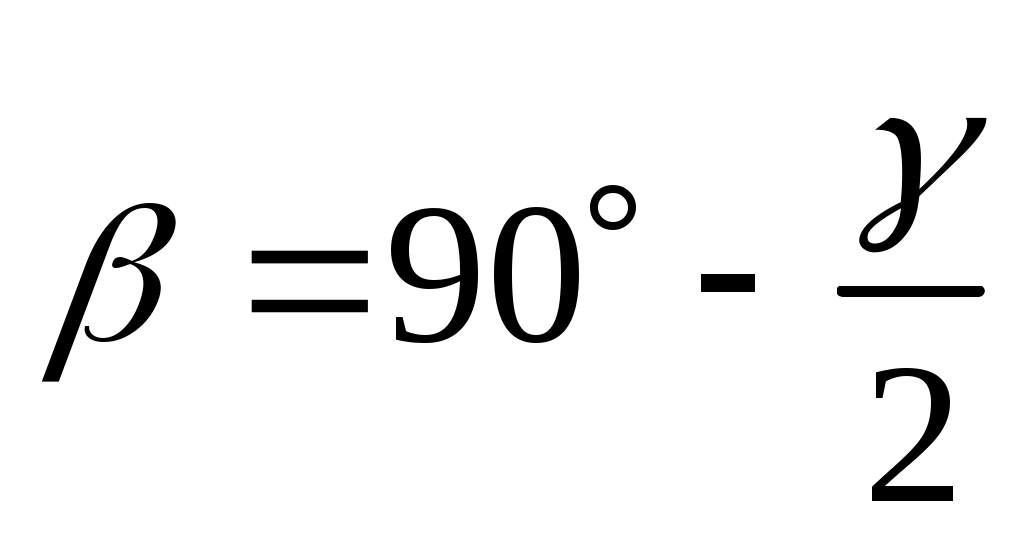 . Поэтому, если β90˚, то необходимо исправительными винтами уровня переместить пузырек в сторону середины на половину дуги отклонения, поставив ось в положение L0–L0. Наконец, подъемными винтами пузырек приводят в нуль–пункт и для контроля поверку повторяют.
. Поэтому, если β90˚, то необходимо исправительными винтами уровня переместить пузырек в сторону середины на половину дуги отклонения, поставив ось в положение L0–L0. Наконец, подъемными винтами пузырек приводят в нуль–пункт и для контроля поверку повторяют.
2–е условие. Визирная ось зрительной трубы должна быть перпендикулярна ее оси вращения. Условие ставится для того, чтобы визирная ось при вращении описывала проектирующую коллимационную плоскость, а не коническую поверхность. Угол c, на который отклоняется визирная ось от перпендикуляра и оси вращения трубы, называется коллимационной ошибкой. Поверку выполняют путем двукратного визирования на удаленную точку местности A, расположенную примерно на уровне прибора, со взятием отсчетов по горизонтальному кругу. Первое наведение осуществляют при положении трубы «круг лево» (КЛ), второе (после поворота через зенит) – при положении трубы «круг право» (КП).
На рис.2.8 B–B – ось вращения трубы; A1–Aи A2–A – положение визирной оси при КП и КЛ. Коллимационная ошибка
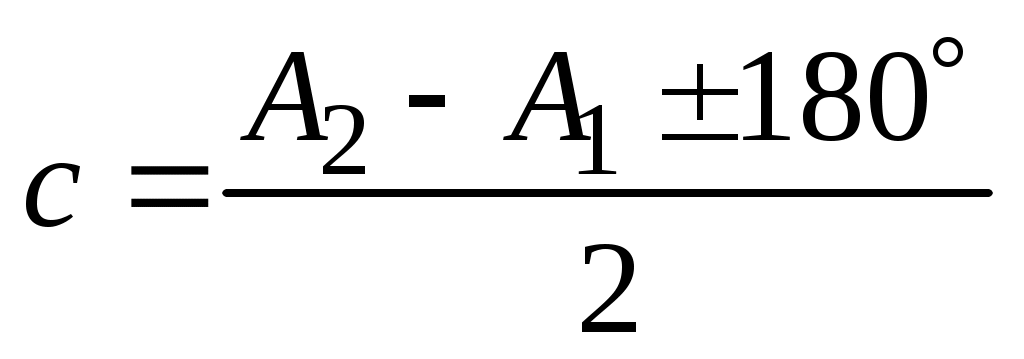
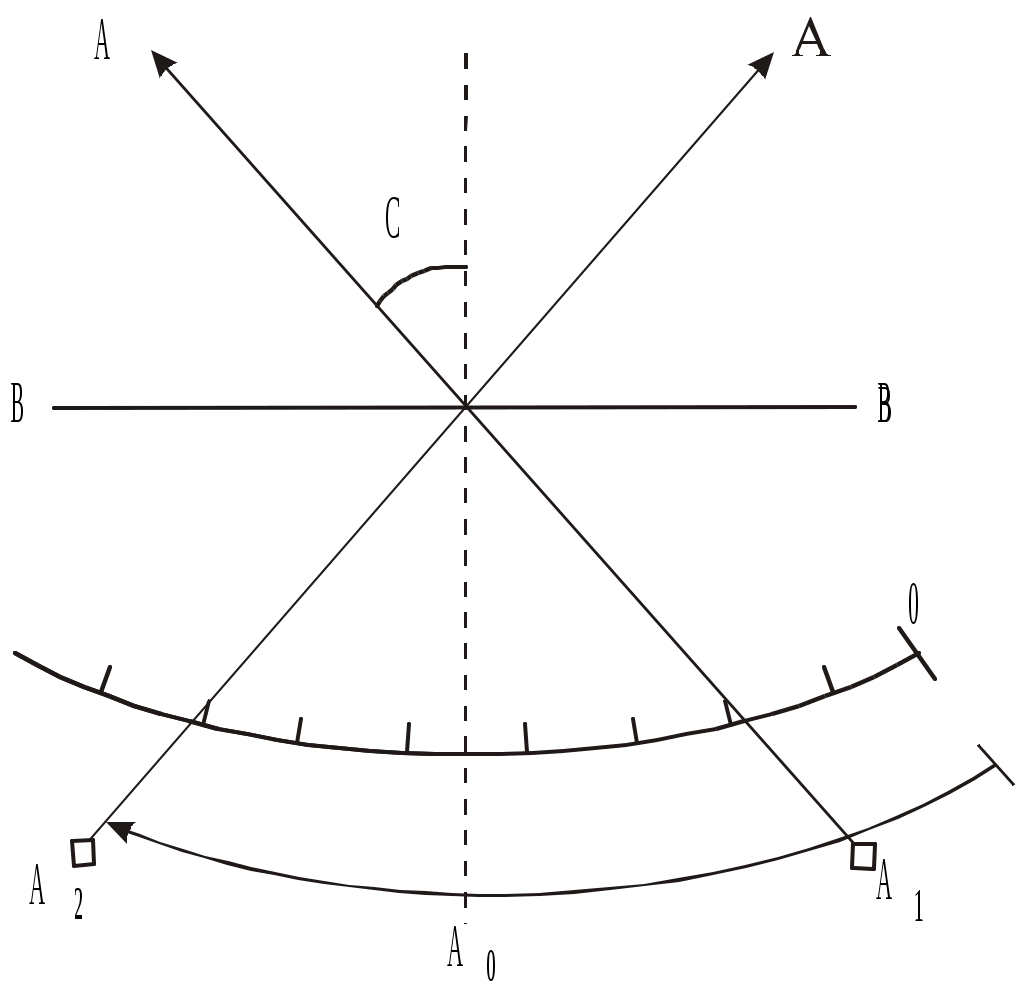 . (35)
. (35)
Если окажется, что c > 2΄ (больше двойной точности отсчета), эту ошибку нужно исправить. Для этого алидаду устанавливают на отсчет A0, свободный от влияния коллимационной ошибки:
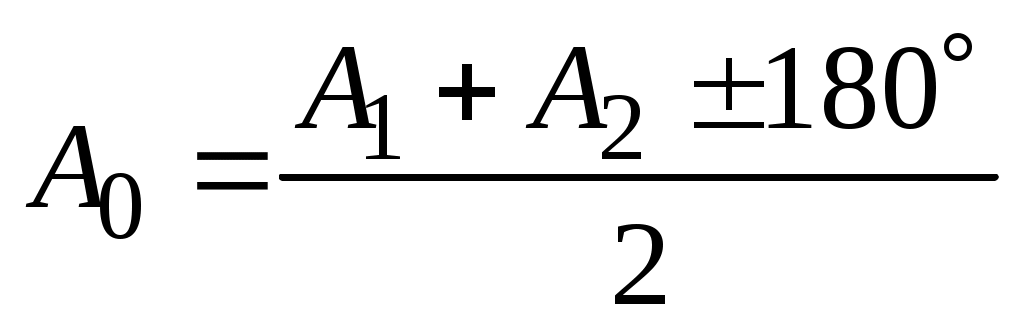 . (36)
. (36)
Рис.2.8. Коллимационная ошибка
Глядя в зрительную трубу, можно увидеть, что крест нити сошел с наблюдаемой точки A. Для устранения ошибки сетку нитей передвигают горизонтальными исправительными винтами до совмещения с наблюдаемой точкой. Для контроля поверку повторяют.
Пример: отсчет A1(КП) = 25° 30΄;
отсчет A2(КЛ) = 205° 34΄;
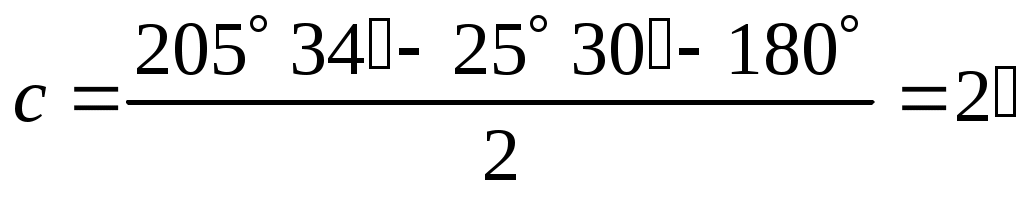 ;
;
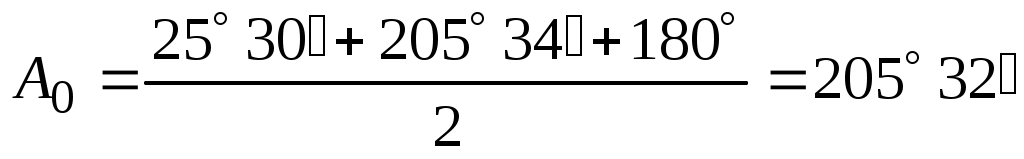 .
.
3–е условие. Ось вращения зрительной трубы должна быть перпендикулярна оси вращения теодолита. В современных приборах соблюдение этого условия гарантировано заводом–изготовителем.
Измерение горизонтальных углов
Принцип измерения горизонтальных углов показан на рис.2.9. Теодолит устанавливают по отвесу над вершиной B угла с точностью 3 – 5 мм (для измерений технической точности) и приводят в рабочее положение по уровню. Над наблюдаемыми точками или позади них располагают визирные цели (вешки).
Порядок измерения горизонтального угла способом приемов рекомендуется следующий:
1) при закрепленном лимбе зрительную трубу наводят на левую точку A1 и снимают отсчет по горизонтальному кругу a1;
2) зрительную трубу наводят на правую точку A2 и снимают отсчет a2;
3) угол β находят как разность отсчетов 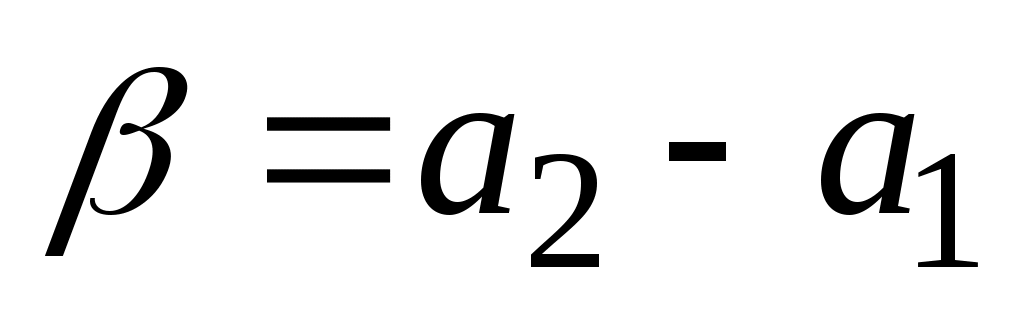 (если a2<a1, то к отсчету a2 прибавляют 360°).
(если a2<a1, то к отсчету a2 прибавляют 360°).
Э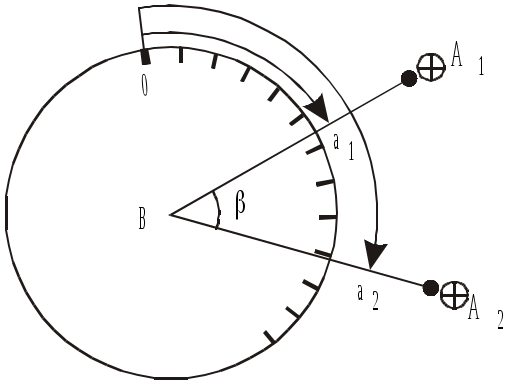 ти операции составляют один полуприем. Для исключения остаточного влияния инструментальных погрешностей и повышения точности измерений все операции повторяют при другом положении зрительной трубы (после поворота ее через зенит), то есть выполняют второй полуприем (желательно при другой установке лимба).
ти операции составляют один полуприем. Для исключения остаточного влияния инструментальных погрешностей и повышения точности измерений все операции повторяют при другом положении зрительной трубы (после поворота ее через зенит), то есть выполняют второй полуприем (желательно при другой установке лимба).
Е
Рис.2.9. Измерение
горизонтального угла
сли значения углов β1 и β2 в двух полуприемах различаются не более чем на 1΄, то вычисляют среднее значение угла. В противном случае измерения повторяют при другой установке лимба.
Измерение вертикальных углов
Вертикальным углом называют угол наклона визирной оси зрительной трубы относительно горизонта. Он может быть в пределах от 0˚ до 90˚ и иметь знак “+”, если труба направлена выше горизонта, и знак “–” если труба направлена ниже горизонта.
Для измерения вертикальных углов теодолит снабжен вертикальным кругом, состоящим из лимба и алидады. В отличие от горизонтального круга здесь лимб жестко связан с трубой, а алидада ставится в рабочее положение по уровню или автоматически с помощью маятникового компенсатора.
Измеряемый угол наклона равен разности двух отсчетов: отсчета при наклонном положении трубы и заранее вычисленного отсчета, соответствующего горизонтальному положению трубы. Этот отсчет называют местом нуля (М0) вертикального круга.
Для разных конструкций вертикальных кругов формулы для вычисления М0 и углов наклона ν различны. Они зависят от вида оцифровки делений вертикального круга. Например, для наиболее распространенных теодолитов 2Т30 с плюсовой и минусовой оцифровкой делений эти формулы такие:
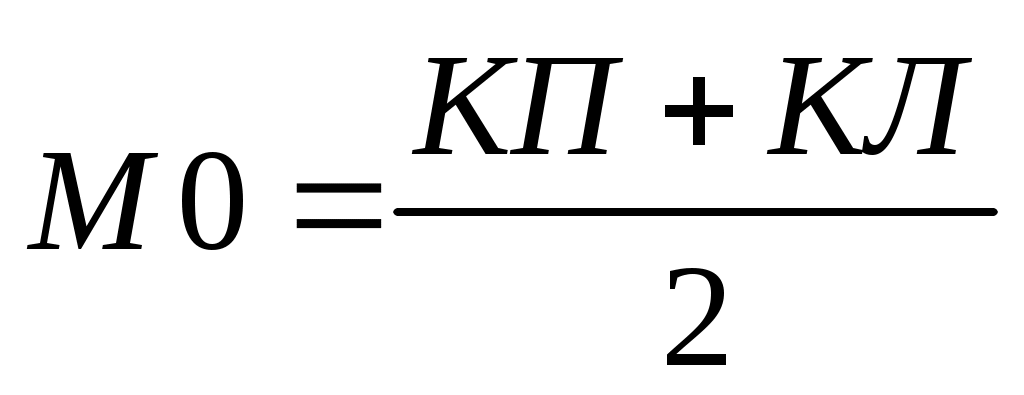 ;
; 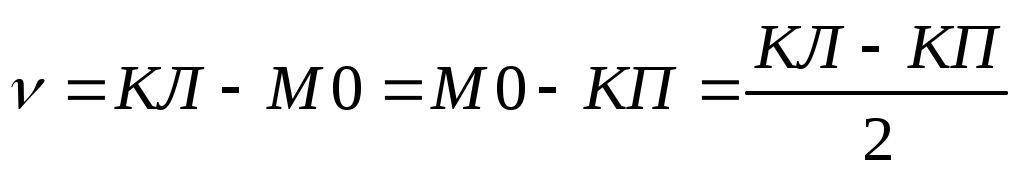 , (37)
, (37)
где КП и КЛ – отсчеты по вертикальному кругу при наведении на некоторую точку при двух положениях трубы.
Например, КЛ = + 5˚ 10΄; КП = – 5˚ 20΄; М0 = – 0˚ 05΄;
ν = 5˚ 10΄ – ( – 0˚ 05΄) = + 5˚ 15΄ = – 0˚ 05΄ – ( – 5˚ 20΄) = + 5˚ 15΄.
Для теодолитов Т2, Т5 с круговой оцифровкой делений круга формулы имеют вид
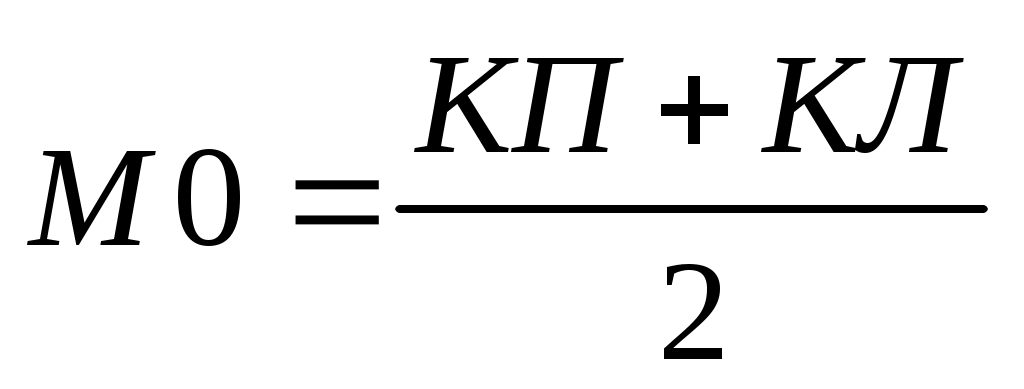 ;
; 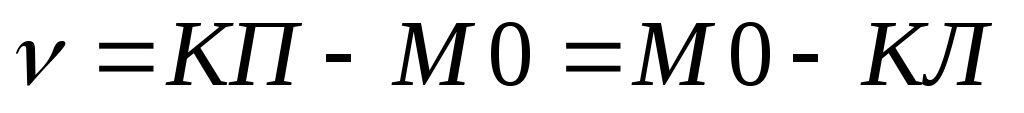 . (38)
. (38)
При вычислении углов по последним формулам ко всем отсчетам, меньшим 90˚, прибавляют 360˚, имея ввиду, что М0 здесь не может быть отрицательным числом, а углы наклона могут изменяться в пределах от 0˚ до 90˚. Например, КП = 356˚ 41΄, КЛ = 3˚ 15΄,
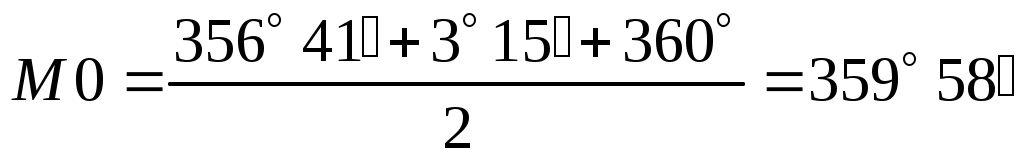 ,
, 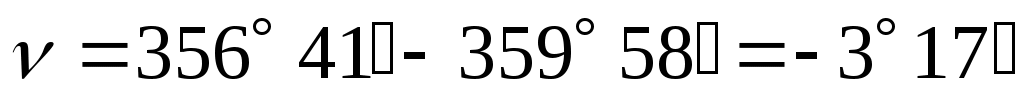 ;
;
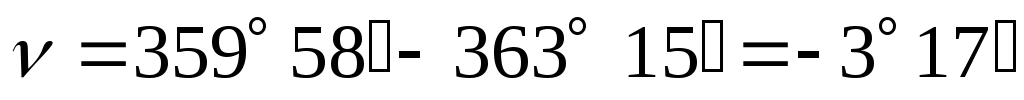 .
.
Лекция 4.
Линейные измерения
В настоящее время геодезия располагает большим арсеналом средств для линейных измерений. Мерные ленты и рулетки применяют для измерения небольших расстояний (до нескольких сот метров) с относительной ошибкой 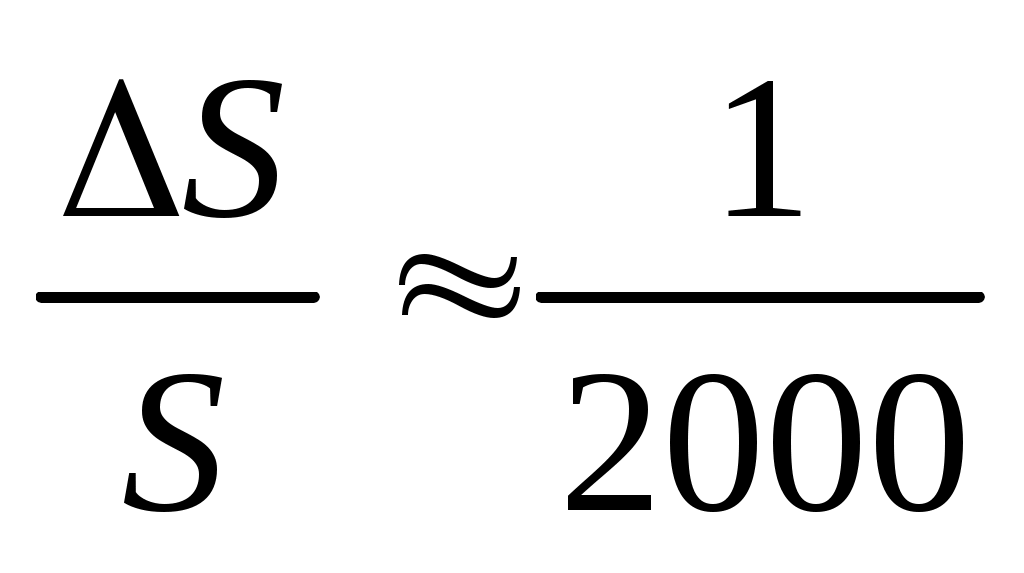 ; оптические дальномеры – для измерения линий от нескольких метров до 150 – 200 м с погрешностью
; оптические дальномеры – для измерения линий от нескольких метров до 150 – 200 м с погрешностью 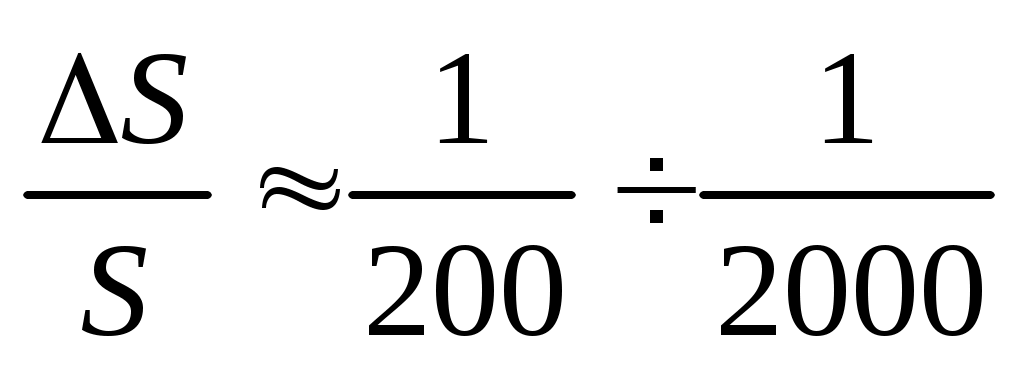 ; радио– и светодальномеры – для измерения расстояний в земных условиях до нескольких десятков километров с ошибкой 1 – 5 см. большие лазерные дальномеры используют в космических исследованиях.
; радио– и светодальномеры – для измерения расстояний в земных условиях до нескольких десятков километров с ошибкой 1 – 5 см. большие лазерные дальномеры используют в космических исследованиях.
Все линейные мерные приборы делятся на три категории: эталоны, образцовые и рабочие меры. Для установления фактической длины мерного прибора рабочую меру сравнивают с образцовой, а образцовую – с эталонной. Этот процесс называется компарированием. В ходе его определяют уравнение мерного прибора
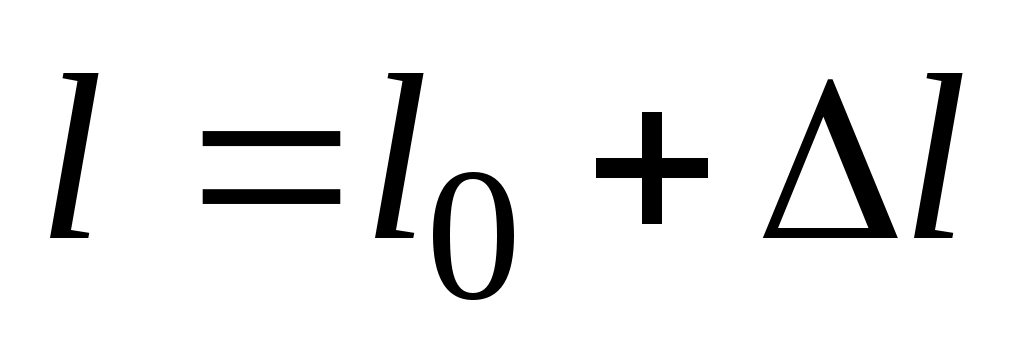 при
при 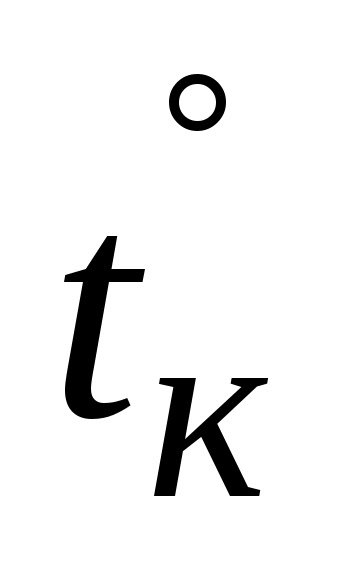 , (39)
, (39)
где l0 – номинальная длина рулетки (ленты), 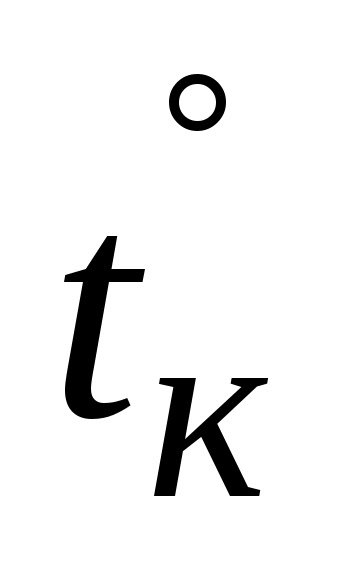 – температура компарирования.
– температура компарирования.
Иногда вместо сравнения с образцовой мерой рабочей рулеткой измеряют некоторый закрепленный отрезок на местности, ранее измеренный более точным прибором. Такой эталонный отрезок называют полевым компаратором. Если L0– длина полевого компаратора, L – результат измерения рабочей мерой, то поправка в ее длину
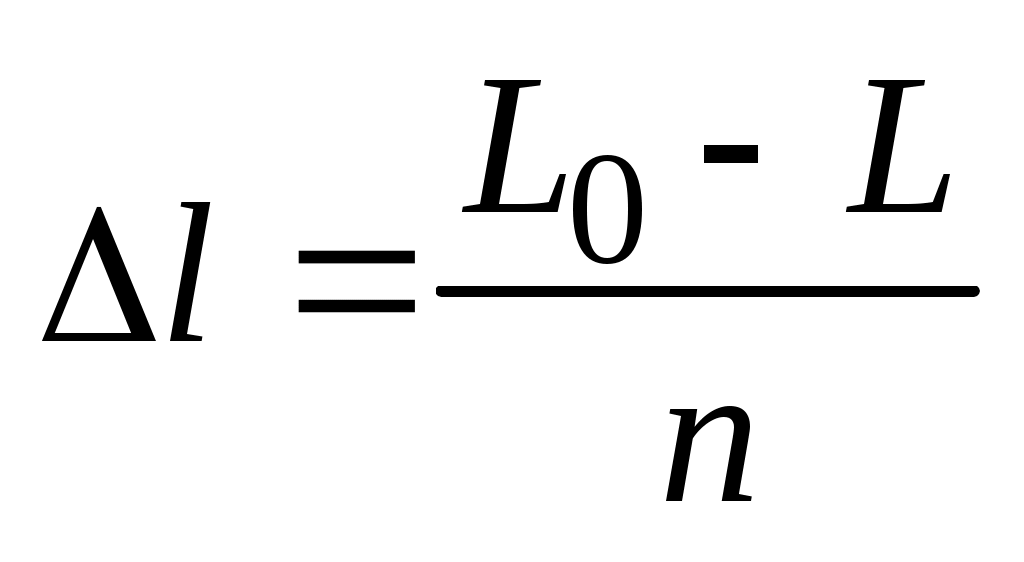 , (40)
, (40)
где n – число уложений рабочей меры в полевом компараторе. Например, L0= 100,00 м, l0= 20 м, L = 100,05 м, 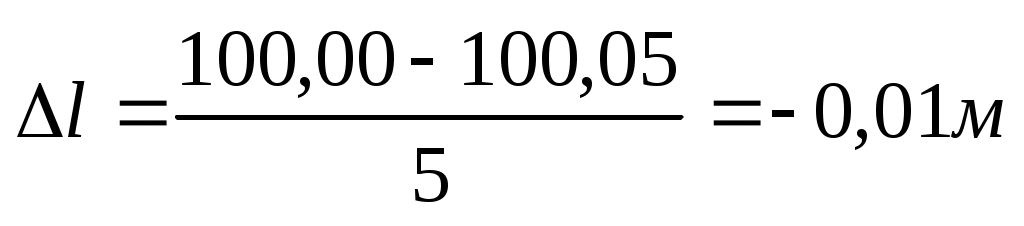 и
и 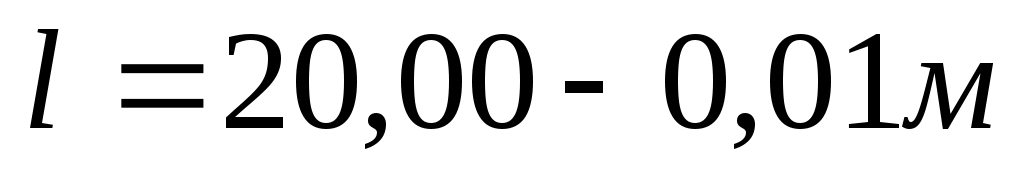 при
при 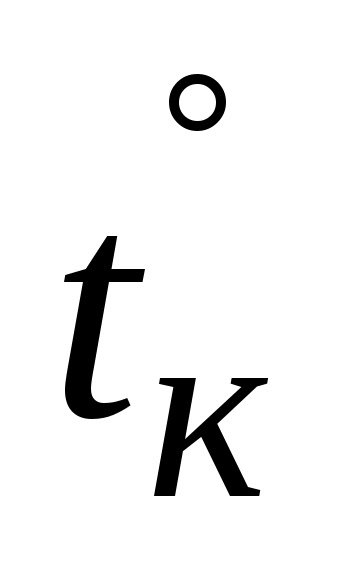 .
.
Измерение длин линий по земле мерными рулетками и лентами начинается после расчистки трассы. Если линия проходит по местности с несколькими перегибами, то ее разбивают на части, и каждый отрезок измеряют отдельно путем последовательного уложения рулетки по направлению измеряемой линии. Каждое уложение ленты фиксируется на земле металлической шпилькой.
Длину отрезка S находят по формуле
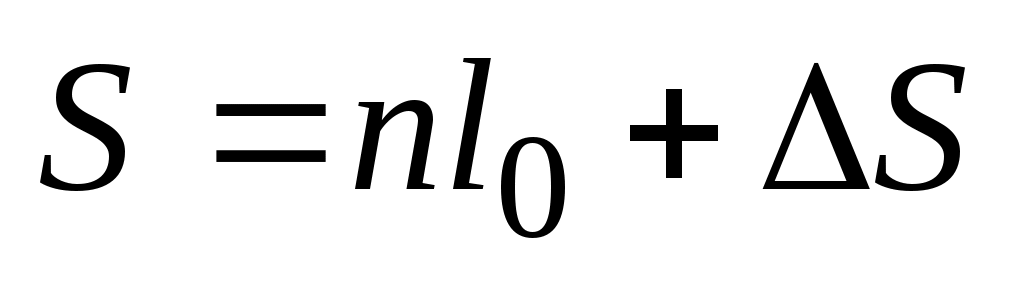 при
при  , (41)
, (41)
где 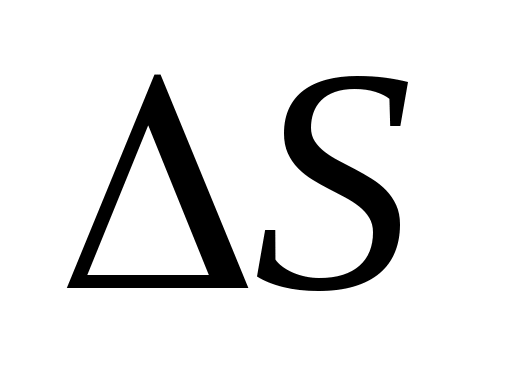 – домер (остаток). Для контроля каждый отрезок измеряют дважды в прямом и обратном направлении. Расхождения в результатах допустимы не более чем 5 см на каждые 100 м.
– домер (остаток). Для контроля каждый отрезок измеряют дважды в прямом и обратном направлении. Расхождения в результатах допустимы не более чем 5 см на каждые 100 м.
В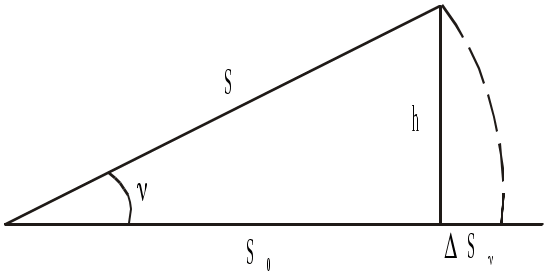 измеренную длину линии вводят три поправки:
измеренную длину линии вводят три поправки:
а) за длину мерного прибора (компарирование) 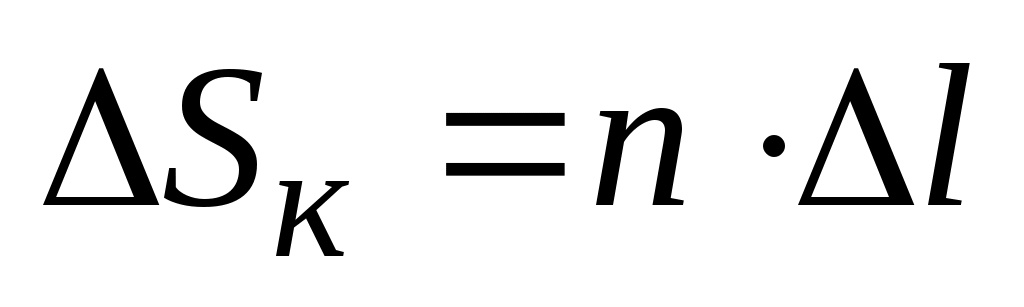 (знак поправки тот же, что у
(знак поправки тот же, что у  ),
),
Рис.2.10. Поправка
за наклон линии
б) за температуру измерений 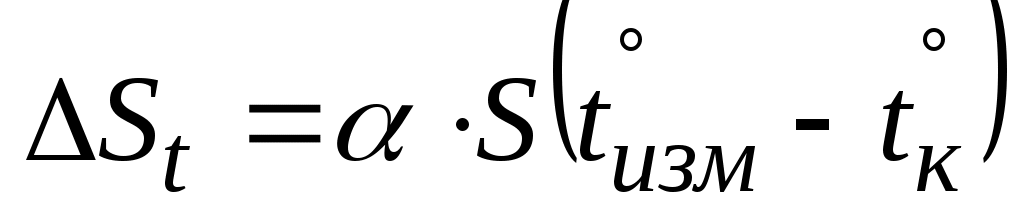 ,
,
где  – коэффициент линейного расширения материала, из которого изготовлена рулетка,
– коэффициент линейного расширения материала, из которого изготовлена рулетка,
в) за наклон линии к горизонту (рис.2.10) – при вычислении горизонтальной проекции 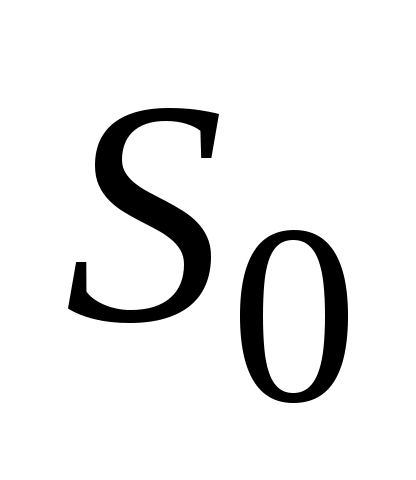 отрезка. Эта поправка всегда вводится с отрицательным знаком.
отрезка. Эта поправка всегда вводится с отрицательным знаком.
Согласно рис.2.10
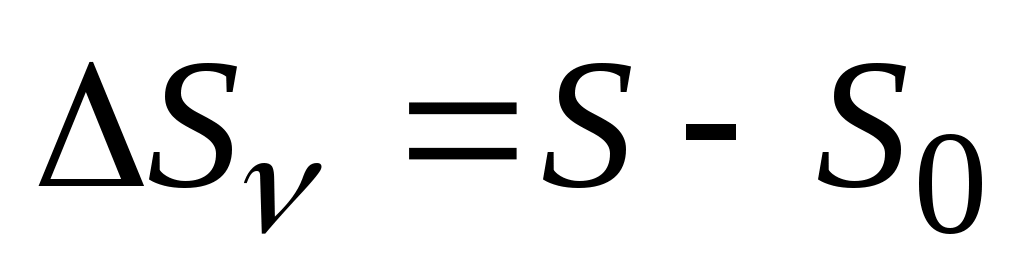 ;
; 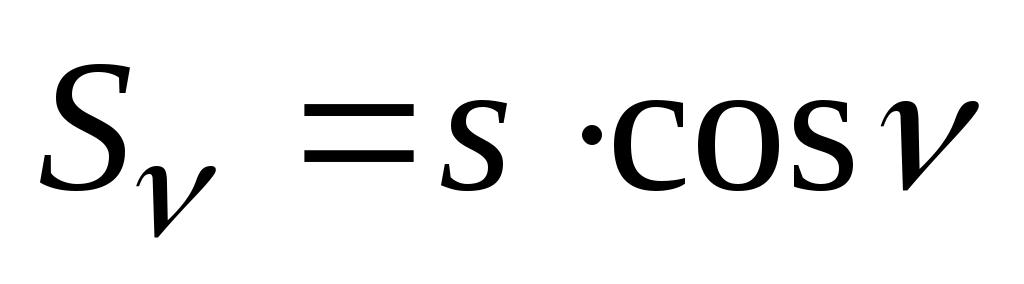 ;
;
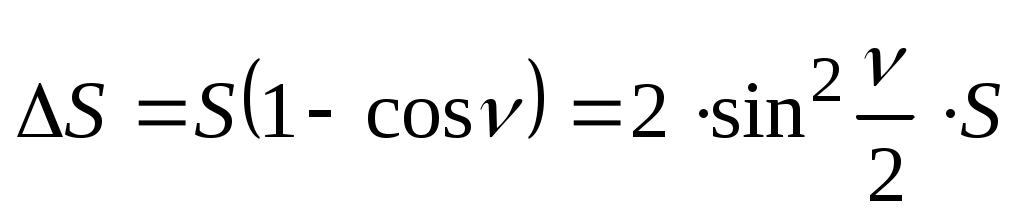 (42)
(42)
или 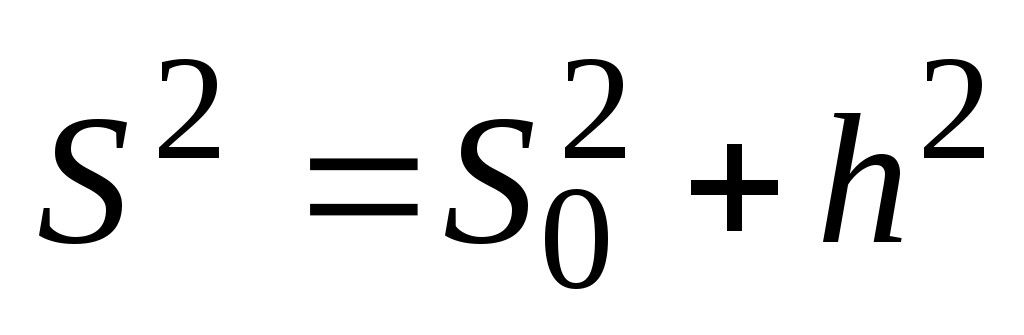 ;
; 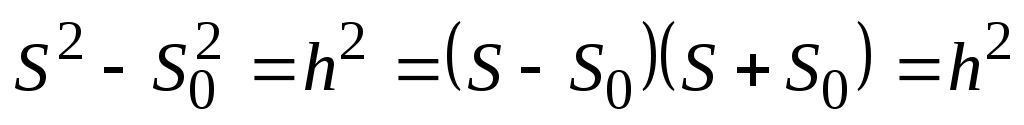 ;
; 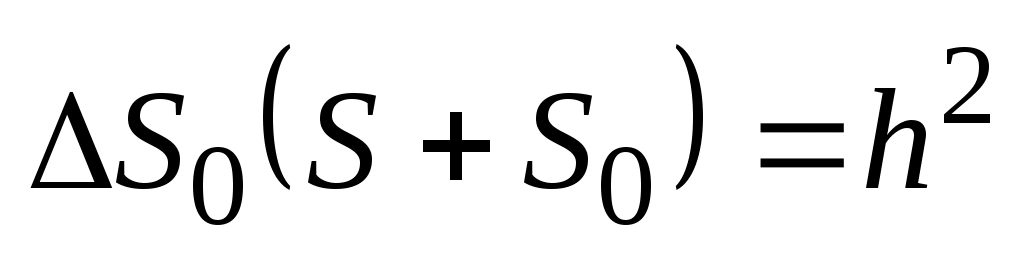 ,
,
и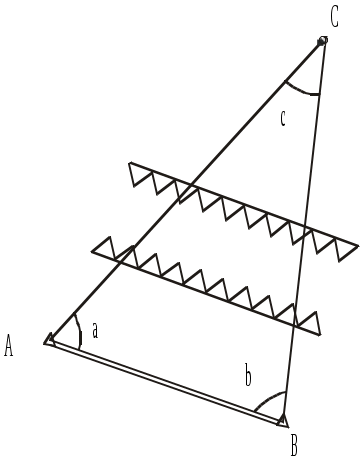 при
при 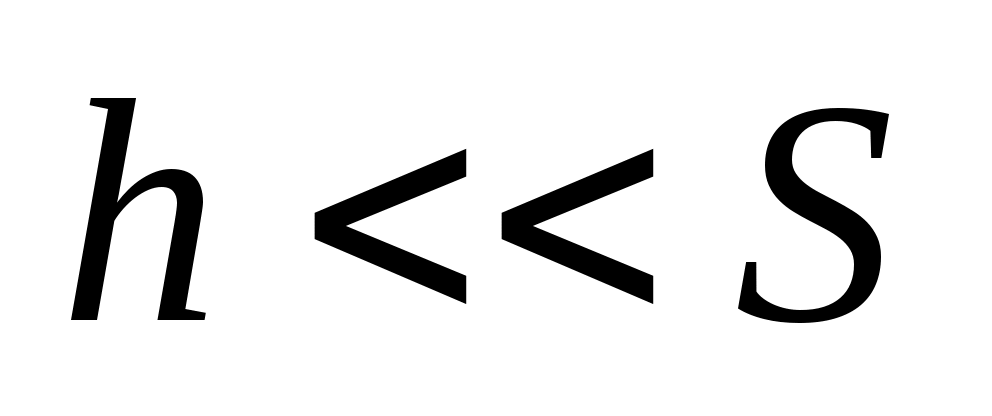
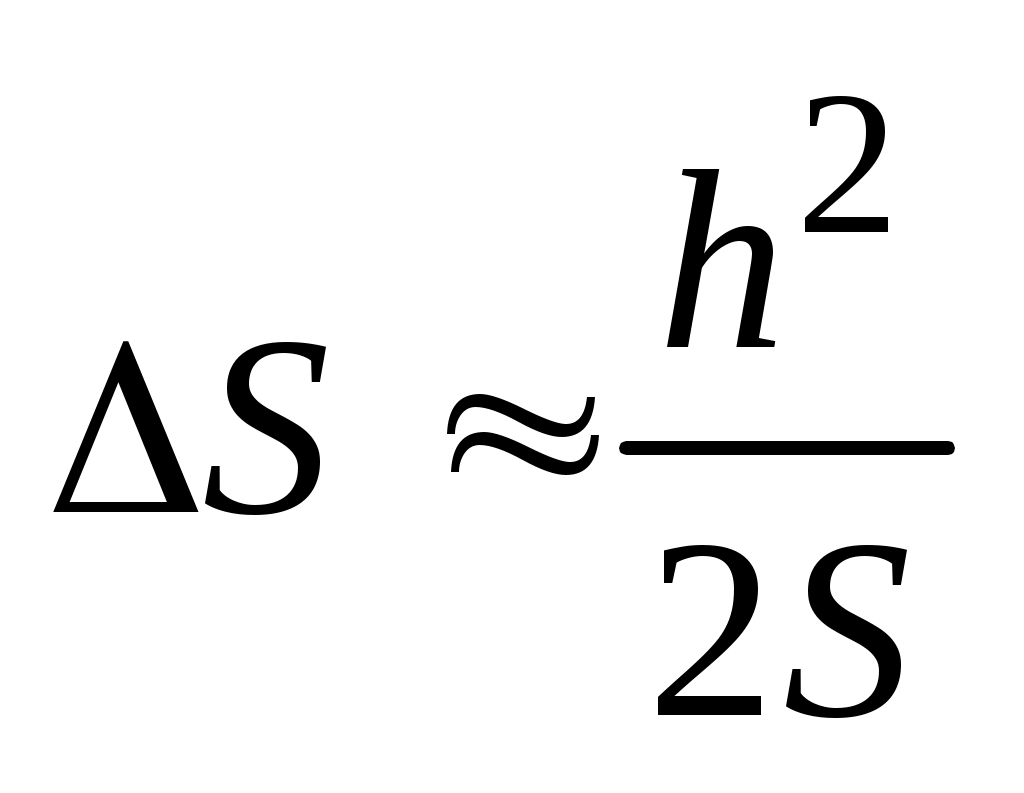 . (43)
. (43)
Е
Рис.2.11.Определение неприступного расстояния
сли непосредственное измерение линии затруднено (она проходит через овраг или водоем), то ее длину (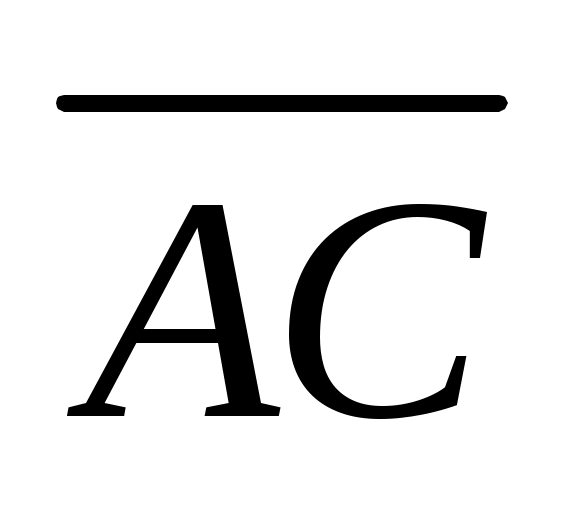 на рис.2.11) определяют косвенным путем из решения вспомогательного треугольника, в котором непосредственно измеряют базисную сторону AB и все углы. В целях большей надежности базисную сторону измеряют несколько раз и вводят в результат измерений все необходимые поправки. Тогда
на рис.2.11) определяют косвенным путем из решения вспомогательного треугольника, в котором непосредственно измеряют базисную сторону AB и все углы. В целях большей надежности базисную сторону измеряют несколько раз и вводят в результат измерений все необходимые поправки. Тогда 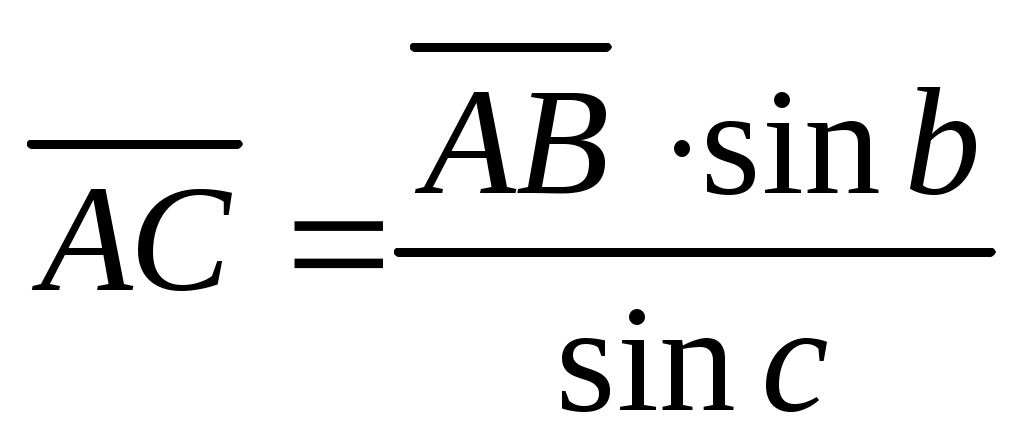 .
.
Оптические дальномеры
Принцип действия всех оптических дальномеров основан на решении параллактического треугольника (рис.2.12). В нем может быть известен (постоянен) базис b, перпендикулярный измеряемой линии, и измерен угол φ, под которым виден этот базис, или наоборот, постоянен угол φ, а измеряется базисный отрезок b. Поэтому различают два вида оптических дальномеров с постоянным углом φ или постоянным базисом:
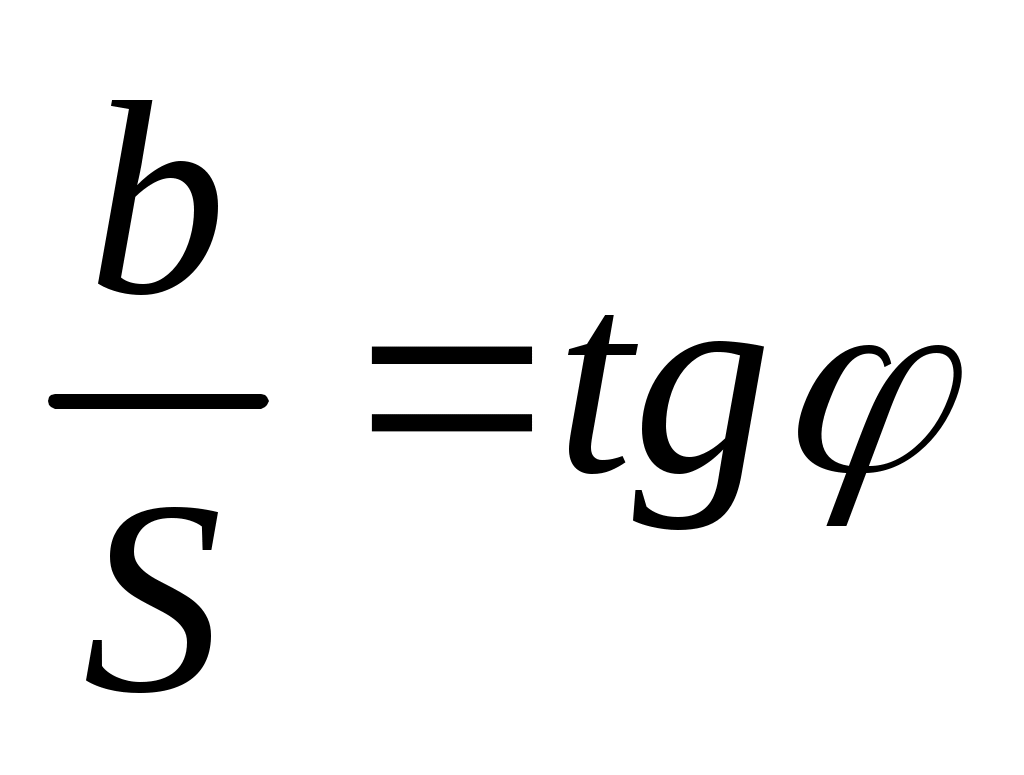
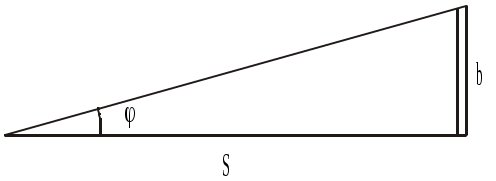 ;
; 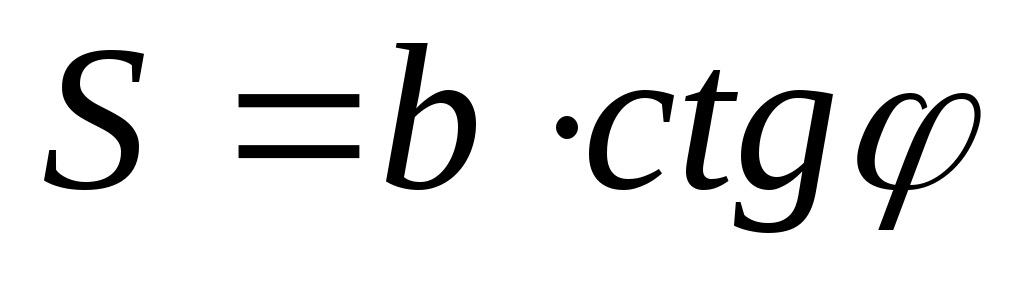 . (44)
. (44)
П
Рис.2.12. Параллактический треугольник
очти каждая зрительная труба геодезических приборов снабжена простейшим оптическим нитяным дальномером с постоянным углом φ. Сетка нитей этой трубы содержит две дополнительные нити, расстояние между которыми постоянно и равно p. Если в конечной точке линии установить вертикально рейку с сантиметровыми делениями, то глядя на нее в зрительную трубу, можно оценить базисный отрезок l, который отсекают на рейке дальномерные нити. (рис.2.13).
Этот отрезок пропорционален измеряемому расстоянию. Согласно рис.2.13 имеем 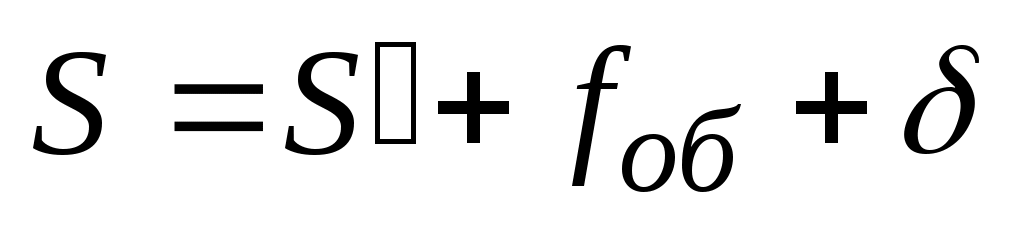 , где
, где 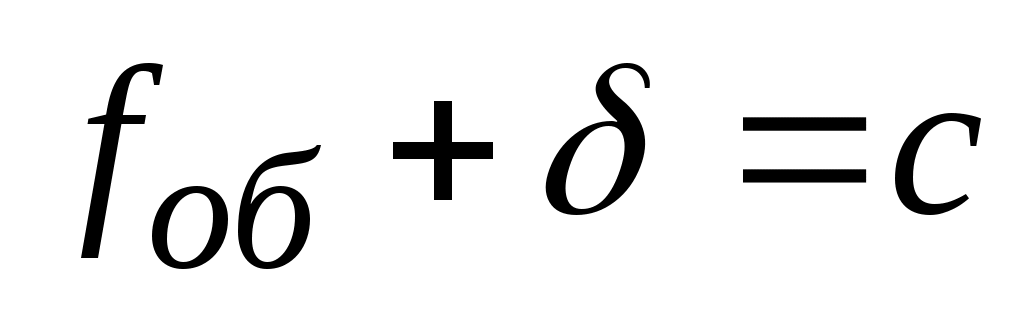 – постоянное слагаемое. Из подобия треугольников данной схемы следует:
– постоянное слагаемое. Из подобия треугольников данной схемы следует:
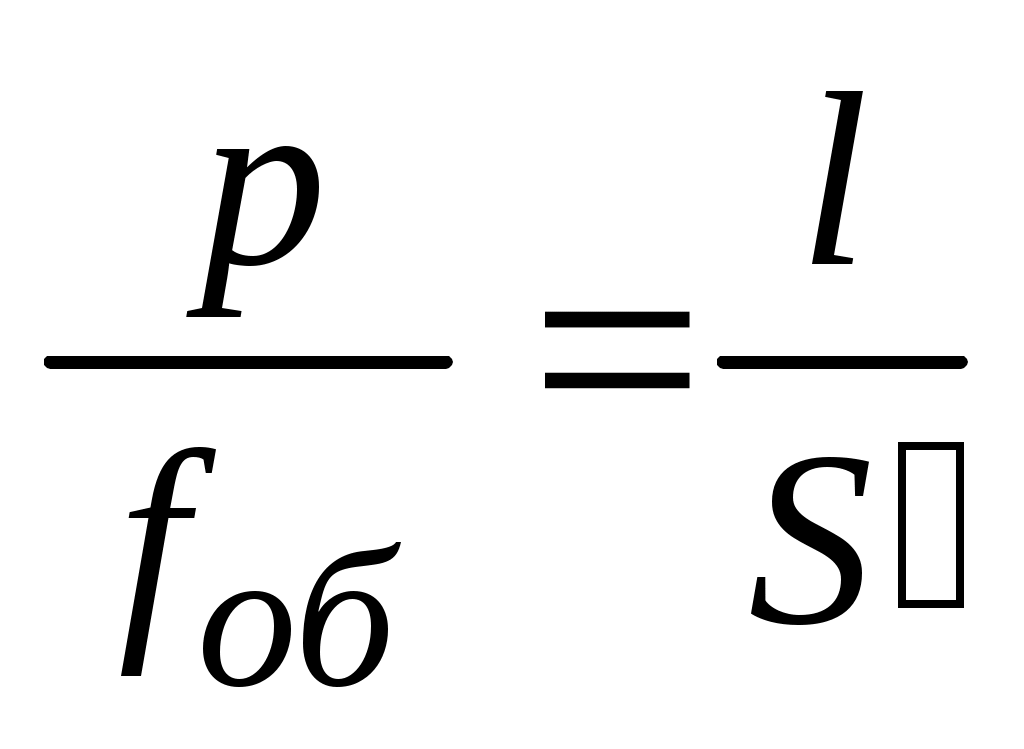 ;
; 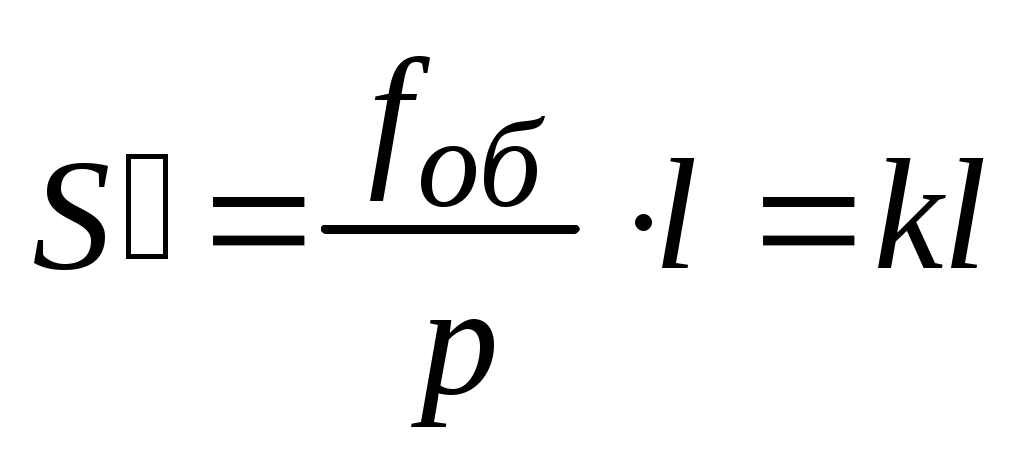 . (45)
. (45)
О
Рис.2.13. Схема нитяного дальномера
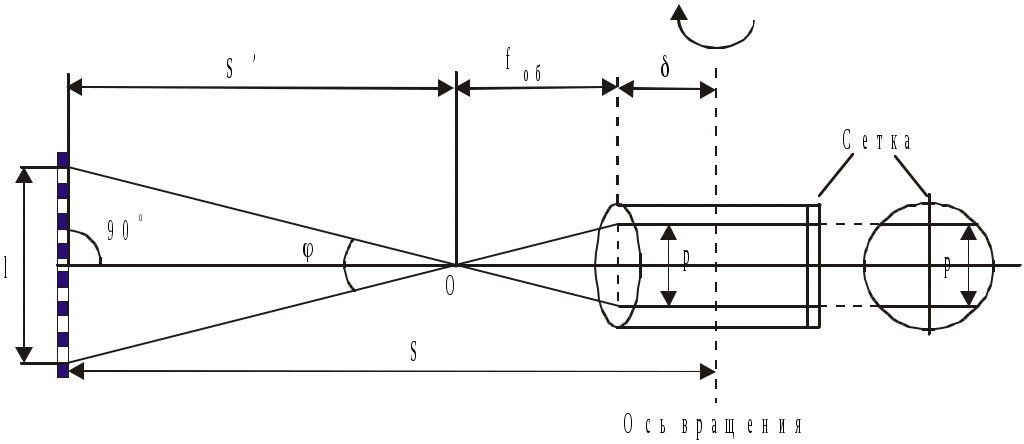
бычно в таком дальномере k = 100, а в итоге
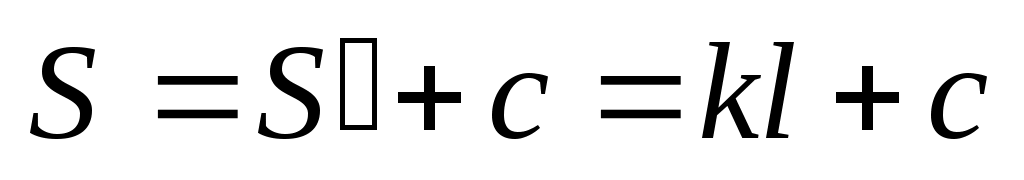 . (46)
. (46)
Последняя формула справедлива для случая, когда визирная ось зрительной трубы перпендикулярна рейке. В современных зрительных трубах с внутренним фокусированием используют более сложные оптические схемы и у них практически c = 0. Точность работы этого дальномера зависит от точности взятия отсчетов по рейке при оценке базисного отрезка l. В среднем эта точность характеризуется ошибкой в 1 – 2 мм. Однако на точность отсчета заметное влияние оказывает еще атмосферная рефракция, из–за которой визирные лучи испытывают неодинаковое искривление. Установлено, что при измерении линий нитяным дальномером относительная ошибка составляет 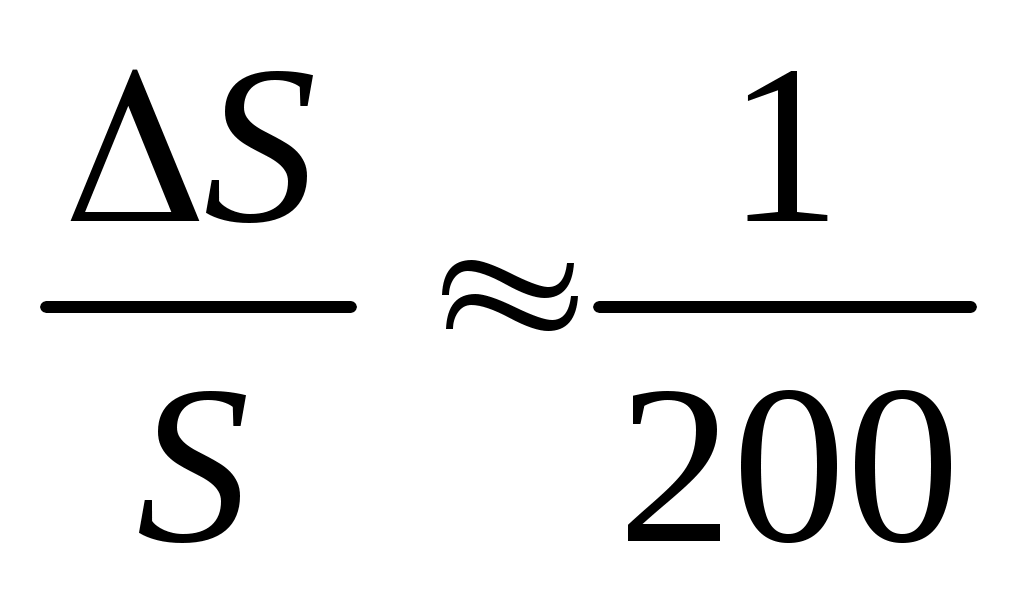 или 0,05 % от измеряемого расстояния.
или 0,05 % от измеряемого расстояния.
При определении наклонного расстояния нитяным дальномером в общем случае визирная ось трубы не перпендикулярна рейке и формула (46) видоизменяется.
На рис.2.14 дальномерные нити отсекают на рейке отрезок ab =l, а так как угол φ здесь мал ( ), то можно считать, что все визирные лучи практически параллельны. Тогда отрезок
), то можно считать, что все визирные лучи практически параллельны. Тогда отрезок 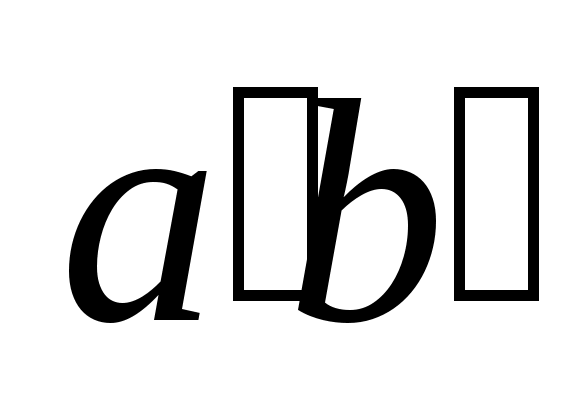 , соответствующий перпендикулярному положению рейки и визирной оси, равен
, соответствующий перпендикулярному положению рейки и визирной оси, равен 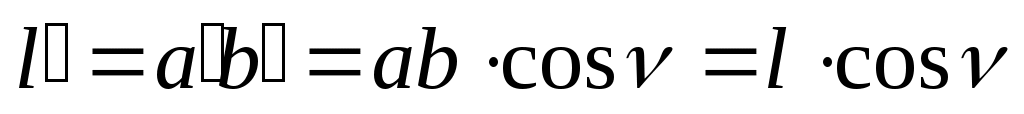 . Подставив эту величину в формулу дальномера (46), получим при c= 0:
. Подставив эту величину в формулу дальномера (46), получим при c= 0:
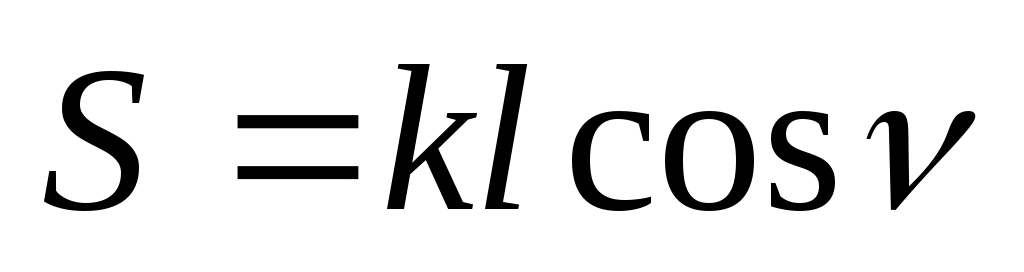 , (47)
, (47)
а горизонтальная проекция этой линии
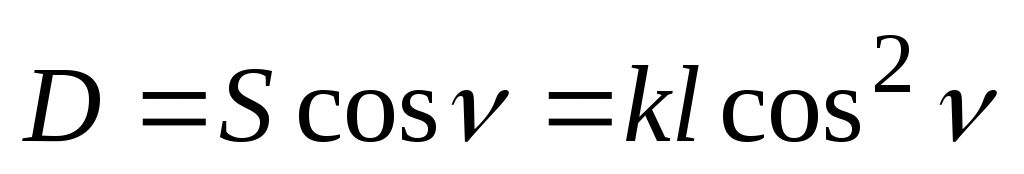 . (48)
. (48)
Ф
Рис.2.14. Определение наклонного расстояния нитяным дальномером
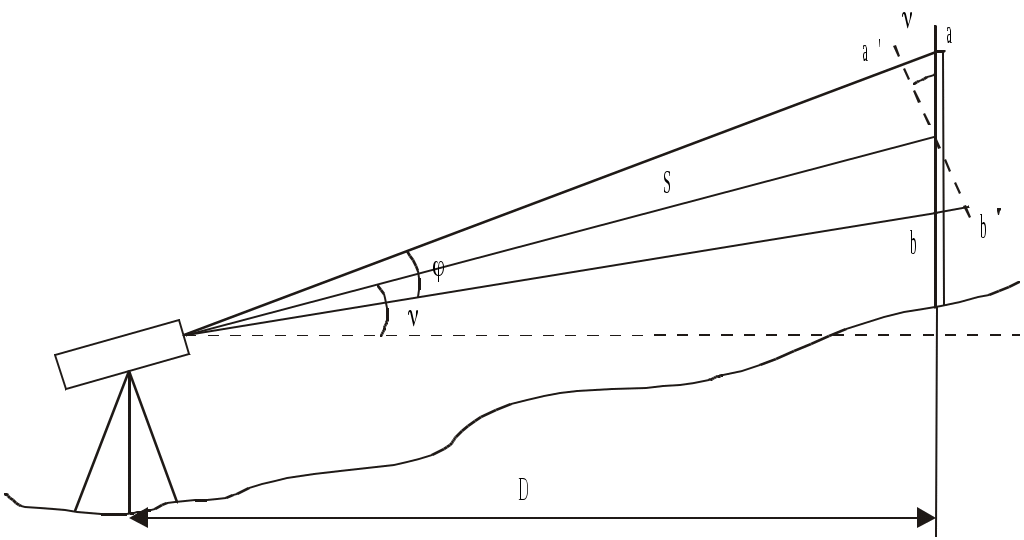
ормула справедлива для современных зрительных труб с внутренним фокусированием.
Более точные оптические дальномеры снабжены зрительными трубами двойного изображения, и в них базисный отрезок оценивается на порядок выше, чем у нитяного дальномера по величине смещения видимого изображения рейки. Эта точность заметно повышается, если рейку устанавливать горизонтально.
Д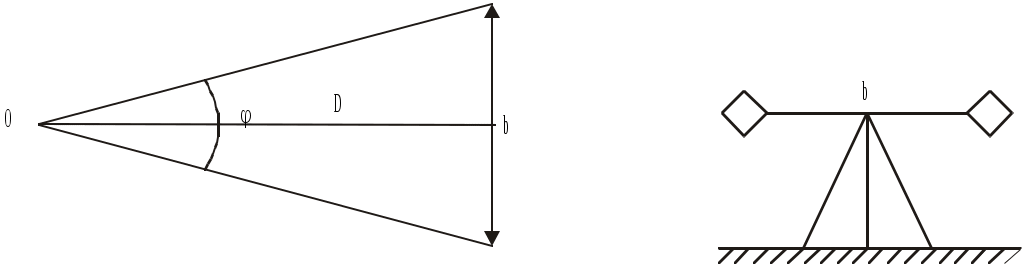
о недавнего времени на практике использовались и дальномеры с постоянным двухметровым базисом, который устанавливали перпендикулярно измеряемому расстоянию. С конца линии измерялся угол φ, под которым был виден этот базис (рис.2.15).
Рис.2.15. Дальномер с постоянным базисом
Точность работы такого дальномера зависит от точности измерения угла , так как
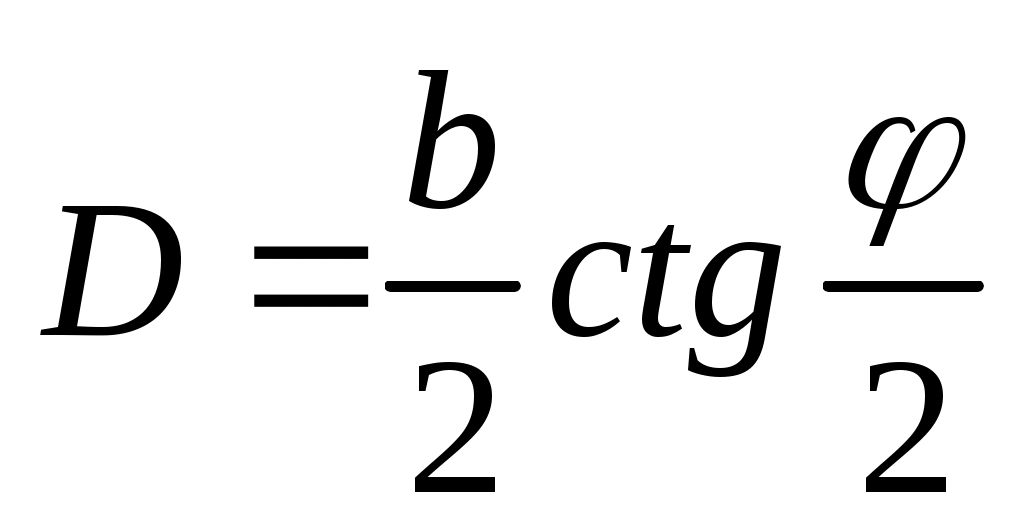 . (49)
. (49)
И здесь справедливо соотношение
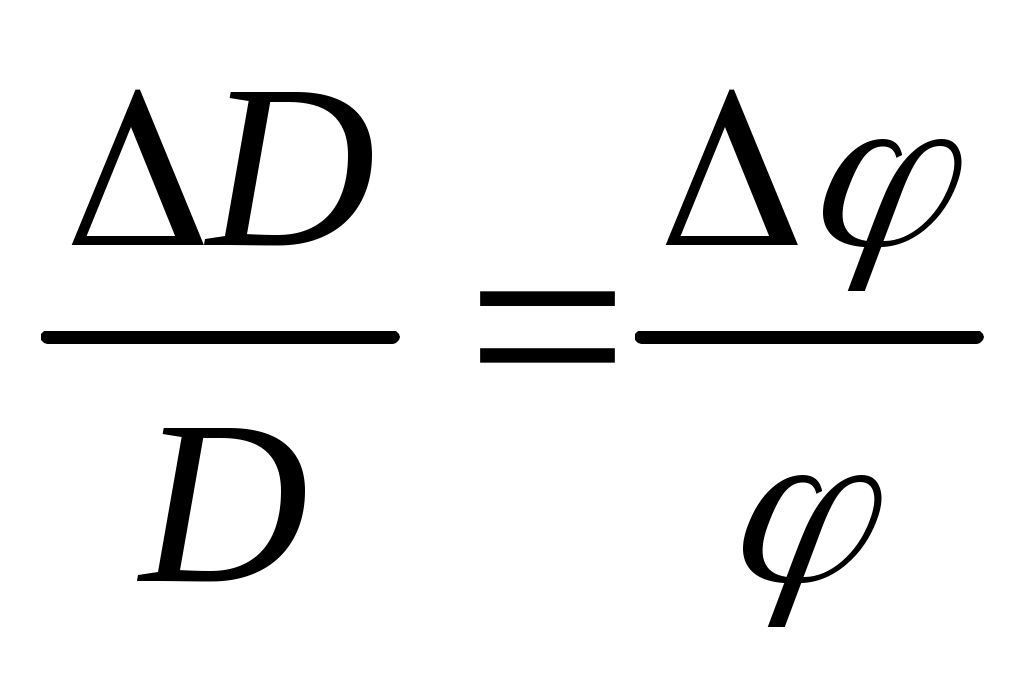 , (50)
, (50)
из которого следует, что при постоянной ошибке относительная погрешность измерения дальности уменьшается по мере увеличения угла , то есть более короткие расстояния измеряются точнее. Чтобы погрешность измерения оказалась в пределах 1/1000
1/2000, ошибка измерения угла должна быть не более 1 – 2''. Поэтому эти углы измерялись точными теодолитами Т1, Т2, либо на зрительную трубу устанавливали специальную насадку для точного измерения малых углов .
Описанный дальномер применим для измерения линий от 100 до 300 м. В настоящее время эти дальномеры вытеснены на производстве радио– и светодальномерами.
Радио– и светодальномеры
Принцип действия этих приборов основан на измерении времени t, за которое электромагнитные колебания проходят отрезок искомой линии. Такие дальномеры состоят из приемопередатчика, устанавливаемого на одном конце линии, и отражателя волн, располагаемого на другом ее конце. В процессе измерения луч света или радиоволна проходит двойное расстояние, и потому
где v– скорость распространения электромагнитных колебаний в атмосфере. Так как скорость света в вакууме c = 299792,5 км/с 3108 м/с, то чтобы добиться точности измерений хотя бы до 1 м, время t прохождения сигнала должно регистрироваться с погрешностью t<0,710–8 сек.
Современные дальномеры бывают двух видов: импульсные, в которых время t измеряют прямым путем с помощью осциллографа (в военных локаторах), и фазовые дальномеры, в которых время t находят по разности фаз поданного и принятого сигналов.
Импульсные дальномеры нашли широкое применение в космических исследованиях, а фазовые дальномеры непрерывного действия – в наземных измерениях. В этих дальномерах мерой для измерения расстояний служит длина волны модулированных электромагнитных колебаний, и искомое расстояние
где n – число уложений волн в двойном измеренном отрезке, – домер, определяемый по фазовому углу . Для решения неоднозначности при определении числа n измерения выполняют на разных частотах с известными длинами волн. Современные дальномеры снабжены счетно–решающими устройствами и световыми табло, на котором показывается результат измерений.
В измеренное расстояние вносят три поправки: за метеоусловия наблюдений, наклон линии к горизонту и постоянное слагаемое. Точность таких дальномеров характеризуется погрешностью 0,2 – 2 см.
В последнее время в строительной практике нашли применение компактные лазерные рулетки, с помощью которых бесконтактным способом (без отражателей) с достаточной точностью измеряются небольшие расстояния и размеры строительных конструкций.
Лекция 5
Измерение превышений – нивелирование

