Средний уровень запаса - основной показатель состояния запасов

Формула:

Zi= 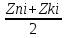, (1)

где

Zni – остаток на начало периода i;

Zki – остаток на конец периода i;



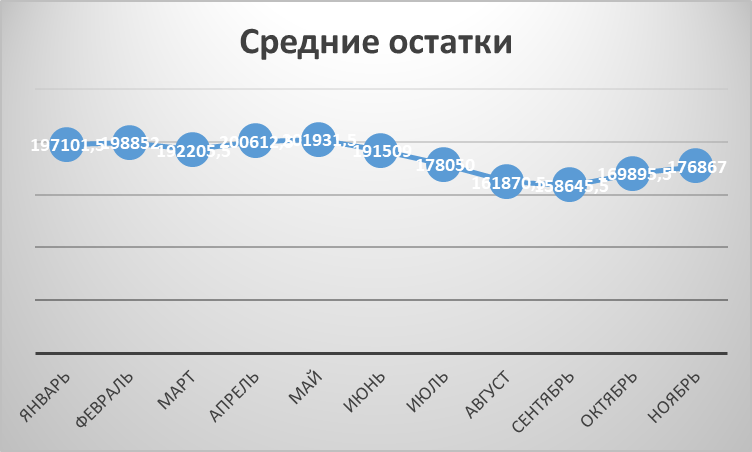
Рисунок 1 – Расчеты среднего уровня запасов

Как мы можем наблюдать на диаграмме, максимальная точка роста приходит на февраль и март, в то время как минимальная на сентябрь.
Запасоёмкость – состояние уровня запаса, показатель сколько остатков запасов приходит на ед. отгрузки приходящего периода учёта.

Zlmi ,

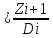(2)

где Zi – остаток запасов на начало периода i;

Di – объём отгрузки за единичный период учета i;

По результатам расчётов составим диаграмму и сопоставим результаты.



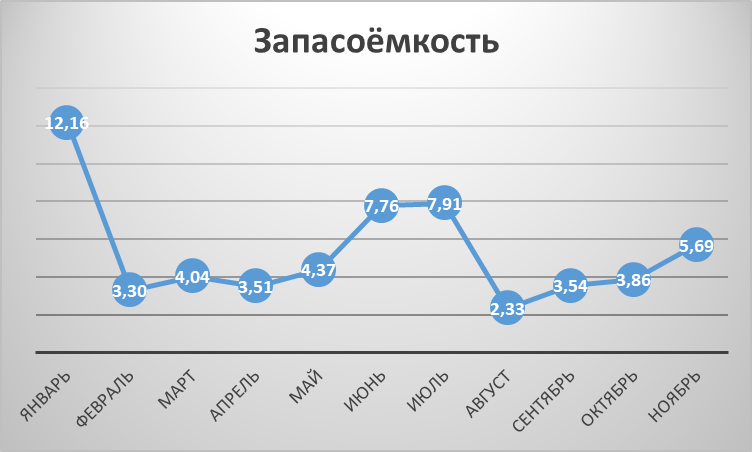
Рисунок 2 – Расчёт запасоёмкости

По результатам диаграммы можно сделать вывод , что перед новым годом и после максимальное запасоемкость достигает максимального значении после нового года она идет постепенно на убыль, с редкими подъёмами в марте, июле и октябре, но они не достигают максимума
Объём потребности запасов – имеет размерность в единицах времени

Формула:

Odi ,

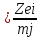(3)

где Zei – остаток запасов на конец периода учета i ед;

mj – объём отгрузок в ед. периоде j ед/дн.



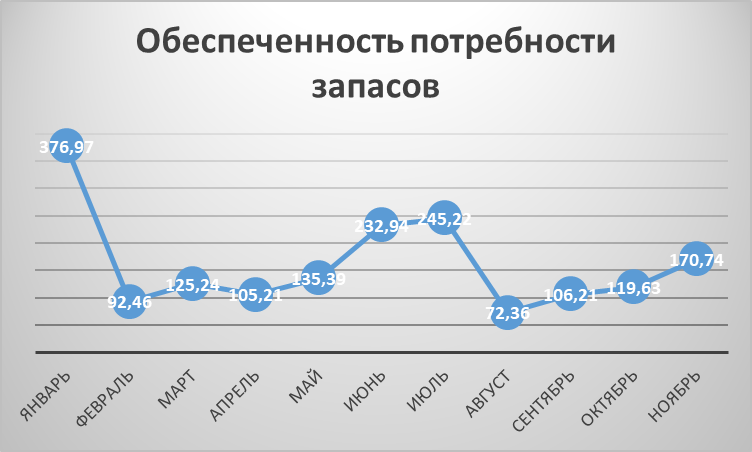
Рисунок 3 – График обеспеченности потребности запасами

Доля периода запаса – отношение объёма запаса на начало периода к предполагаемому итогу запаса на конец этого периода.



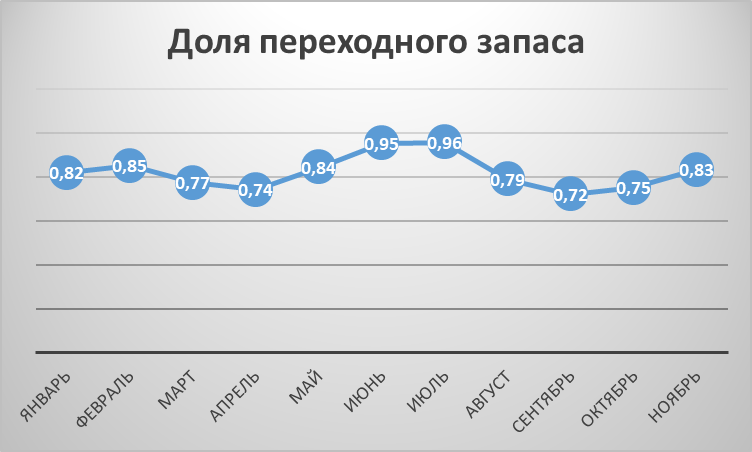
Рисунок 4 - Доля периода запаса

Показания графика указывает на постоянные скачки доли, максимальная точка приходит на май и июнь, минимальная в апреле и сентябре.

Скорость обращения запасов – показатель количества оборотов (число раз полного обновления состава среднего запаса за период i.

Формула:

Vi ,

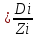(4)

где

Vi – скорость обращения, число раз;

---

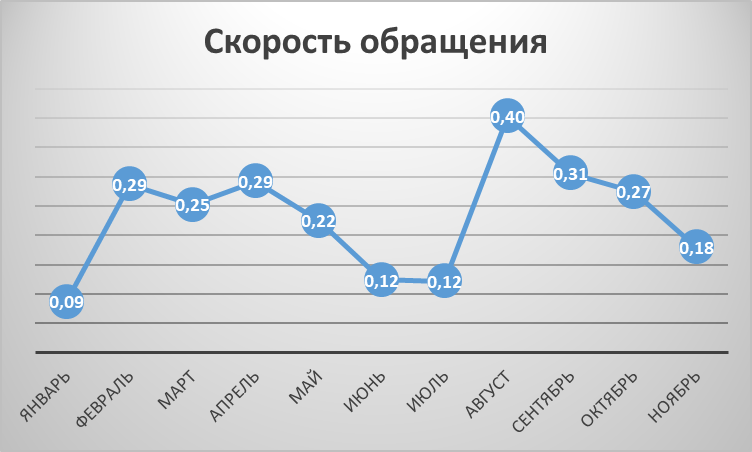
Рисунок 5 – График скорости обращения

Наблюдаются скачки скорости обращения на протяжение всего периода, так в январе и декабре минимальное скорость обращения, также в июне и юле он близится к минимальному, максимальное количество скорости обращения достигается в августе.

Время оборота – показатель среднего временного промежутка в течение которого запас находится на складе.

Формула:

Ti ,

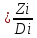(5)

где Ti – время оборота.



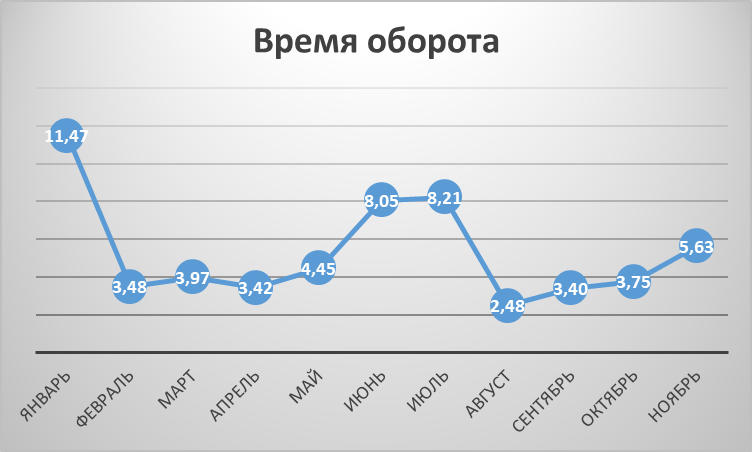
Рисунок 6 – Зависимость времени оборота от месяце

Максимальное количество времени оборота достигается в период января, декабря, также в июне и июле от достаточно высокий. Минимальное время затрачивается в феврале и августе.

2.2 Прогноз потребления запаса
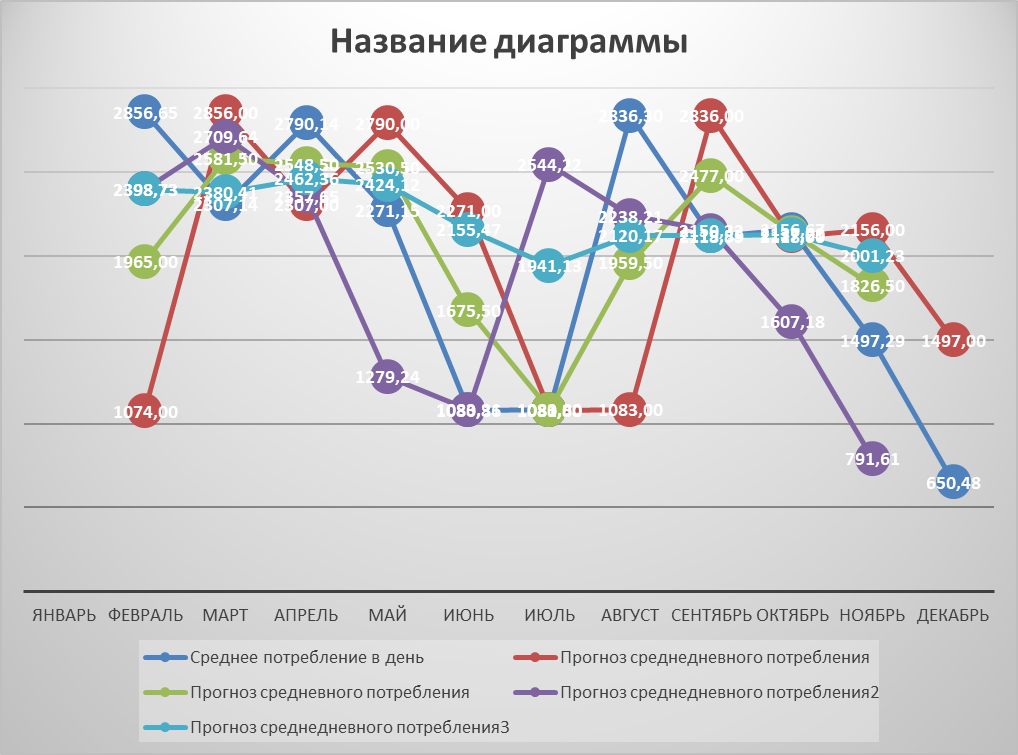
Нам известны фактические отгрузки и число рабочих дней, исходя из этих данных высчитываем среднее потребление в день и составляем прогноз методами: среднедневного потребления, среднего скользящего, среднего скользящего взвешенного и экспоненциальным методом.

Таблица 2 – Расчёт прогноза потребления запаса

Месяц	Фактические отгрузки	Наивный прогноз	Число рабочих дней	Среднее потребление в день	Прогноз среднедневного потребления	Прогноз среднемесячного потребления		Прогноз среднедневного потребления	Прогноз среднемесячного потребления
					на основе среднедневного потребления		средняя скользящая
1	2	3	4	5	6	7		8	9
Январь	17190	-	16		-	-		-	-
Февраль	57133	17190	20	2856,65	1074	21480		-	-
Март	48450	57133	21	2307,14	2856	59976		1965	41265
Апрель	58593	48450	21	2790,14	2307	48447		2581,5	54211,5
Май	45423	58593	20	2271,15	2790	55800		2548,5	50970
Июнь	23779	45423	22	1080,86	2271	49962		2530,5	55671
Июль	21676	23779	20	1083,80	1080	21600		1675,5	33510
Август	65235	21676	23	2836,30	1083	24909		1091,5	24874,5
Сентябрь	46609	65235	22	2118,59	2836	62392		1959,5	43109
Октябрь	45290	46609	21	2156,67	2118	44478		2477,00	52017
Ноябрь	31443	45290	21	1497,29	2156	45276		2137	44877
Декабрь	13660	31443	21	650,48	1497	31437		1826,5	38356,5

---

Продолжение таблицы 2

Месяц	Прогноз среднедневного потребления	Прогноз среднемесячного потребления	Прогноз среднедневного потребления	Прогноз среднемесячного потребления	Прогноз среднедневного потребления	Прогноз среднемесячного потребления
	средняя скользящая взвешенная		a=0,2		а=0,8
1	10	11	12	13	14	15
Январь	-	-	-	-	-	-
Февраль	-	-	-	-	-	-
Март	2398,73	50373,28	2398,73	50373	2398,73	50373,33
Апрель	2709,64	56902,50	2380,41	49988	2325,46	48834,67
Май	2357,65	47152,98	2462,36	49247	1953,71	39074,28
Июнь	1279,24	28143,38	2424,12	53330	2207,66	48568,58
Июль	1083,31	21666,21	2155,47	43109	1306,22	26124,47
Август	2544,22	58517,07	1941,13	44646	1128,28	25950,55
Сентябрь	2238,21	49240,62	2120,17	46643	2494,70	54883,41
Октябрь	2150,32	45156,73	2119,85	44516	2193,81	46070,07
Ноябрь	1607,18	33750,83	2127,21	44671	2164,10	45446,01
Декабрь	791,61	16623,83	2001,23	42025	1630,65	34243,60

---

Формулы:

Среднее потребление в день:

Ср.потр.д.= ;

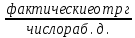(6)

Прогноз среднедневного среднемесячного потребления на основе среднедневного потребления:

П.ср.дн.потр.=

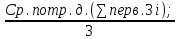
(7)

Прогноз среднедневного и среднемесячного потребления с помощью средней скользящей взвешенной:

;

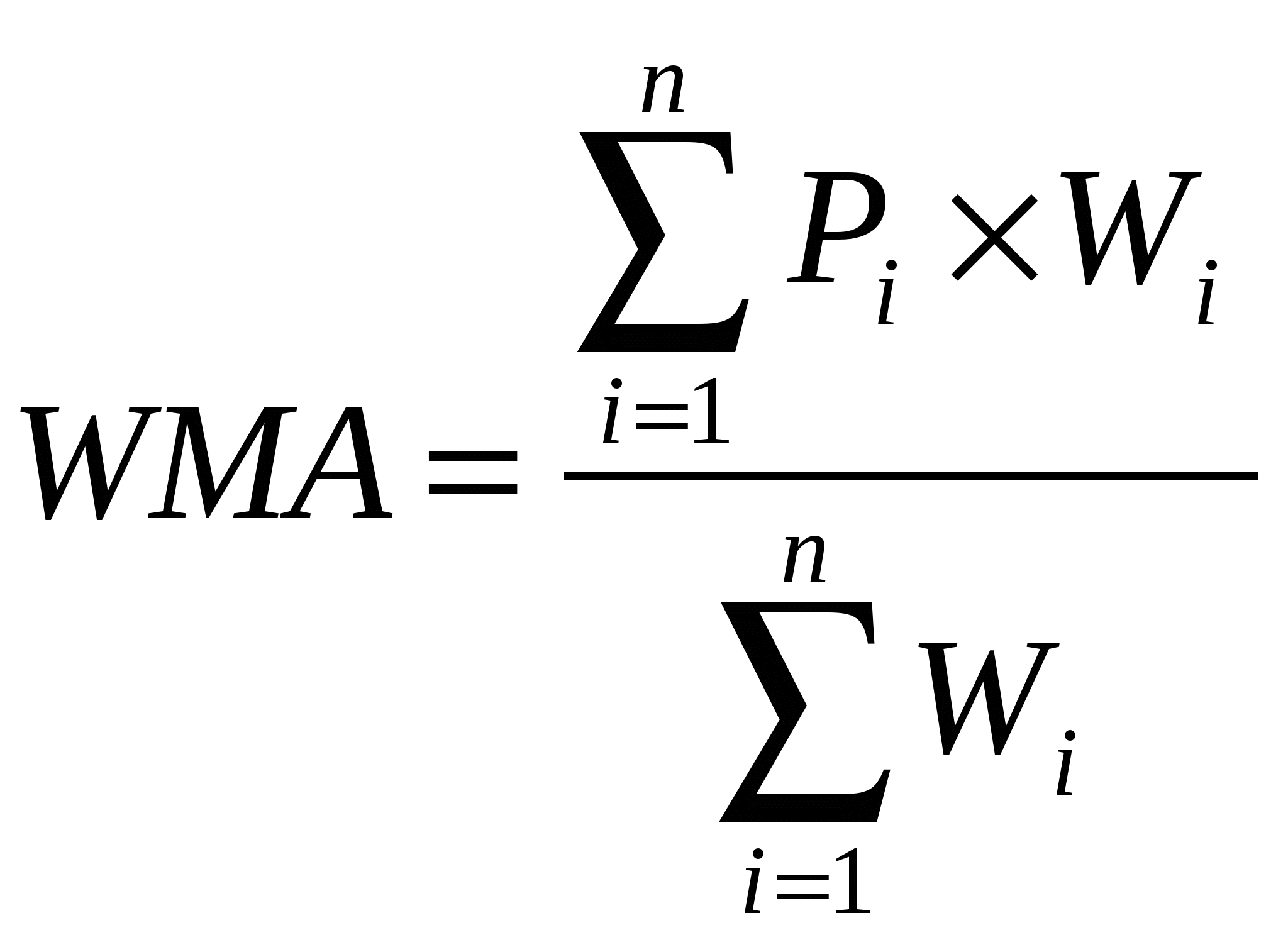(8)

где Pi – средние фактические отгрузки;

Wi – количество наблюдений.

Метод экспоненциального сглаживания наиболее эффективен при разработке среднесрочных прогнозов. Он приемлем при прогнозировании только на один период вперед. Его основные достоинства простота процедуры вычислений и возможность учета весов исходной информации. Рабочая формула метода экспоненциального сглаживания: где t – период, предшествующий прогнозному; t+1 – прогнозный период; Ut+1 - прогнозируемый показатель; α - параметр сглаживания; Уt - фактическое значение исследуемого показателя за период, предшествующий прогнозному; Ut - экспоненциально взвешенная средняя для периода, предшествующего прогнозному. 

Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.   

 

Uo - экспоненциально взвешенного среднего начального

Экспоненциальная взвешенного среднего:



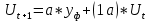
(9)

Начальное значение, через среднее арифметическое:



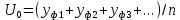
(10)

По приведенному расчету необходимо построить следующие графики для проведения анализа:



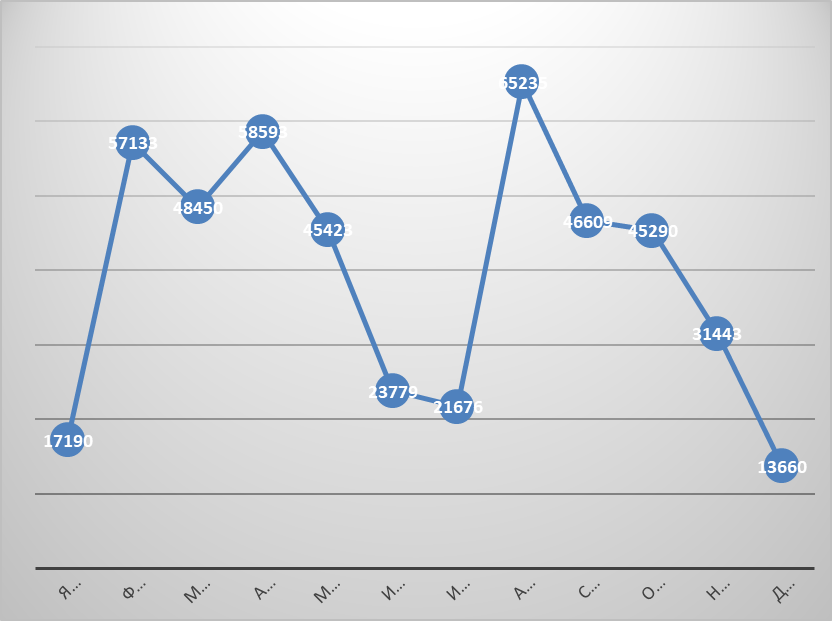
Рисунок 7 - Динамика фактических отгрузок товара по месяцам

По графику видны сильные колебания отгрузок на протяжении года. Мы наблюдаем, что минимально количество отгрузок в декабре и январе, в то время как максимальное в августе и апреле.

---

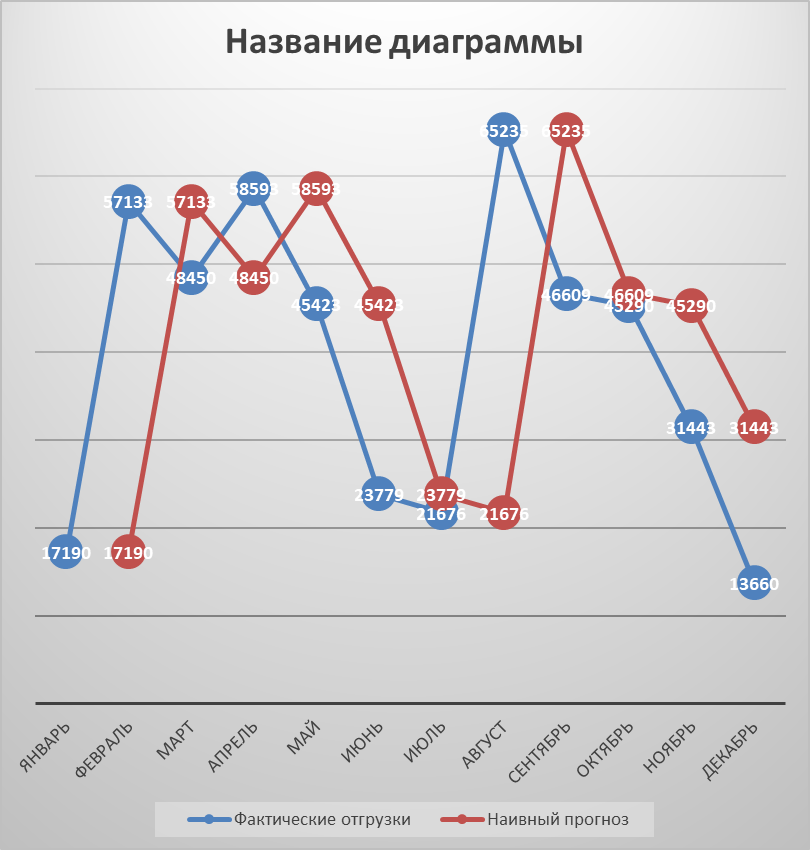
Рисунок 8 - Результаты наивного прогнозирования потребности в запасе
Наивный прогноз – применяется при наличии равномерного спроса, не имеющий сезонного периода потребления.

Заключается в том, что деятельность периода прогнозируется предыдущим периодом фактического. Достаточно прост в применении, но низкая точность. Как мы видим по графику наивный прогноз отличается от фактического и отклоняется вправо.




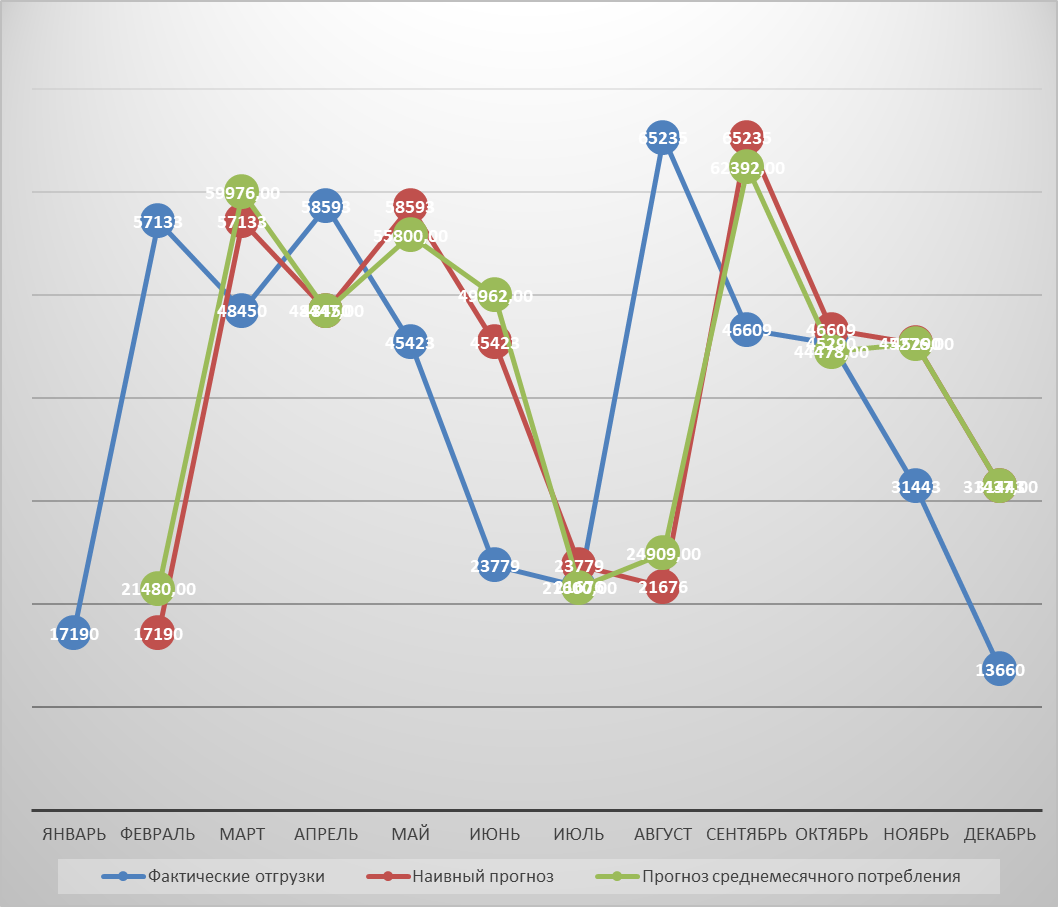
Рисунок 9 - Результаты прогнозирования потребности в запасе на основе среднедневного потребления

По графику видно что среднедневная потребность намного меньше чем фактические отгрузки и это не удивительно ведь фактические отгрузки включаются в себя показатели за весь месяц.



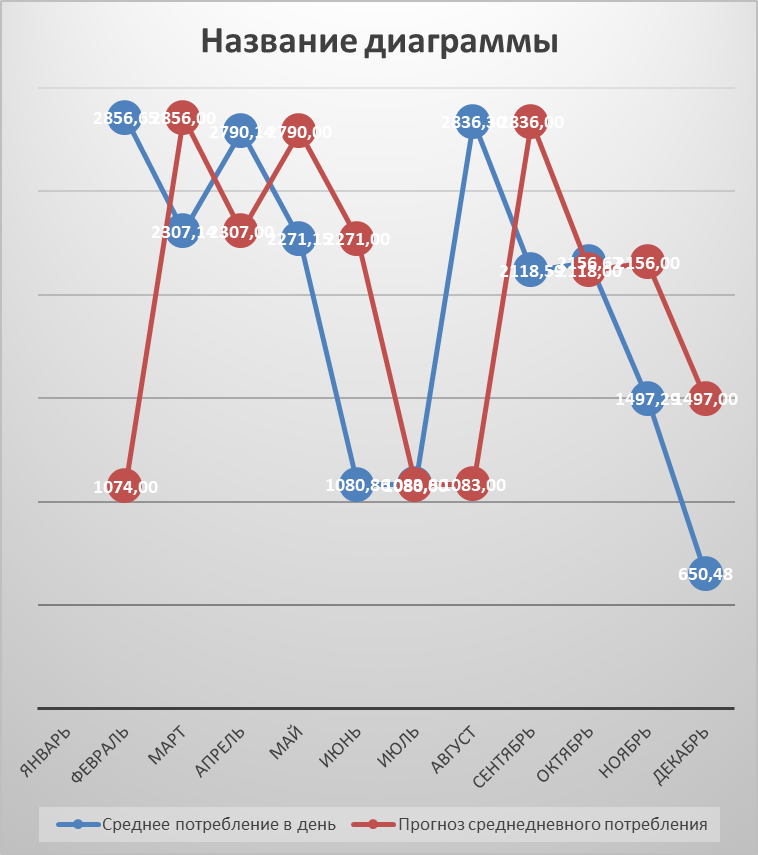
Рисунок 10 - Результаты прогнозирования потребности в запасе методом взвешенной скользящей средней

По графику видно примерно одинаковый результат, кроме скачка в сентябре, в остальные месяцы отклонение почти идентично.



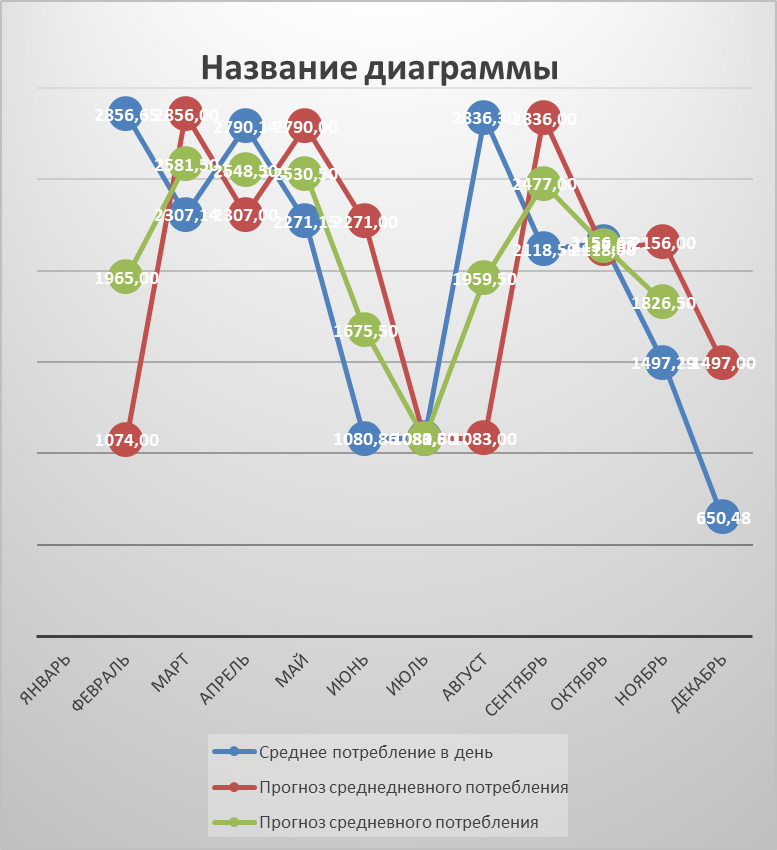
Рисунок 11 – Результаты прогнозирования потребности в запасе методом взвешенной скользящей средней и скользящей средней

По графику наблюдает идентичные тенденции между фактическими отгрузками и прогноза потребности в запасе методом взвешенной скользящей средней. В то же время скользящая средняя в сентябре даёт сильное отклонение от других прогнозов.



Рисунок 12 - Результаты прогнозирования потребности в запасе методом экспоненциального сглаживания

На графике представлены результаты расчётов экспоненциального сглаживания при значении а=0,2 и а=0,8. По результатам сравнения мы видим что они различаются так при а=0,8 фактические отгрузки примерно совпадают и составляют в большинстве месяцев более количество потребности в отличии от а=0,2.

---

Смотрите также файлы

• Лабораторная работа 1 по дисциплине Прикладная схемотехника устройств сод тема работы.docx

• Предмет биология. Класс Тема.docx

• Реферат Значение юридических категорий..docx

• Книга для тех, кто находится на перепутье и ищет компас, указывающий направление на жизнь в Потоке.pdf

• Совершенствование организационной структуры предприятия как фактор повышения эффективности деятельности (на примере ооо юта).docx