Файл: Требуется Для многопролетной балки сделать кинематический анализ и вывод о ее кинематических и статических признаках.docx

Скачать файл (0,31Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 02.02.2024

Просмотров: 24

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Вариант 11

Линейные размеры указаны в метрах.

Требуется:

1. Для многопролетной балки сделать кинематический анализ и вывод о ее кинематических и статических признаках.

2. Определить внутренние усилия от неподвижной нагрузки.

3. Определить внутренние усилия от совместного действия неподвижной и временной нагрузок (q_вр= 3,5 кН/м).

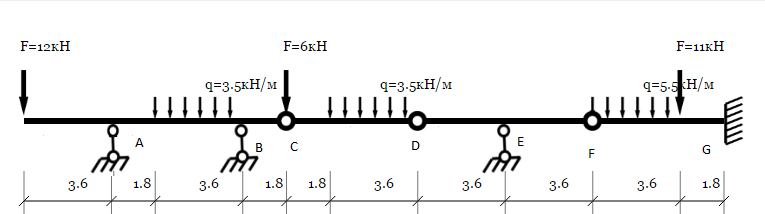
Данные к работе:

l=6 м ; P₁=6 кН ; P₂=12 кН; P₄=11 кН; q₂=3.5 кН/м ; q₄=5.5 кН/м ; q_вр=3.5 кН/м

Звено 1

Силой F₂ обозначим реакцию крайней левой опоры второго звена, отсюда F₂=10.2 кН

F₁=P₂=12 кН; q₁=q₂=3.5кН/м

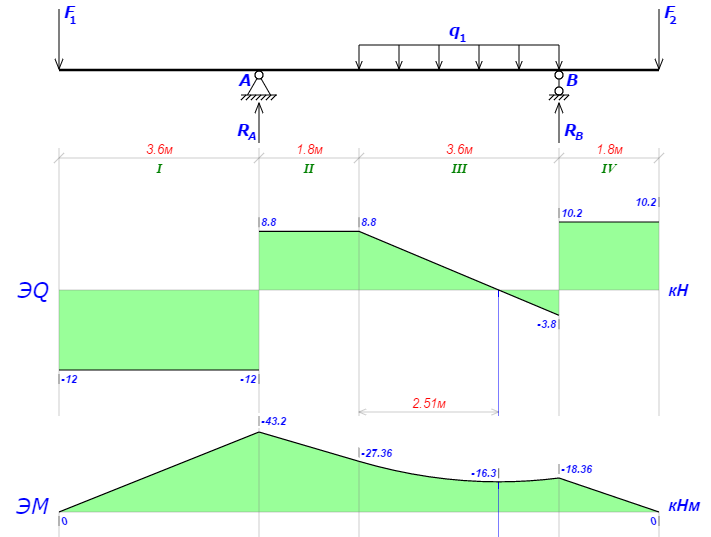
Реакции опор

Сумма моментов всех сил относительно точки B должна равняться нулю:
∑M^B = - R_A(L - L₁ - L₂) + ∑q_i(b_i - a_i)(2L - 2L₂ - a_i - b_i)/2 + ∑F_i(L - L₂ - c_i) - ∑M_i =
= - R_A(L - L₁ - L₂) + q₁(b₁ - a₁)(2L - 2L₂ - a₁ - b₁)/2 + F₁(L - L₂ - c₁) + F₂(L - L₂ - c₂) = - R_A·(10.8 - 3.6 - 1.8) + 3.5·(9 - 5.4)·(2·10.8 - 2·1.8 - 5.4 - 9)/2 + 12·(10.8 - 1.8 - 0) + 10.2·(10.8 - 1.8 - 10.8) =
= - R_A·5.4 + 3.5·3.6·1.8 + 12·9 - 10.2·1.8 =
= - R_A·5.4 + 112.32 = 0 ⇒
⇒ R_A = 112.32/5.4 = 20.8 кН;

Сумма моментов всех сил относительно точки A должна равняться нулю:
∑M^A = R_B(L - L₁ - L₂) - ∑q_i(b_i - a_i)(a_i + b_i - 2L₁)/2 - ∑F_i(c_i - L₁) - ∑M_i =
= R_B(L - L₁ - L₂) - q₁(b₁ - a₁)(a₁ + b₁ - 2L₁)/2 - F₁(c₁ - L₁) - F₂(c₂ - L₁) = R_B·(10.8 - 3.6 - 1.8) - 3.5·(9 - 5.4)·(5.4 + 9 - 2·3.6)/2 - 12·(0 - 3.6) - 10.2·(10.8 - 3.6) =
= R_B·5.4 - 3.5·3.6·3.6 - 12·3.6 - 10.2·7.2 =

= R_B·5.4 - 75.6 = 0 ⇒
⇒ R_B = 75.6/5.4 = 14 кН;

Для проверки вычислим сумму проекций всех сил на вертикальную ось:
∑Y = R_A + R_B - ∑q_i(b_i - a_i) - ∑F_i =
= R_A + R_B - q₁(b₁ - a₁) - F₁ - F₂ =
= 20.8 + 14 - 3.5·(9 - 5.4) - 12 - 10.2 =
= 20.8 + 14 - 12.6 - 12 - 10.2 = 0;

Построение эпюр

Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках.

Участок I (0 ≤ z ≤ 3.6):

Поперечная сила Q:
Q_I(z) = - F₁ =
= -12;

Значения Q на краях отрезка:
Q_I(0) = -12 кН;
Q_I(3.6) = -12 кН;

Изгибающий момент M:
M_I(z) = - F₁(z - c₁) = - 12(z - 0) =
= -12z;

Значения M на краях отрезка:
M_I(0) = -12·0 = 0;
M_I(3.6) = -12·3.6 = -43.2 кНм;

Участок II (3.6 ≤ z ≤ 5.4):

Поперечная сила Q:
Q_II(z) = R_A - F₁ = 20.8 - 12 =
= 8.8;

Значения Q на краях отрезка:
Q_II(3.6) = 8.8 кН;
Q_II(5.4) = 8.8 кН;

Изгибающий момент M:
M_II(z) = R_A(z - L₁) - F₁(z - c₁) = 20.8(z - 3.6)- 12(z - 0) =
= 8.8z - 74.88;

Значения M на краях отрезка:
M_II(3.6) = 8.8·3.6 - 74.88 = -43.2 кНм;
M_II(5.4) = 8.8·5.4 - 74.88 = -27.36 кНм;

Участок III (5.4 ≤ z ≤ 9):

Поперечная сила Q:
Q_III(z) = R_A - q₁(z - a₁) - F₁ = 20.8 - 3.5(z - 5.4) - 12 =
= -3.5z + 27.7;

Значения Q на краях отрезка:
Q_III(5.4) = -3.5·5.4 + 27.7 = 8.8 кН;
Q_III(9) = -3.5·9 + 27.7 = -3.8 кН;

На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения:
Q_III(z) = -3.5z + 27.7 = 0 ⇒
⇒ z₁ = 27.7/3.5 = 7.91429 м;

Изгибающий момент M:
M_III(z) = R_A(z - L₁) - q₁(z - a₁)²/2 - F₁(z - c₁) = 20.8(z - 3.6)- 3.5(z - 5.4)²/2 - 12(z - 0) = 20.8(z - 3.6)- 3.5(z²/2 - 5.4z + 14.58) - 12z =
= -1.75z² + 27.7z - 125.91;

Значения M на краях отрезка:
M_III(5.4) = -1.75·5.4² + 27.7·5.4 - 125.91 = -27.36 кНм;
M_III(9) = -1.75·9² + 27.7·9 - 125.91 = -18.36 кНм;

Локальный экстремум в точке z₁ = 7.91429 м:
M_III(7.91429) = -1.75·7.91429² + 27.7·7.91429 - 125.91 = -16.2971 кНм;

Участок IV (9 ≤ z ≤ 10.8):

Поперечная сила Q:
Q_IV(z) = R_A + R_B - q₁(z - a₁) + q₁(z - b₁) - F₁ = 20.8 + 14 - 3.5(z - 5.4) + 3.5(z - 9) - 12 =
= 10.2;

Значения Q на краях отрезка:
Q_IV(9) = 10.2 кН;
Q_IV(10.8) = 10.2 кН;

Изгибающий момент M:
M_IV(z) = R_A(z - L₁) + R_B(z - L + L₂) - q₁(z - a₁)²/2 + q₁(z - b₁)²/2 - F₁(z - c₁) = 20.8(z - 3.6)+ 14(z - 10.8 + 1.8) - 3.5(z - 5.4)²/2 + 3.5(z - 9)²/2 - 12(z - 0) = 20.8(z - 3.6)+ 14(z - 9) - 3.5(z²/2 - 5.4z + 14.58) + 3.5(z²/2 - 9z + 40.5) - 12z =
= 10.2z - 110.16;

Значения M на краях отрезка:
M_IV(9) = 10.2·9 - 110.16 = -18.36 кНм;
M_IV(10.8) = 10.2·10.8 - 110.16 = 0;

Звено 2

F₁=P₁=6 кН; q₁=q₂=3.5кН/м

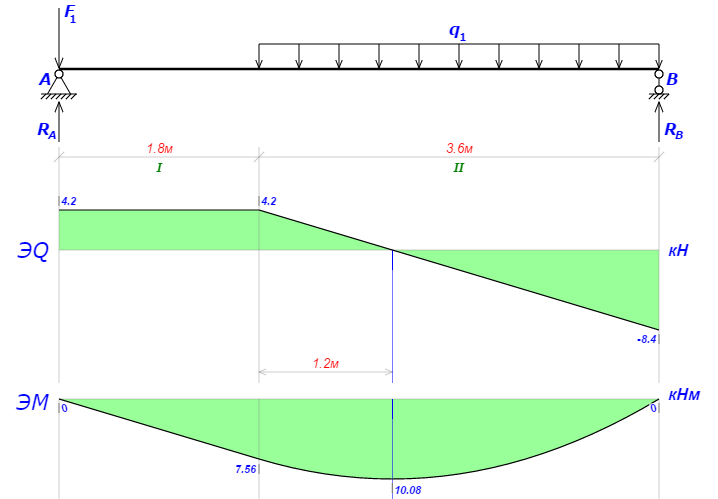
Реакции опор

Сумма моментов всех сил относительно точки B должна равняться нулю:
∑M^B = - R_A L + ∑q_i(b_i - a_i)(2L - a_i - b_i)/2 + ∑F_i(L - c_i) - ∑M_i =
= - R_A L + q₁(b₁ - a₁)(2L - a₁ - b₁)/2 + F₁(L - c₁) = - R_A·5.4 + 3.5·(5.4 - 1.8)·(2·5.4 - 1.8 - 5.4)/2 + 6·(5.4 - 0) =
= - R_A·5.4 + 3.5·3.6·1.8 + 6·5.4 =
= - R_A·5.4 + 55.08 = 0 ⇒
⇒ R_A = 55.08/5.4 = 10.2 кН;

Сумма моментов всех сил относительно точки A должна равняться нулю:
∑M^A = R_B L - ∑q_i(b_i - a_i)(a_i + b_i)/2 - ∑F_ic_i - ∑M_i =
= R_B L - q₁(b₁ - a₁)(a₁ + b₁)/2 - F₁c₁ = R_B·5.4 - 3.5·(5.4 - 1.8)·(1.8 + 5.4)/2 - 6·0 =
= R_B·5.4 - 3.5·3.6·3.6 + 6·0 =
= R_B·5.4 - 45.36 = 0 ⇒
⇒ R_B = 45.36/5.4 = 8.4 кН;

Для проверки вычислим сумму проекций всех сил на вертикальную ось:
∑Y = R_A + R_B - ∑q_i(b_i - a_i

) - ∑F_i =
= R_A + R_B - q₁(b₁ - a₁) - F₁ =
= 10.2 + 8.4 - 3.5·(5.4 - 1.8) - 6 =
= 10.2 + 8.4 - 12.6 - 6 = 0;

Построение эпюр

Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках.

Участок I (0 ≤ z ≤ 1.8):

Поперечная сила Q:
Q_I(z) = R_A - F₁ = 10.2 - 6 =
= 4.2;

Значения Q на краях отрезка:
Q_I(0) = 4.2 кН;
Q_I(1.8) = 4.2 кН;

Изгибающий момент M:
M_I(z) = R_A z - F₁(z - c₁) = 10.2z - 6(z - 0) =
= 4.2z;

Значения M на краях отрезка:
M_I(0) = 4.2·0 = 0;
M_I(1.8) = 4.2·1.8 = 7.56 кНм;

Участок II (1.8 ≤ z ≤ 5.4):

Поперечная сила Q:
Q_II(z) = R_A - q₁(z - a₁) - F₁ = 10.2 - 3.5(z - 1.8) - 6 =
= -3.5z + 10.5;

Значения Q на краях отрезка:
Q_II(1.8) = -3.5·1.8 + 10.5 = 4.2 кН;
Q_II(5.4) = -3.5·5.4 + 10.5 = -8.4 кН;

На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения:
Q_II(z) = -3.5z + 10.5 = 0 ⇒
⇒ z₁ = 10.5/3.5 = 3 м;

Изгибающий момент M:
M_II(z) = R_A z - q₁(z - a₁)²/2 - F₁(z - c₁) = 10.2z - 3.5(z - 1.8)²/2 - 6(z - 0) = 10.2z - 3.5(z²/2 - 1.8z + 1.62) - 6z =
= -1.75z² + 10.5z - 5.67;

Значения M на краях отрезка:
M_II(1.8) = -1.75·1.8² + 10.5·1.8 - 5.67 = 7.56 кНм;
M_II(5.4) = -1.75·5.4² + 10.5·5.4 - 5.67 = 0;

Локальный экстремум в точке z₁ = 3 м:
M_II(3) = -1.75·3² + 10.5·3 - 5.67 = 10.08 кНм;

Звено 3

Силой F₁= 8,4 кН обозначим реакцию крайней правой опоры второго звена

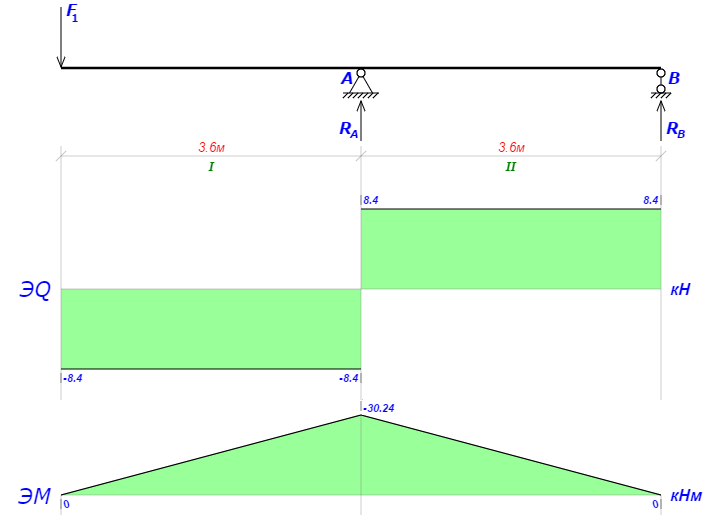
Реакции опор

Сумма моментов всех сил относительно точки B должна равняться нулю:
∑M^B = - R_A(L - L₁) + ∑q_i(b_i - a_i)(2L - a_i - b_i)/2 + ∑F_i(L

- c_i) - ∑M_i =
= - R_A(L - L₁) + F₁(L - c₁) = - R_A·(7.2 - 3.6) + 8.4·(7.2 - 0) =
= - R_A·3.6 + 8.4·7.2 =
= - R_A·3.6 + 60.48 = 0 ⇒
⇒ R_A = 60.48/3.6 = 16.8 кН;

Сумма моментов всех сил относительно точки A должна равняться нулю:
∑M^A = R_B(L - L₁) - ∑q_i(b_i - a_i)(a_i + b_i - 2L₁)/2 - ∑F_i(c_i - L₁) - ∑M_i =
= R_B(L - L₁) - F₁(c₁ - L₁) = R_B·(7.2 - 3.6) - 8.4·(0 - 3.6) =
= R_B·3.6 - 8.4·3.6 =
= R_B·3.6 + 30.24 = 0 ⇒
⇒ R_B = -30.24/3.6 = -8.4 кН;

Для проверки вычислим сумму проекций всех сил на вертикальную ось:
∑Y = R_A + R_B - ∑q_i(b_i - a_i) - ∑F_i =
= R_A + R_B - F₁ =
= 16.8 - 8.4 - 8.4 = 0;

Построение эпюр

Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках.

Участок I (0 ≤ z ≤ 3.6):

Поперечная сила Q:
Q_I(z) = - F₁ =
= -8.4;

Значения Q на краях отрезка:
Q_I(0) = -8.4 кН;
Q_I(3.6) = -8.4 кН;

Изгибающий момент M:
M_I(z) = - F₁(z - c₁) = - 8.4(z - 0) =
= -8.4z;

Значения M на краях отрезка:
M_I(0) = -8.4·0 = 0;
M_I(3.6) = -8.4·3.6 = -30.24 кНм;

Участок II (3.6 ≤ z ≤ 7.2):

Поперечная сила Q:
Q_II(z) = R_A - F₁ = 16.8 - 8.4 =
= 8.4;

Значения Q на краях отрезка:
Q_II(3.6) = 8.4 кН;
Q_II(7.2) = 8.4 кН;

Изгибающий момент M:
M_II(z) = R_A(z - L₁) - F₁(z - c₁) = 16.8(z - 3.6)- 8.4(z - 0) =
= 8.4z - 60.48;

Значения M на краях отрезка:
M_II(3.6) = 8.4·3.6 - 60.48 = -30.24 кНм;
M_II(7.2) = 8.4·7.2 - 60.48 = 0;

Звено 4

Силой F1=-8.4 кН обозначим реакцию крайней правой опоры третьего звена

Смотрите также файлы

Проблемы исторического познания. Формационный и цивилизационный подходы к истории, их сущность и познавательный потенциал.docx

Методические указания по выполнению лабораторных работ для студентов очной формы обучения. Псков, Издво ПсковГУ, 2017. 50 с.doc

20222023 уч г. Мониторинг образовательных достижений обучающихся.docx

Программа соревнований.docx

Утверждаю Начальник пч65 Ю. А. Медведев 20 г. Методический план.doc

Файл: Требуется Для многопролетной балки сделать кинематический анализ и вывод о ее кинематических и статических признаках.docx

Смотрите также файлы

Информация

Списки файлов

Дополнительно