Задания и методические указания к выполнению ПРАКТИЧЕСКИХ зАДАЧ
1.1 Методические указания по выполнению практических задач. Примеры решения задач

1. 
   Основные показатели риска в инвестировании капитала.
   

Пример №1. Имеются два варианта вложений одной и той же суммы капитала. При первом варианте капитал совершает за год 20 оборотов, рентабельность произведенного и реализованного товара 20%. По второму варианту капитал совершает за год 26 оборотов, рентабельность произведенного и реализованного товара 18%. Выбор эффективного варианта вложения капитала производится по критерию – максимум нормы прибыли на капитал.

При перспективных вложениях капитала оценивается величина капитала со степенью риска.

Степень риска при венчурном капитале может выражаться различными показателями, например капиталоотдачей и рентабельностью капитала.

Капиталоотдача, или скорость обращения капитала, определяется отношением объема выручки к вложенному капиталу и выражается числом оборотов:
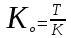, (1)

где Ко – капиталоотдача, обороты;

Т - выручка, получаемая от использования вложенного капитала за определенный период (обычно год);

К – сумма вложенного капитала.
Рентабельность капитала, или норма прибыли на вложенный капитал, определяется процентным отношением прибыли к капиталу:
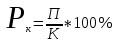, (2)

где Рк – рентабельность капитала (норма прибыли на вложенный капитал), %;

П – сумма прибыли, получаемая от использования вложенного капитала за определенный период (обычно год);

К – сумма вложенного капитала.
Норма прибыли – интегральный показатель, состоящий из произведения двух показателей: капиталоотдачи и рентабельности произведенной и реализованной продукции.

Рентабельность произведенного и реализованного товара измеряется процентным отношением прибыли к объему выручки:
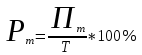, (3)

где Рт – рентабельность

---

произведенного и реализованного товара, %;

П – прибыль, полученная от производства и реализации товара (т.е. от использования вложенного капитала) за определенный период.
Связь между приведенными показателями выражается формулами:

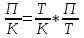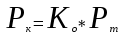или . (4)
Решение:

По первому варианту:



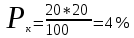
По второму варианту



Выбран второй вариант, как более рентабельный.

2. 
   Оценка степени риска.
   

Пример №2.Имеются два варианта вложения капитала. Установлено, что при вложении капитала в мероприятие А получение прибыли в сумме 25 млн. тенге имеет вероятность 0,6, а в мероприятие Б получение прибыли в сумме 30 млн. тенге имеет вероятность 0,4. Тогда ожидаемое получение прибыли от вложения капитала (математическое ожидание) составит:

- по мероприятию А – 25*0,6 = 15 млн. тенге

- по мероприятию Б – 30*0,4 = 12 млн. тенге

Таким образом выбирается вариант А, где ожидаемое получение прибыли с учетом его вероятности – наибольшее.

Вероятность может быть оценена двумя способами:

1. 
   Объективный метод оценки вероятности.
   

Вероятность вычисляется как частота, с которой происходит данное событие. Если известно, что при вложении капитала в конкретное мероприятие была получена прибыль в сумме 25 млн. тенге в 120 случаях из 200, то вероятность получения прибыли составляет 0,6 (120/200) или 60% ((120*100%)/200).

2. 
   Субъективный метод оценки вероятности.
   

Используются субъективные критерии, которые базируются на различных предположениях. Предположения могут основываться на суждении оценивающего, его личном опыте, оценке эксперта, мнении финансового консультанта и др. Применяется метод экспертной оценки.
1.1.3.Оценка риска с помощью показателей вариации.
Пример№3. Если известно, что при вложении капитала в мероприятие А из 120 случаев прибыль 25 млн. тенге была получена в 48 случаях (вероятность 0,4), прибыль 20 млн. тенге была получена в 36 случаях (вероятность 0,3) и прибыль 30 млн. тенге была получена в 36 случаях (вероятность 0,3), то среднее ожидаемое значение составит 25 млн. тенге (25*0,4+20*0,3+30*0,3).

---

Аналогично было получено среднее ожидаемое значение прибыли при вложении капитала в мероприятие Б – 30 млн. тенге = 40*0,3+30*0,5+15*0,2.

При сравнении вариантов А и Б можно прийти к выводу, что при вложении в мероприятие А величина прибыли колеблется в пределах от 20 до 30 млн. тенге, средний показатель прибыли – 25 млн. тенге; при вложении в мероприятие Б величина прибыли колеблется от 15 до 40 млн. тенге и средняя прибыль составляет – 30 млн. тенге (средняя арифметическая простая).

В данном случае по средней величине нельзя принять решение, необходимо оценить колеблемость величины прибыли по показателям вариации.

Колеблемость определяется как степень отклонения ожидаемого значения от средней величины. Для ее определения применяют показатели: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Дисперсия – это среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых:
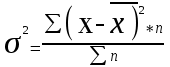, (5)

где 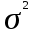- дисперсия;

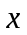- ожидаемое значение в каждом случае наблюдения;

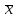- среднее ожидаемое значение;

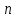- число случаев наблюдения (частота).
Среднее квадратическое отклонение определяется по формуле:
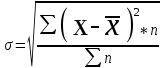, (6)

где 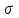- среднее квадратическое отклонение.
Если частоты появления событий равны, то в частном случае формулы будут записаны следующим образом:

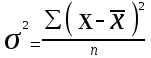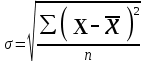, . (7, 8)

Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости и указываются в тех же единицах что и вариирующий признак.

Коэффициент вариации – это мера относительной колеблемости вариирующего признака, которая представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений.
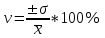, (9)

где v – коэффициент вариации, %;

---

- среднее квадратическое отклонение;

- среднее ожидаемое значение.
Коэффициент может изменяться от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Качественная оценка различных значений коэффициента вариации:

• 
  до 10% - слабая колеблемость;
  
• 
  10-25% - умеренная колеблемость;
  
• 
  свыше 25% - высокая колеблемость.
  

Расчет дисперсии при вложении капитала в мероприятия А и Б приведен в таблице1

Абсолютное значение вариации прибыли по мероприятию А

.

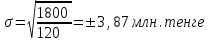Абсолютное значение вариации прибыли по мероприятию Б

.

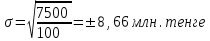Относительная вариация прибыли по мероприятию А

.

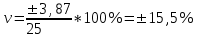Относительная вариация прибыли по мероприятию Б


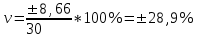
Таблица 1 – Расчет дисперсии

Номер события	Полученная прибыль, млн. тенге	Число случаев наблюдения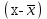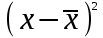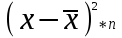
Мероприятие А
1	25	48	-	-	-
2	20	36	-5	25	900
3	30	36	+5	25	900
Итого	= 25	120			1800
Мероприятие Б
1	40	30	+10	100	3000
2	30	50	-	-	-
3	15	20	-15	225	4500
Итого	= 30	100			7500

---

Вариация возможной прибыли при вложении капитала в мероприятие А меньше, чем при вложении капитала в мероприятие Б. Таким образом решение принимается в пользу мероприятия А.
Пример№4. Условие предыдущего примера. Степень риска можно определять по упрощенной схеме. Риск инвестора характеризуется его оценкой вероятной величины максимального и минимального доходов. Чем больше диапазон между этими величинами при равной их вероятности, тем выше степень риска.

Для расчета вариации можно использовать формулы:
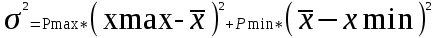; (10)

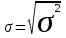; (11)

, (12)

где Pmax – вероятность получения максимального дохода (прибыли, рентабельности);

xmax – максимальная величина дохода (прибыли, рентабельности);

Pmin – вероятность получения минимального дохода (прибыли, рентабельности);

Xmin – минимальная величина дохода (прибыли, рентабельности).
При вложении капитала в мероприятие А имеем следующие значения этих показателей:

;

;


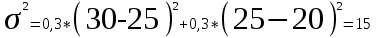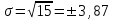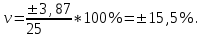
При вложении капитала в мероприятие Б имеем следующие значения этих показателей:







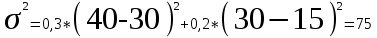
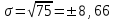
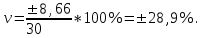
Сравнение мероприятий по показателям вариации показывает, что меньшая степень риска присуща вложению капитала в мероприятие А.
1.1.4 Оценка риска по прямым инвестициям с помощью коэффициента риска.
Пример№5. Соотношение максимально возможного объема убытка и объема собственных финансовых ресурсов инвестора представляет собой степень риска ведущего к банкротству. Она измеряется с помощью коэффициента риска:
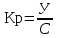; (13)

где Кр – коэффициент риска;

У - максимально возможная сумма убытка;

С – объем собственных финансовых ресурсов с учетом точно известных поступлений средств.
Таблица 2 – Выбор оптимального варианта вложения капитала по коэффициенту риска

---

Смотрите также файлы

• .docx

• Материалы и изделия на основе минеральных вяжущих веществ.doc

• Семинар 5 Литература.docx

• Требуется Для многопролетной балки сделать кинематический анализ и вывод о ее кинематических и статических признаках.docx

• Проблемы исторического познания. Формационный и цивилизационный подходы к истории, их сущность и познавательный потенциал.docx