ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 48
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Преподаватель: Портнягина Т.С., группа СТ-19-09, 1 курс.
Предмет: Математика
Дата: 26.02.2020
Тема урока: «Применение производной к исследованию функций»
Тип урока: Урок обобщения и систематизации знаний.
Цель урока: Деятельностная: формирование у учащихся способностей к обобщению и систематизации изучаемого предметного содержания. Образовательная: систематизация учебного материала.
Задачи урока:
-
систематизировать информацию и обобщать ее, работать в группах -
подвести обучающихся к пониманию того, что знание понятия производной необходимо человечеству в их жизни; -
совершенствовать умения ясно, логично и точно излагать свою точку зрения; -
обучать объективной оценке своих возможностей и успехов; -
способствовать развитию навыков устной речи, умению грамотно вести диалог и аргументировать свои действия; -
осознание большой практической значимости производной в жизни человека.
Оборудование урока: Проектор. Презентация. Карточки.
Формы работы с учащимися: Фронтальная. Индивидуальная. Групповая.
Методы обучения:
-
словесные: беседа; -
наглядные: компьютерная мультимедийная презентация; -
интерактивные: интерактивный диалог; -
практические: исследовательский, поисковый, организация применения знания производной при решении задач; -
методы контроля и самоконтроля: устный контроль, самоконтроль, взаимоконтроль.
Планируемые результаты:
-
осмысление роли производной в жизни человека -
выполнять логические операции, самостоятельно выделять и формулировать познавательную цель задания; -
структурирование знаний;
-
формирование речевой деятельности, навыков сотрудничества, умение находить общее решение, умение аргументировать своё предложение, взаимоконтроль и взаимопомощь по ходу выполнения задания.
Основные понятия, формируемые в процессе урока: область определения и область значений функции, промежутки знакопостоянства, производная, промежутки монотонности, экстремумы функции.
Структура и регламент урока
| Содержание этапов урока | Формируемые УУД | | |
| Деятельность преподавателя | Деятельность учащихся | Регламент (мин.) | |
Цель: Подготовить учащихся к работе на уроке, определить цели и задачи урока. | 2 | ||
| Приветствует детей, отмечает присутствующих, проверяет подготовленность к уроку, организует внимание учащихся. | Включаются в деловой ритм урока. | Личностные: самоорганизация Регулятивные: планирование своих действий в соответствии с требованиями Коммуникативные: использование в общении правил вежливости | |
Цель: Погружение в тему занятия, актуализация опорных знаний, создание условий для дальнейшей деятельности | 8 | ||
| Организует деловое общение, способствующее актуализации опорных знаний, дает задание на самостоятельное выполнение:
|
| Познавательные: умение понимать и реагировать на информацию в словесной форме Личностные: совершенствование имеющихся знаний и умений; Регулятивные: Коммуникативные: принимать активное участие в работе парами, умение вступать в диалог с преподавателем, участвовать в общей беседе, соблюдая правила речевого этикета, слушать и отвечать на вопросы других | |
| 3. Мотивация учебной деятельности Цель: мотивированное пробуждение интереса к теме. | 5 | ||
| Создает деловую атмосферу, позитивный настрой на активную деятельность и мыслительную работу. Настраивает обучающихся на продуктивную деятельность | Настраиваются на продуктивную мыслительную деятельность. | Личностные: выработка учебной мотивации; установления связи между целью учебной деятельности и ее мотивом; Коммуникативные: умение и готовность работать в коллективе. | |
Цель: Обобщить и систематизировать знания и навыки учащихся по теме “Применение производной к исследованию функций”. | 25 | ||
| Предлагает вспомнить алгоритм исследования функций с помощью производной. На доске прикрепляет листочки с этапами алгоритма и предлагает учащимся упорядочить их. Далее обучающимся предлагается исследовать функцию. Контролирует выполнение задания, советует при возникновении затруднений у учащихся. | Повторяют алгоритм исследования функции и построения ее графика и закрепляют навыки исследования функции с помощью производной в процессе решения задания. Выполняют в тетрадях задания самостоятельной работы по вариантам (по окончании выполнения обучающиеся защищают свою работу). | Познавательные: поиск и выделение необходимой информации, построение логической цепи рассуждения, формирование интереса к данной теме Личностные: осознание ответственности за общее дело Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата Коммуникативные: выражение своих мыслей с достаточной полнотой и точностью, слежение за действиями других участников в процессе коллективной деятельности | |
Цель этапа. Проанализировать, дать оценку успешности достижения цели и наметить перспективу на будущее. | 3 | ||
| Учитель выставляет баллы за урок, инициирует рефлексию учащихся их собственной учебной деятельности на уроке. | Высказывают свое мнение по поводу собственной учебной деятельности на уроке, осуществляют взаимооценку. | Познавательные: осознанное и произвольное построение речевого высказывания, Личностные: Регулятивные: Коммуникативные: | |
План-конспект урока
-
Организационный этап.
(Урок по теме «Применение производной к исследованию функций» проводится после изучения геометрического и физического смысла производной, правил дифференцирования, производных элементарных функций. Форма организации учебной деятельности как групповая, так и индивидуальная).
Преподаватель: Здравствуйте, ребята, садитесь. У нас сегодня на уроке присутствуют гости, давайте с ними поздороваемся.
Преподаватель отмечает отсутствующих, проверяет готовность студентов к уроку.
Преподаватель: Ребята, если вы правильно отгадаете ключевое слово, то узнаете тему нашего урока;
1) С ее появлением математика перешагнула из алгебры в математический анализ;
2) имеет геометрический и механический (физический) смысл;
3) Бывает первой, второй, … ;
4) Обозначается штрихом.
Учащиеся отгадывают ключевое слово («производная») и записывают тему урока.
Преподаватель: Итак, тема нашего занятия “Применение производной к исследованию функций»”.
На этом уроке мы повторим и закрепим исследование функции с помощью производной.
-
Актуализация опорных знаний.
-
Преподаватель предлагает составить цветок понятий (ассоциативный куст): для этого студентам нужно назвать понятия, которые ассоциируются с темой «Производная». (1 балл за ответ)
Учащиеся в устной форме отвечают на вопрос, записывают себе в оценочный лист баллы за правильный ответы
2) Задание «Найди соответствие»:
| А | Б | В | Г | Д | Е | Ж |
| | | | | | | |
| № | Функция f(x) | | Производная  |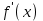
| А. | C (постоянная) | 1 |  |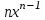
| Б. | 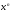 | 2 | 0 |
| В. | kх+b | 3 | k |
| Г. | sin x | 4 |  |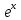
| Д. | cos x | 5 | - sin x |
| Е. | tg x | 6 | cos x |
| Ж. | 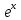| 7 |  |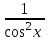
Ребята выполняют задание, после завершения которого проверяют друг у друга ответы (сверяясь с ответом на доске). Ставят по 1 баллу за каждое правильное соответствие. Правильный ответ 2 1 3 6 5 7 4.
-
Разбор заданий из открытого банка ЕГЭ (устно, на слайде):
-
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8).
Определите:
- количество промежутков монотонности,
- количество экстремумов на данном интервале
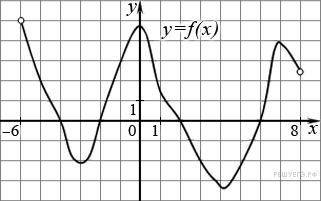Ответ: 5, 42. На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].
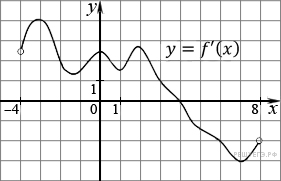Ответ: х=4За правильный ответ – 1балл
3. Мотивация учебной деятельности
С помощью производной учитывая её механический смысл и геометрический смысл, можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. Например, рассмотрим применение производной в задачах строительства
Задача:
О
пределить размер такого открытого бассейна с квадратным дном и объемом 32см³, чтобы на облицовку его стен и дна было истрачено наименьшее количество материала.
Решение:
Обозначим длину стороны квадрата x м,
а высоту бассейна y м. Тогда
м3.Площадь боковой поверхности бассейна с площадью дна равна
Найдем
м2, тогда
.Найдем производную этой функции:
; 
; 
Поскольку
при
, а 
при 
, то 
– точка минимума (наименьшего знания функции). Значит наименьшие размеры бассейна, заданного объема V=32м³ такие ; y=
м.Ответ: 2м; 4м и 4м
Как вы видите, производная нужна не только в математике, она является мощным инструментом для решения и физических, экономических, химических задач.
4. Этап обобщения и систематизации знаний и умений.
Преподаватель предлагает вспомнить алгоритм исследования функций с помощью производной, раздает листочки с этапами алгоритма и поручает учащимся упорядочить их. (учащиеся предварительно разбиваются на 2 группы), по окончании группы сверяются с правильной последовательностью этапов.
Далее обучающиеся исследуют функцию и строят её график (эскиз графика):
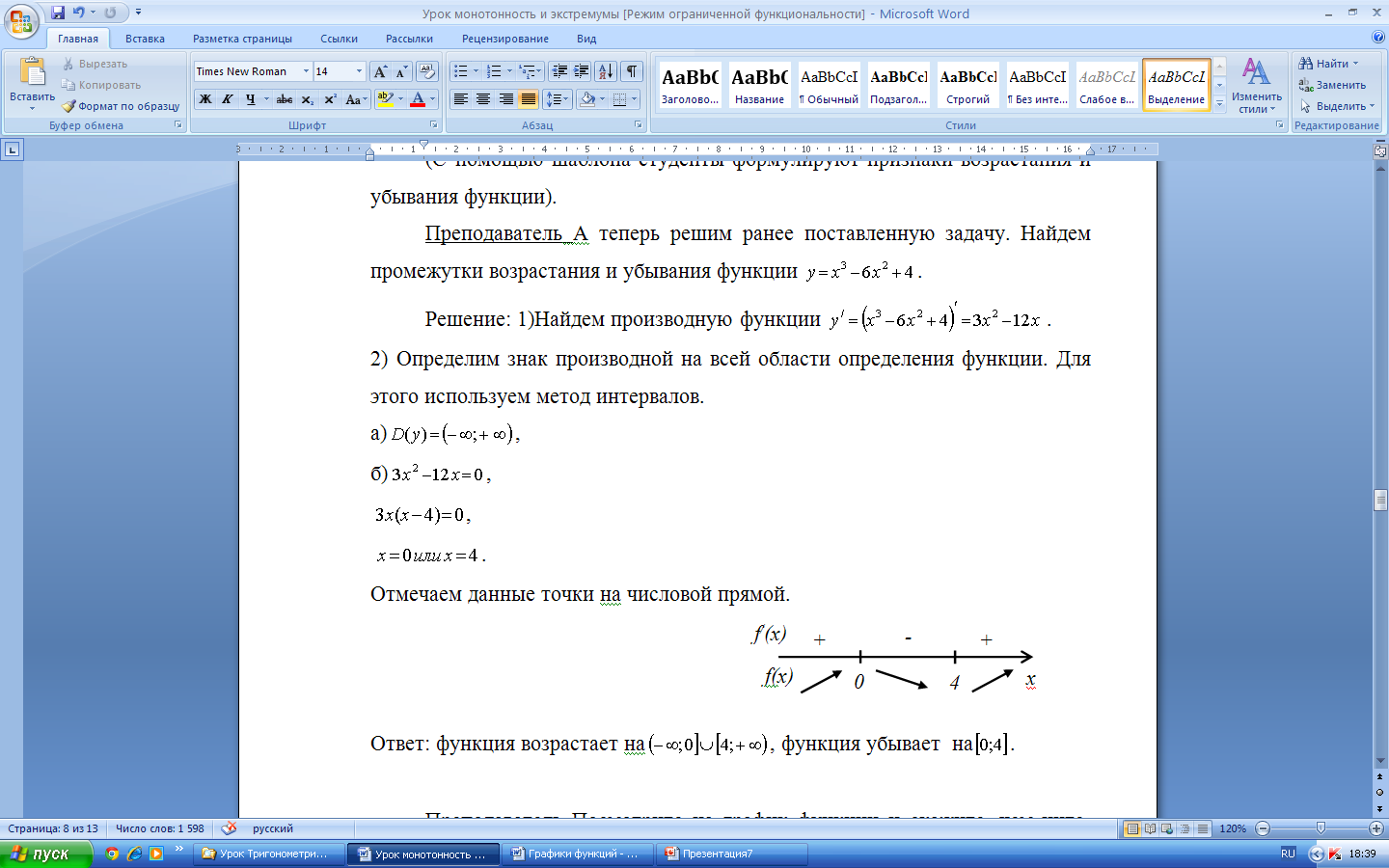
1 группа: у = х3 - 6х² + 4
2 группа: у = 2х3 + 3х2 – 1
D(y) = (-∞; +∞)
У’ = 6х2 + 6х
6х2 + 6х = 0
Функция возрастает на промежутках
и 
Функция убывает на промежутке
.Группы защищают свою работу, за каждое правильное утверждение ставится 1 балл.
5. Подведение итогов урока. Рефлексия.
Наш урок подходит к концу. Подведем итоги, просуммируйте все ваши баллы и предлагаю каждому окончить одну из фраз, которую вы видите на экране:
- сегодня на уроке…
- мне понравилось…
- было трудно…
- я научился…
- Сегодня я узнал…
-
Было интересно… -
Было трудно… -
Я выполнял задания… -
Теперь я могу… -
Я научился… -
Я смог… -
Мне захотелось…
Преподаватель ставит баллы, устно оценивает урок, деятельность учащихся, отмечает активных, инициативных студентов и благодарит за урок
Производная в физике.
Задача №1
Координата материальной точки изменяется с течением времени по закону s(t) = 3t 2 - 7t + 6. Найдите скорость точки в момент времени t = 6с.
Решение:
s(t) = 3t2 -7t + 6
Т.к. ???? (t) = s′(t), то ???? (t) = 6t-7.
???? (6) = 36 - 7= 29(м/с)
Ответ: 29 м/с.
Задача №2
Найдите силу F , действующую на материальную точку массой m , движущуюся прямолинейно по закону s(t) = 2t3 - t2 (м) при t = 2 с .
Решение:
Т.к. ????(t) = s′(t), то ????(t) = 6t2 - 2t.
Т.к. a(t) = ????′(t), то a(t) = 12t - 2,
a(2) = 24 - 2 = 22(м /c2)
Т.к. F = ma, то F = 22m(H).
Ответ: 22m H.
Производная в химии.
Как используют производную в химии?
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности.
Определение: скоростью химической реакции в химии называется изменение концентрации реагирующих веществ в единицу времени или производная от концентрации реагирующих веществ по времени.
Формула производной в химии: если P(t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость (t) химической реакции в момент времени t равна производной, т.е. (t) = P'(t) =.