ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 65
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определите:
- средний размер основных фондов предприятия;
- среднее квадратическое отклонение;
- среднюю ошибку выборки при определении среднего размера основных фондов;
- предельную ошибку выборки при значении доверительной вероятности 0,954;
- пределы, в которых находится средний размер основных фондов в генеральной совокупности предприятий.
-
Средний размер основных фондов:
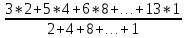 =8
=8-
Среднее квадратическое отклонение:
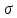 =
=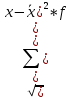 =
=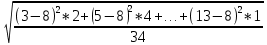 =2,635
=2,635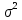 =2,635^2=6,941
=2,635^2=6,941-
Средняя ошибка выборки:
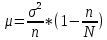 , n=34, выборка 5%
, n=34, выборка 5%N=
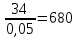
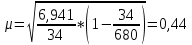
-
Предельная ошибка выборки при вероятности 0,954:
m=20
W=20/34=0,6
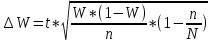 = 2*(
= 2*(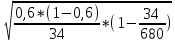 =0,16
=0,16-
(Интервал для генеральной совокупности:
0,6-0,16<=p<=0,6+0,16
0,44<=p<=0,76
44%<=p<=76%)
-
Предельная ошибка выборки при вероятности 0,997:
0,4*3=1,2
8-1,2 <= p <= 8+1,2
6,8 <= p <= 9,2
Вопрос 47 (10 баллов) В таблице представлены данные о грузообороте отдельных видов транспорта в процентах к грузообороту автомобильного транспорта. Определите удельный вес видов транспорта в общем грузообороте.
| Вид транспорта | Грузооборот, % |
| Автомобильный | 50 |
| Железнодорожный | 47 |
| Морской | 20 |
| Речной | 30 |
| Воздушный | 62 |
| Трубопроводный | 71 |
| Итого: | 280 |
Удельный вес:
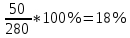 ;
;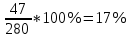 ;
; 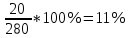 ;
;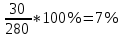 ;
;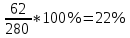 ;
;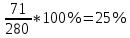 ;
;В сумме удельный вес = 100%
Вопрос 48 (10 баллов) Уровень преступности в регионе характеризуется коэффициентами роста по сравнению с предыдущим годом:
| | 2017 г. | 2018 г. | 2019 г. | 2020 г. | 2021 г. |
| Коэффициент роста | 1 | 0,95 | 0,97 | 0,96 | 0,92 |
Определите среднегодовое изменение уровня преступности за период с 2017 по 2021 гг.
Цепной темп прироста:
(Делим больший год на меньший и так для каждого года)
| 1 | 0,95 | 1,021 | 0,94 | 0,979 |
Среднегодовое изменение уровня преступности:
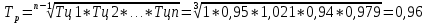
Вопрос 49 (20 баллов) Известны следующие данные по двум филиалам организации:
| Филиал | Отработано, человеко-часов | Средняя часовая выработка продукции, руб. | |||
| базисный период | отчетный период | базисный период | отчетный период | ||
| 1 | | | | | |
| 2 | | | | | |
Определите:
-
индивидуальные индексы объема производства; -
сводный индекс объема производства; -
сводный индекс производительности труда; -
прирост продукции за счет повышения производительности труда в целом по организации.
индивидуальные индексы физического объема
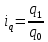
Товар А:
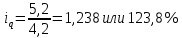
Товар Б:
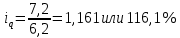
индекс производительности труда Iw=
Вопрос 50 (10 баллов) Имеются следующие данные:
| Вид Продукции | Общая сумма затрат на производство продукции, тыс. руб. | Изменение себестоимости единицы продукции в отчетном периоде по сравнению с базисным, % | |
| Базисный период | Отчетный период | ||
| А В С | | | |
Определите общий индекс себестоимости.
Вопрос 51 (10 баллов) Имеются следующие данные об активах коммерческого банка в одном из регионов за 2019 г. на первое число каждого месяца, млн руб.:
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
| 189 | 190 | 205 | 226 | 208 | 195 | 190 |
Определите:
- среднюю величину активов банка за 1 квартал, 2 квартал и 1 полугодие 2019 г.
- среднемесячные темпы роста активов в 1 квартале и 2 квартале 2019 г.
Средняя величина активов:
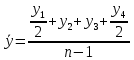
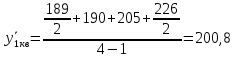
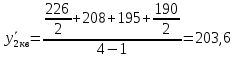
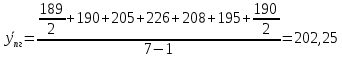
Среднемесячные темпы роста:
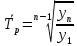
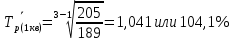
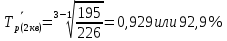
Вопрос 52 (20 баллов) Имеются следующая выписка из платежной ведомости:
| Ф.И.О. | Заработная плата, тыс. руб. | Ф.И.О. | Заработная плата, тыс. руб. |
| Иванов | 87000 | Порошенко | 120000 |
| Петров | 55000 | Путин | 350000 |
| Сидоров | 67000 | Медведев | 150000 |
| Игнасенков | 83000 | Жириновская | 120000 |
Определите:
1) среднюю заработную плату;
2) среднее линейное отклонение;
3) среднее квадратическое отклонение;
4) относительные показатели вариации заработной платы (относительное линейное отклонение, коэффициент вариации).
-
Средняя заработная плата:
 =
= 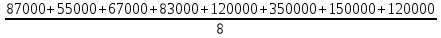 = 129000
= 129000-
Среднее линейное отклонение:
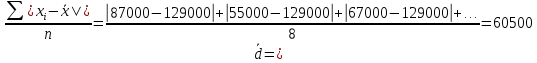
-
Среднее квадратическое отклонение
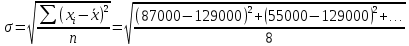 = 88490,11
= 88490,11-
Относительное линейное отклонение
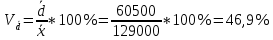
-
Коэффициент вариации:
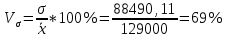
Вопрос 53 (20 баллов) В таблице представлены данные о сумме прибыли организаций отрасли за 9 лет, млрд руб.:
| Год | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| Сумма | 7 | 5 | 13 | 12 | 16 | 14 | 15 | 21 | 22 |
Проведите динамический анализ прибыли организаций за 9 лет, Сделайте прогноз суммы прибыли на 2018 г. на основе:
- среднегодового абсолютного прироста;
- среднегодового темпа роста;
- аналитического выравнивания ряда динамики.
-
Среднегодовой абсолютный прирост:
 =
= 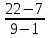 = 1,875
= 1,875-
Среднегодовой темп роста:
 =
= 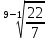 = 1,15
= 1,15-
Аналитическое выравнивание ряда динамики:
Проведем аналитическое выравнивание ряда динамики годовых объемов реализации продукции.
Линейное уравнение тренда имеет вид:
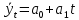
где t – порядковый номер периодов (или моментов) времени;
Условное обозначение времени удобно вводить так, чтобы сумма показателей времени ряда динамики была равна нулю:
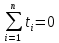
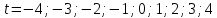
Тогда параметры уравнения тренда можно определить по формулам:
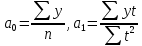
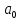 =
=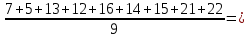 13,9
13,9| Расчет параметров уравнения тренда | |||||
| Год | Сумма прибыли организаций, млрд рублей (y) | Условное обозначение времени (t) | ty | t2 | Выравненные уровни ряда динамики, млрд рублей y̅t = 13,9+1,9*t |
| А | 1 | 2 | 3 | 4 | 5 |
| 1 | 7 | -4 | -28 | 16 | 6,29 |
| 2 | 5 | -3 | -15 | 9 | 8,19 |
| 3 | 13 | -2 | -26 | 4 | 10,09 |
| 4 | 12 | -1 | -12 | 1 | 11,99 |
| 5 | 16 | 0 | 0 | 0 | 13,89 |
| 6 | 14 | 1 | 14 | 1 | 15,79 |
| 7 | 15 | 2 | 30 | 4 | 17,69 |
| 8 | 21 | 3 | 63 | 9 | 19,59 |
| 9 | 22 | 4 | 88 | 16 | 21,49 |
| Итого | 125 | - | 114 | 60 | 125 |

