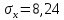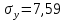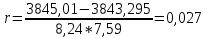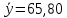Вопрос 1 (20 баллов) В таблице приведены данные о средних курсах доллара и курсе евро по месяцам 2017 г. Рассчитайте парный (линейный) коэффициент корреляции и сделайте вывод о характере взаимосвязи между курсами валют.

Месяц	Средний курс евро, руб.	Средний курс доллара, руб.
Январь	63,67	59,96
Февраль	62,18	58,4
Март	62,05	58,11
Апрель	60,42	56,43
Май	63,1	57,17
Июнь	64,84	57,83
Июль	68,64	59,67
Август	70,4	59,65
Сентябрь	68,8	57,7
Октябрь	67,87	57,73
Ноябрь	69,11	58,92
Декабрь	69,36	58,59

1. 
   Парный (линейный) коэффициент корреляции:
   

2. 
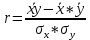
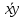   = 3845,01 (среднее произведение)
   
3. 
   
   

4. 
   
   

5. 
   
   
6. 
   
   

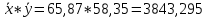
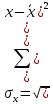
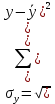
Сформулируем вывод: между рассматриваемыми показателями существует слабая прямая линейная связь, т.к. коэффициент корреляции находится в промежутке от 0 до 0,25.

Вопрос 2 (20 баллов) Динамика пассажирооборота авиакомпании характеризуется показателями:

---

Известно, что пассажирооборот в 2020 г. увеличился на 17 млн пассажиро-км. Определите пассажирооборот в 2016 и 2020 гг., среднегодовой абсолютный прирост и темп роста пассажирооборота за рассматриваемый период.

Год	2016	2017	2018	2019	2020
Значения	x	1,05*x	1,03*1,05*x	1,02*1,03*1,05*x	1,06*1,02*1,03*1,05*x

Зная, что в 2020 году пассажирооборот увеличился на 17 млн по сравнению с 2019, получаем:
1,02*1,03*1,05*x + 17 = 1,06*1,02*1,03*1,05*x

1,10313*x + 17 = 1,1693178*x

x = 256,84
Пассажирооборот в 2016 году = 257 млн пассажиро-км

Пассажирооборот в 2020 году = 1,06*1,02*1,03*1,05*256,84 = 300 млн пассажиро-км
Среднегодовой абсолютный прирост:

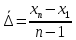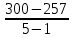= = 10,75
Среднегодовой темп роста:

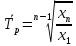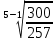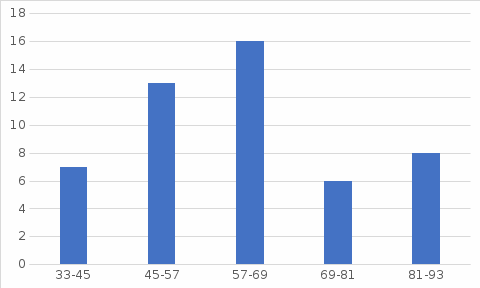
= = 1,04

Вопрос 3 (10 баллов) Суммы страховых выплат по ОСАГО (тыс. руб.) приведены в таблице. Постройте интервальный ряд распределения и изобразите его графически.

36	38	36	57	55	50	36	60	60	40
91	75	88	46	66	64	72	47	46	54
55	40	45	69	85	83	47	51	83	59
46	67	62	72	79	33	62	86	46	73
66	68	93	82	56	65	61	59	66	65

---

Интервальный ряд	Количество
33-45	7
45-57	13
57-69	16
69-81	6
81-93	8
Итого	50

Вопрос 4 (10 баллов) Имеются данные по трем филиалам организации:



Определите по организации в целом средний процент изменения объема продукции в отчетном периоде, средний удельный вес экспортной продукции в отчетном периоде.
Средний процент изменения объема продукции в отчетном периоде:

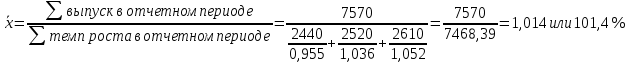
Средний процент прироста равен +1,4%
Средний удельный вес экспортной продукции в отчетном периоде:


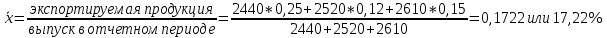
Вопрос 5 (20 баллов) В таблице приведены данные о среднем курсе евро по месяцам 2017 г. Проведите сглаживание ряда динамики методом скользящей средней. Рассчитайте по сглаженному ряду

---

индексы сезонности.

Месяц	Средний курс евро, руб.	Скользящая трехчленная сумма	Скользящая средняя	Индекс сезонности
Январь	63,67	-	-	-
Февраль	62,18	187,9	62,63	95,19
Март	62,05	184,65	61,55	93,54
Апрель	60,42	185,57	61,86	94,01
Май	63,1	188,36	62,79	95,42
Июнь	64,84	196,58	65,53	99,59
Июль	68,64	203,88	67,96	103,28
Август	70,4	207,84	69,28	105,29
Сентябрь	68,8	207,07	69,02	104,90
Октябрь	67,87	205,78	68,59	104,25
Ноябрь	69,11	206,34	68,78	104,53
Декабрь	69,36	-	-	-

---

1. 
   Для второго столбика делаем сумму трёх членов слева, для первого и последнего месяца значений не будет
   
2. 
   Для третьего столбика берем значения из второго и делим на 3
   
3. 
   Индекс сезонности: ищем среднее для наших исходных данных (всё сложить и разделить на 12), потом берём наше первое значение – делим на среднее и умножаем на 100, так делаем для каждого значения
   

4. 
   
   

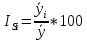
Вопрос 6 (20 баллов) Проведено 20 %-ное выборочное обследование страховых компаний, в результате которого по 100 отобранным компаниям получены данные:

- средний размер выплат по КАСКО – 5000 руб.

- среднее квадратическое отклонение 300 руб.

Определите среднюю ошибку выборки и возможные пределы средней выплаты при значениях вероятности: 0,683; 0,954; 0,997.

Средняя ошибка выборки для средней величины μ_x ̃ при механической выборке определяется по формуле:
где σ^2 –дисперсия выборочных значений признака.

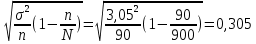руб.

Значение доверительной вероятности P(t)	0,683	0,954	0,997
Значение коэффициента доверия t	1,0	2,0	3,0

Определим предельную ошибку выборки при вероятности 0,954:
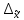= t * 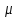= 2*0,305 = 0,61 руб.
Доверительный интервал для генеральной средней определяется неравенством:
????̃ − ????????̃ ≤ ????̅ ≤ ????̃ + ????????̃
Определим доверительный интервал для генеральной средней:
5000-0,61≤ x≤ 5000+0,61

4999,39≤ x≤ 5000,61

---

Смотрите также файлы

• 1тапсырма Дескриптор Координаталы жазытыта нктені координатасын табады Нктелеріні координаталарын жазады 1тапсырма.docx

• Экзаменационный билет 1 Приближенные числа, их абсолютные и относительные погрешности. Значимые и верные числа.docx

• Учебнопознавательные задачи как средство повышения учебной результативности на уроках математики.doc

• Математический диктант.docx

• Тема эссе Будущее без коррупции.docx