ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 29
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
излучаемая с поверхности
в единицу времени во всем интервале длин волн 
от 0 до 
и по всем направлениям полусферического пространства, т.е. в пределах телесного угла 
. 2. Поверхностная плотность потока излучения Е, Вт/м2. Это полный поток излучения с единицы поверхности тела,
, отсюда 
.3. Спектральная плотность потока излучения
, 
. Это плотность потока излучения в узком интервале длин волн, 
, отсюда 
или 
.4.Угловая плотность потока излучения
. Вначале удобнее пояснить эту величину, а потом дать ее определение. Рассмотрим единичную площадку (рис. 9.1). Проведем к ней нормаль n. Выберем некоторое произвольное направление под углом 
к нормали и в этом направлении выделим элементарный телесный угол 
. Обозначим поток излучения в пределах этого телесного угла в направлении через 
. Тогда угловой плотностью потока излучения называется плотность потока излучения в направлении к нормали в пределах элементарного телесного угла
, отнесенная к этому телесному углу, т.е.
. Аналогично спектральная угловая плотность потока излучения запишется 
.
Рис. 9.1 Рис. 9.2
5. Яркость или интенсивность излучения
. Это угловая плотность потока излучения, отнесенная к единице площадки, нормальной к направлению излучения. Проведем плоскость, нормальную к направлению излучения (рис. 9.1) и спроектируем единичную площадку на эту плоскость, очевидно, что величина этой проекции будет равна 
. Тогда согласно определению 
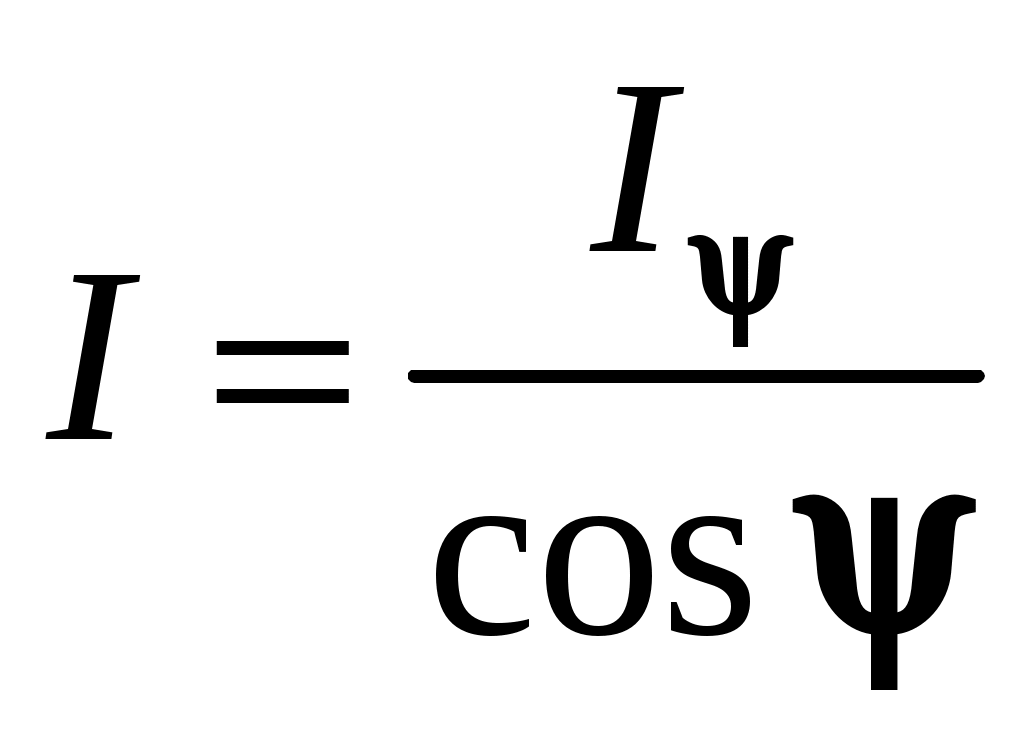. Аналогично можно получить, что спектральная яркость потока излучения будет равна 
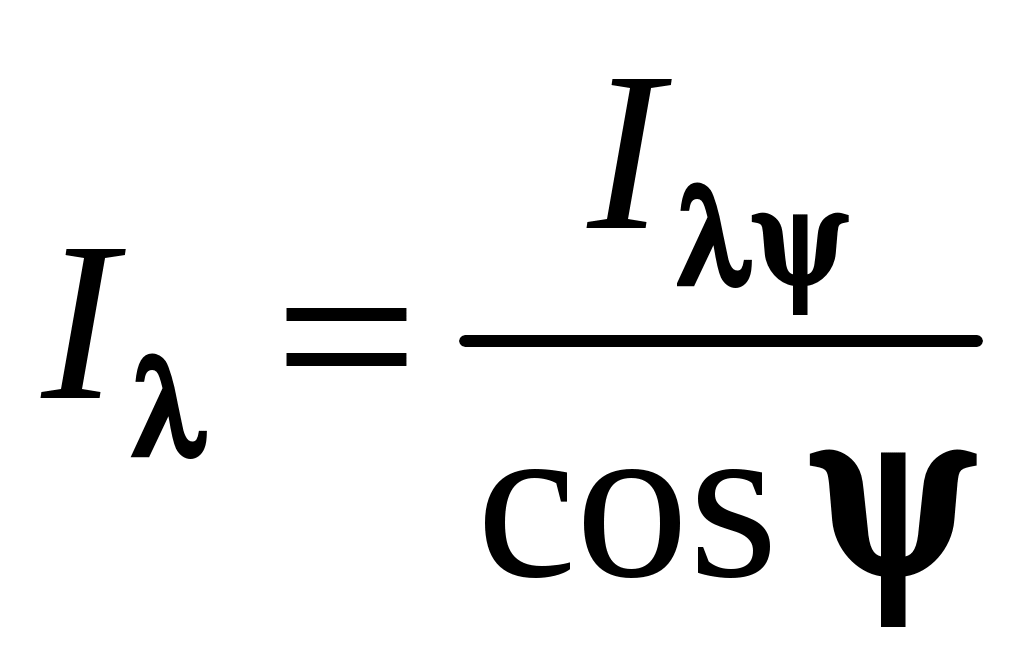.Используя определения угловой плотности и яркости потоков излучения, можно записать
. (9.1)Отсюда можно найти:
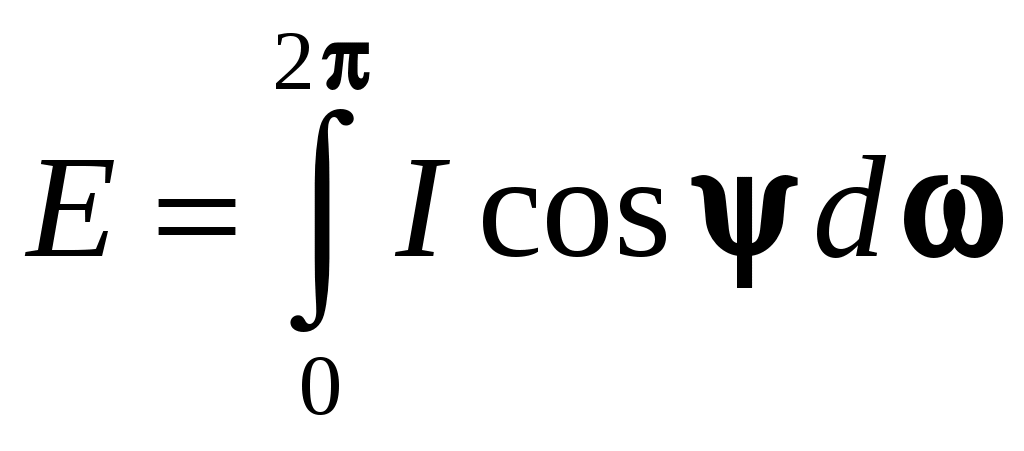. (9.2)9.1.2. Разновидности полусферического излучения
Различают следующие виды поверхностного излучения.
1. Собственное излучение. Его будем обозначать:
. Это излучение, которое определяется природой тела и его температурой.2. Падающее излучение. Его обозначают:
и т.д. Это излучение, которое падает на данное тело со стороны других тел. Пусть на поверхность некоторого тела падает излучение 
(можно работать с любой другой величиной). В общем случае (рис. 9.2) часть этого излучения отразиться (
), часть поглотиться (
), часть пройдет сквозь тело (
пропускательное). Тогда баланс энергии можно записать:
или, разделив на 
, получаем: 
.Здесь
коэффициент поглощения; 
коэффициент отражения; 
коэффициент проницаемости. С учетом сделанных обозначений 
. (9.3)Если А = 1, т.е. все лучи поглощаются, то такое тело называется абсолютно черным; если R = 1, т.е. все лучи отражаются, то такое тело называется абсолютно белым. Наконец, при D = 1 все лучи проходят сквозь тело, его называют прозрачным или диатермичным. Для поверхностного излучения
, поэтому 
(9.4)Для реальных тел
, и если к тому же коэффициент А не зависит от длины волны, то такое тело называется серым. Серое тело – это тоже абстракция, однако большинство реальных тел по своим свойствам приближается к серым.3. Эффективное излучение. Его обозначают
и т.д. Это сумма собственного и отраженного излучений, тогда, например,
. (9.5)4. Результирующее излучение. Его обозначают
и т.д. Это разность между излучением, которое посылает тело в пространство, а посылает оно эффективное излучение, и падающим на него со стороны других тел, отсюда, например, 
. (9.6)Используя (9.5), можно найти:
=
. Но для поверхностного излучения согласно (8.4) 
, поэтому 
, (9.7)другими словами, результирующее излучение равно также разности собственного и поглощенного излучений. Следует отметить, что результирующее излучение может быть положительным, отрицательным или равным нулю. Это необходимо учитывать при анализе процессов теплообмена излучением.
9.1.3. Соотношение, связывающее собственное, эффективное
и результирующее излучения
Выразим из уравнения (9.6)
, а падающее излучение – из (9.7): 
и подставим его в первое соотношение:
. (9.8)Это соотношение используется при решении многих задач по излучению, а сам способ называется методом сальдо. Кроме него существуют и другие методы, например, метод многократных отражений, зональный метод и др.
9.2. Основные законы теплового излучения
Строго говоря, все эти законы справедливы для абсолютно черного тела при равновесном излучении. Равновесным называется излучение, когда все тела, входящие в систему, имеют одинаковую температуру.
1. Закон Планка. Он устанавливает зависимость спектральной плотности потока излучения для абсолютно черного тела от длины волны и абсолютной температуры:
. В явном виде он записывается так:
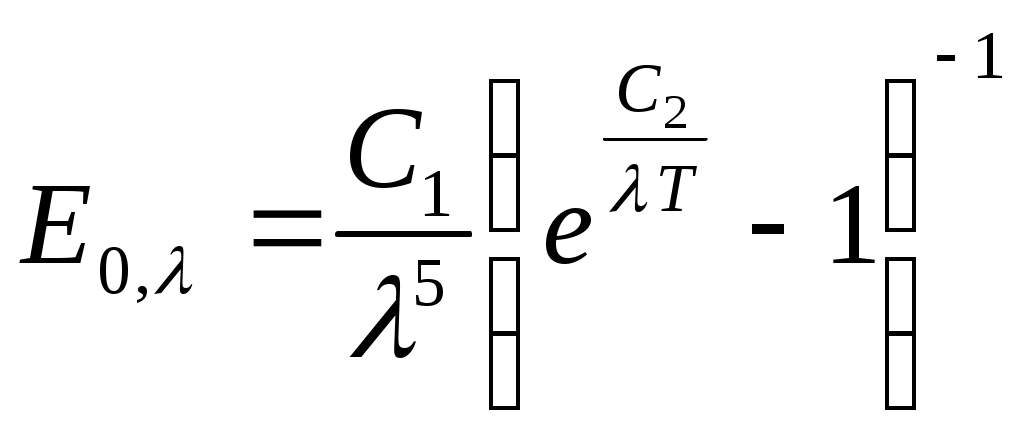, (9.9)где
и 
первая и вторая постоянные Планка. В теории тепломассообмена он рассматривается в качестве опытного закона или постулата. Изобразим уравнение (9.9) графически в виде зависимости
, а температуру будем брать в качестве параметра. Так как построенные таким образом кривые соответствуют
, то их будем называть изотермами. Итак, покажем несколько таких изотерм (рис. 9.3, а). На рисунке 
. Анализ приведенных кривых позволяет сделать следующие выводы.
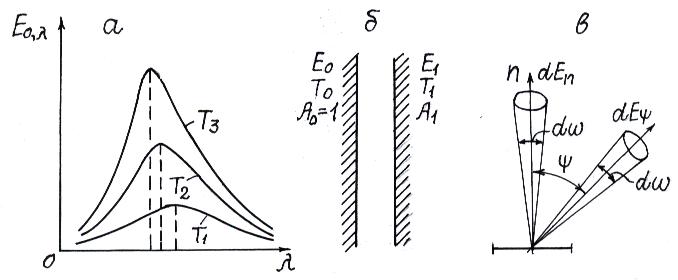
Рис. 9.3
1. Все кривые проходят через явно выраженный максимум.
2. При
или 
.3. С ростом температуры Т максимум кривых возрастает и смещается в сторону более коротких длин волн.
Последний вывод часто называют законом смещения Вина. Его можно получить из соотношения (9.8), проанализировав его на экстремум. Закон Вина записывается так:
, где 
.2. Закон Стéфана-Больцмана. Он устанавливает зависимость плотности потока излучения абсолютно черного тела от абсолютной температуры:
. Он был получен экспериментально Стефаном, теоретически обоснован Больцманом, а после установления закона Планка является его следствием. Действительно, из определения спектральной плотности потока излучения с учетом уравнения (9.8) можно найти, что
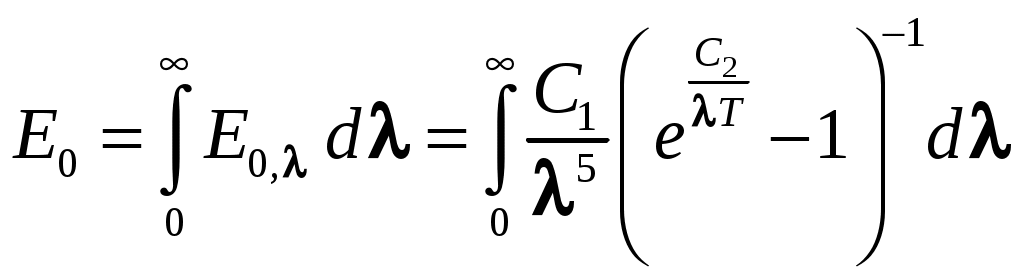, откуда после интегрирования 
, где 
. Формулировка закона: плотность потока излучения абсолютно черного тела пропорциональна абсолютной температуре в четвертой степени. В инженерной практике его обычно записывают так: 
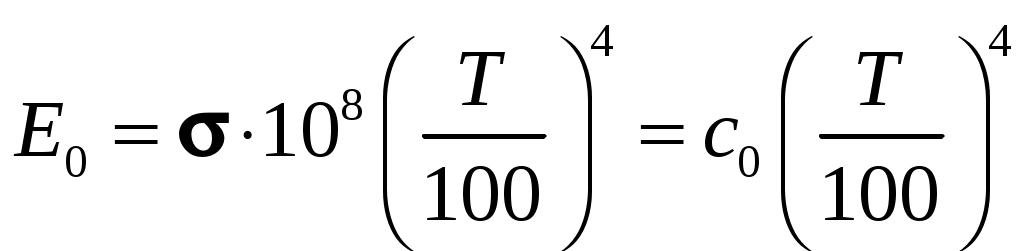, (9.10)где
называется коэффициентом излучения абсолютно черного тела. Это одна из мировых постоянных. Закон Стéфана-Больцмана распространяют и на серые тела. Известно, что при одинаковой температуре