ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 32
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
влияют на  в одинаковой степени справедливо лишь для углекислого газа. Для водяных паров влияние давления больше (см. уравнения (10.1)). Поэтому из номограммы можно найти лишь фиктивное значение
в одинаковой степени справедливо лишь для углекислого газа. Для водяных паров влияние давления больше (см. уравнения (10.1)). Поэтому из номограммы можно найти лишь фиктивное значение 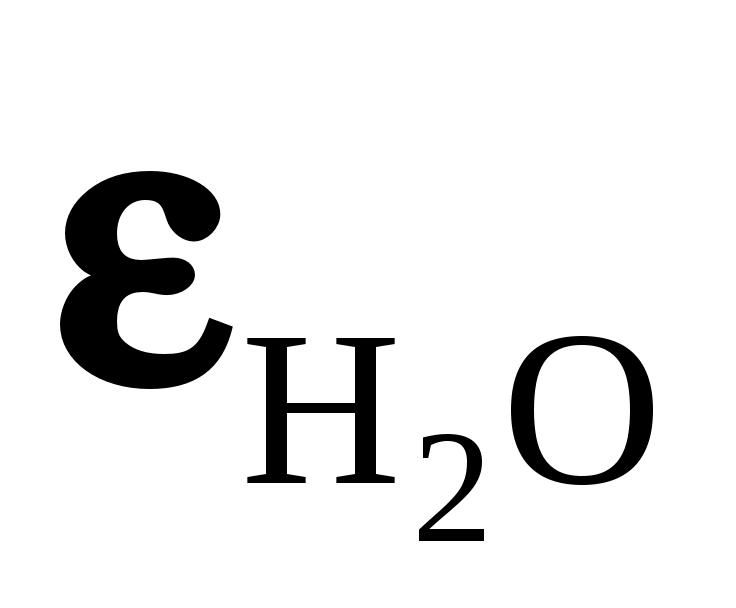 . Для получения истинной величины степени черноты водяных паров необходимо ввести поправочный множитель
. Для получения истинной величины степени черноты водяных паров необходимо ввести поправочный множитель 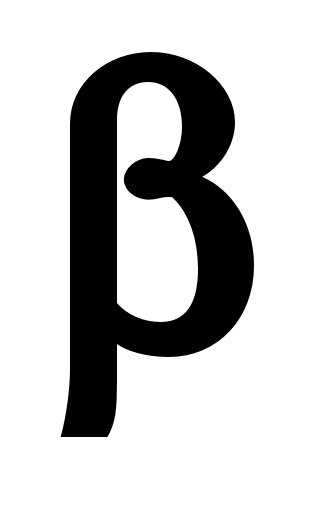 , зависящий от давления.
, зависящий от давления.
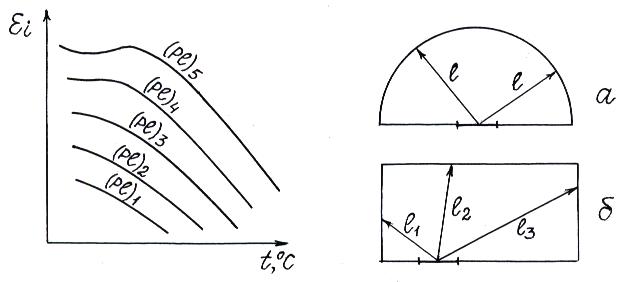
Рис. 10.1 Рис. 10.2
Ввиду того, что оба газа присутствуют в объеме одновременно, степень черноты смеси должна складываться из степеней черноты отдельных компонентов. Однако частично полосы излучения этих газов совпадают, в связи с чем итоговая степень черноты газового объема будет несколько меньше их суммы на величину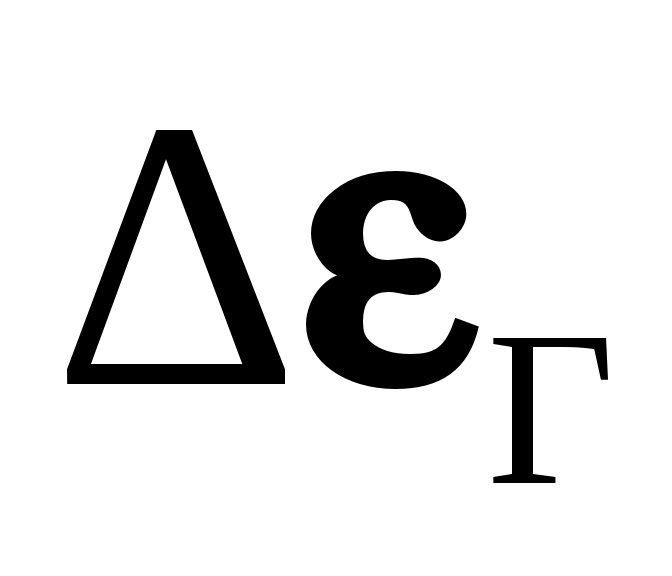 , поэтому окончательно
, поэтому окончательно
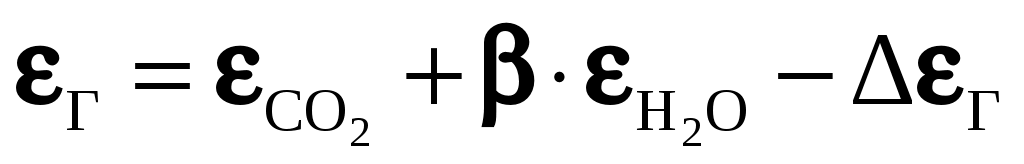 . (10.2)
. (10.2)
Зная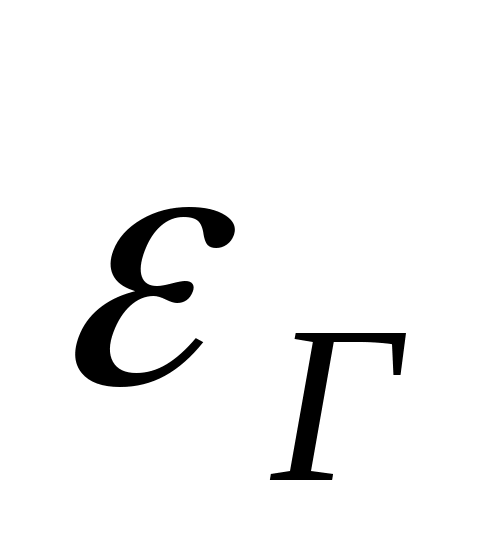 , собственное излучение газового объема на единицу поверхности ограждения найдется, как
, собственное излучение газового объема на единицу поверхности ограждения найдется, как 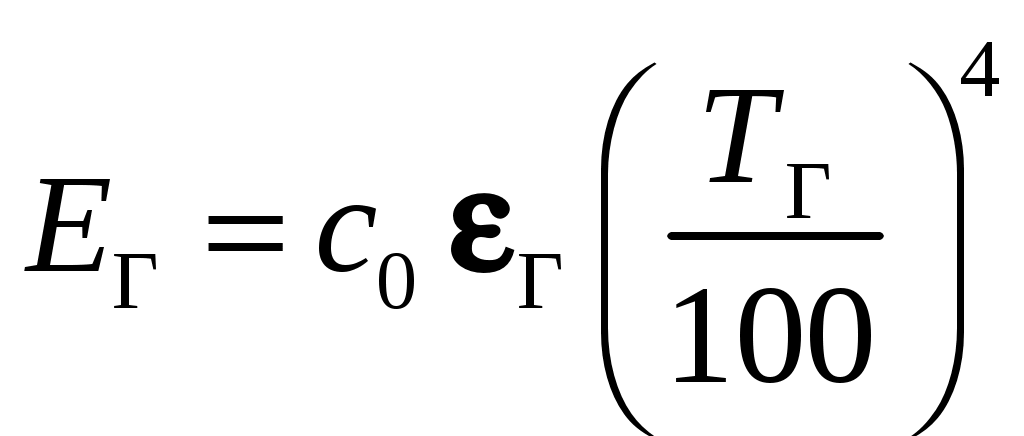 .
.
Но газовый объем огражден поверхностью, которая имеет свою температуру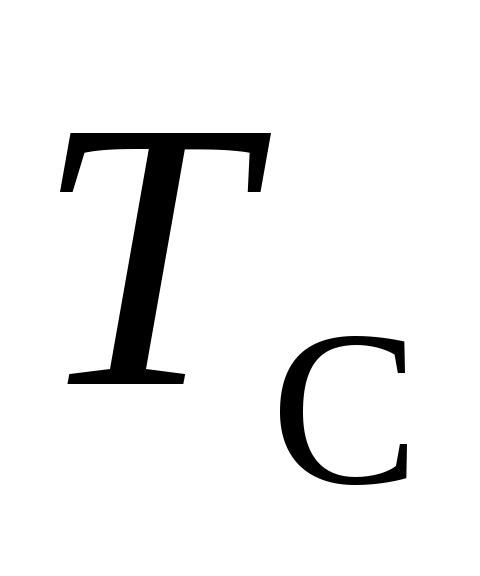 и степень черноты
и степень черноты 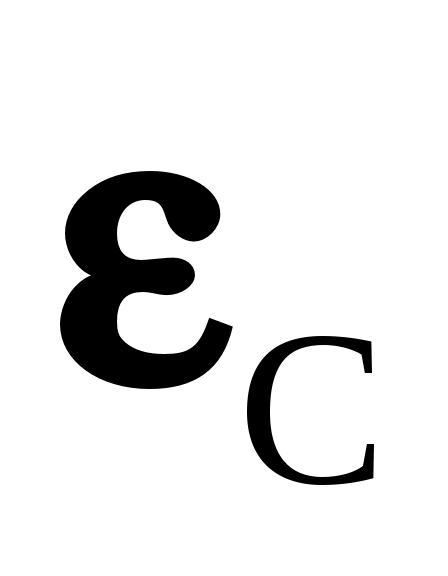 . Излучение этой поверхности частично поглощается газом, причем это излучение соответствует температуре ограждения. А так как
. Излучение этой поверхности частично поглощается газом, причем это излучение соответствует температуре ограждения. А так как 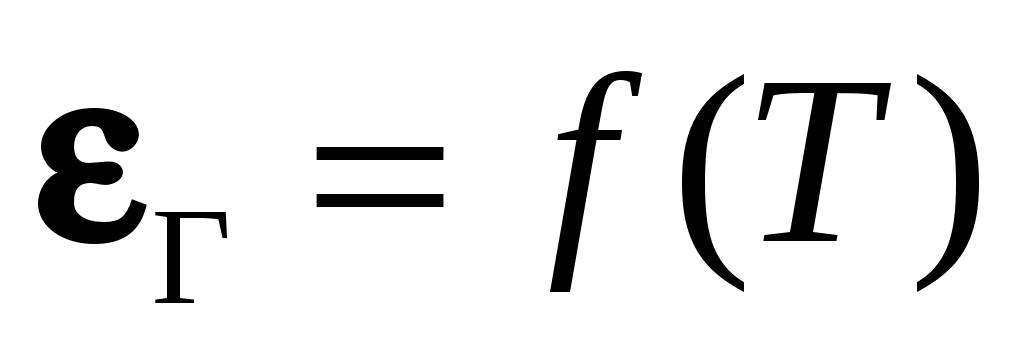 , то
, то 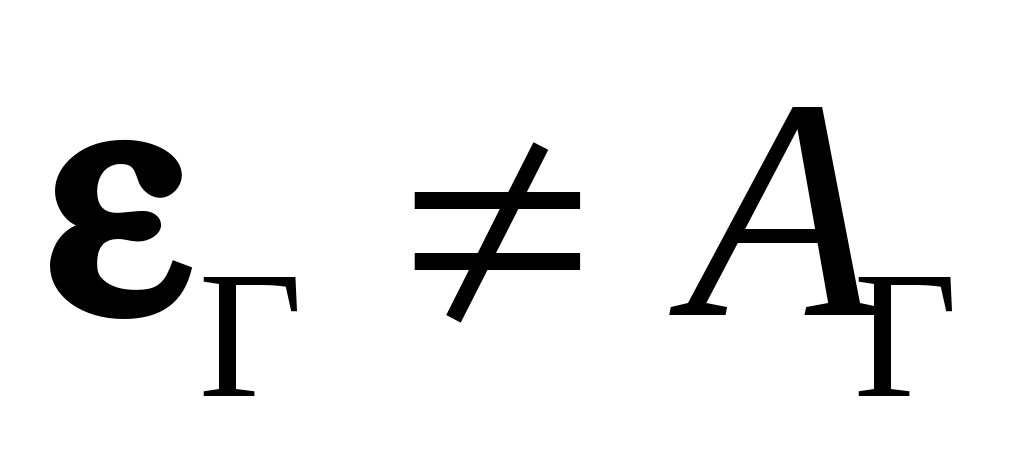 , где
, где 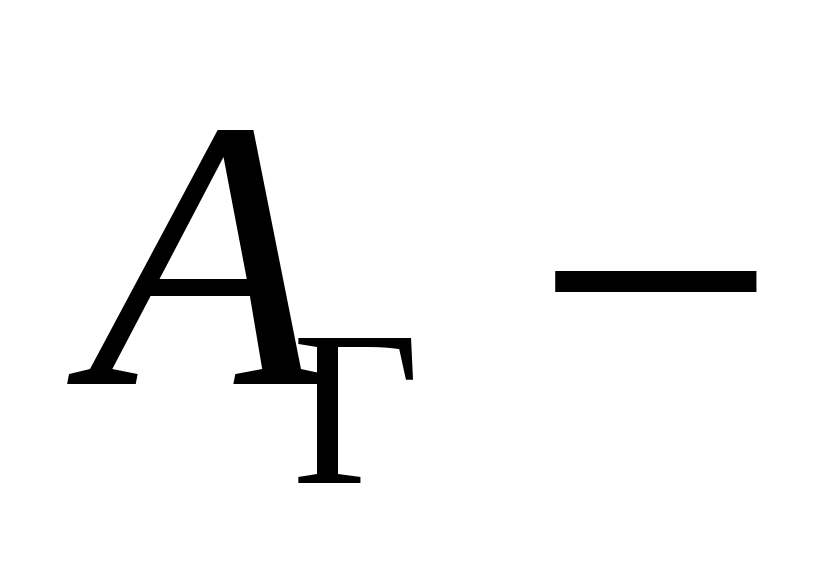 коэффициент поглощения газа. Результирующий поток будет равен разности между собственным и поглощенным излучениями. Кроме того, он пропорционален приведенной степени черноты стенки
коэффициент поглощения газа. Результирующий поток будет равен разности между собственным и поглощенным излучениями. Кроме того, он пропорционален приведенной степени черноты стенки 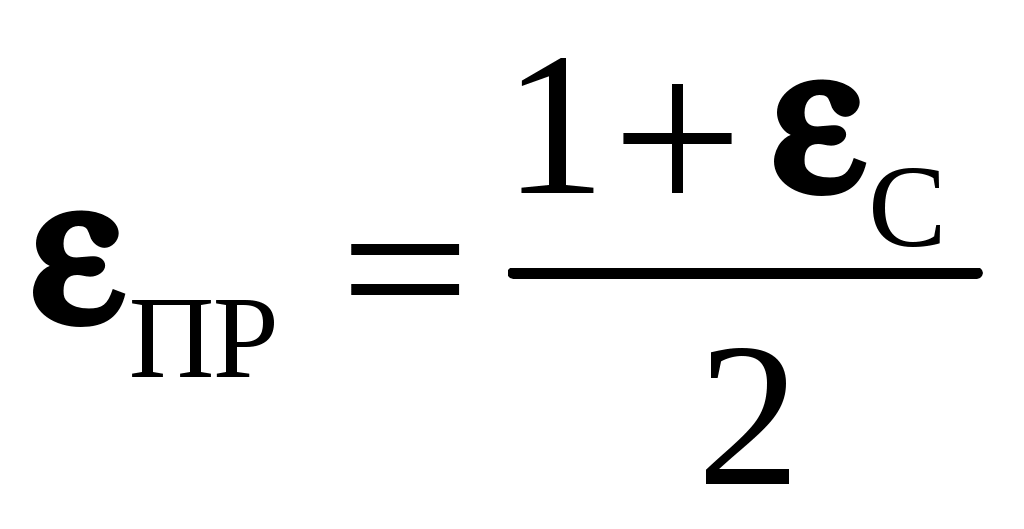 , если
, если 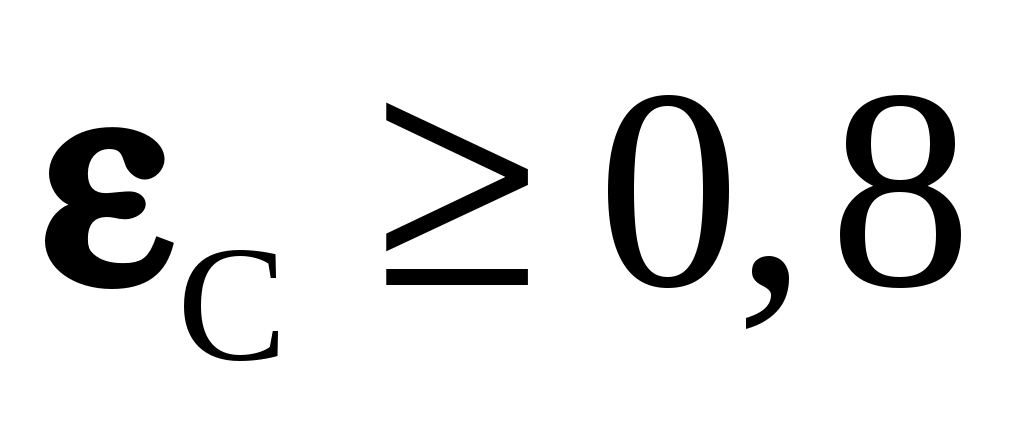
, поэтому
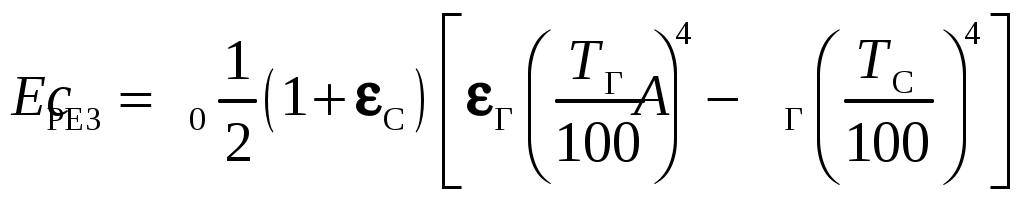 , (10.3)
, (10.3)
где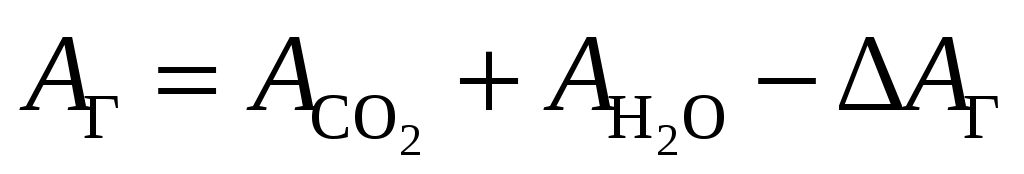 ;
; 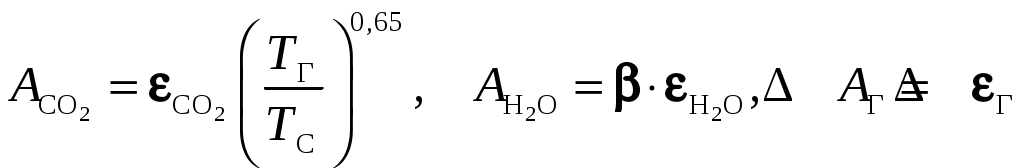 , причем
, причем 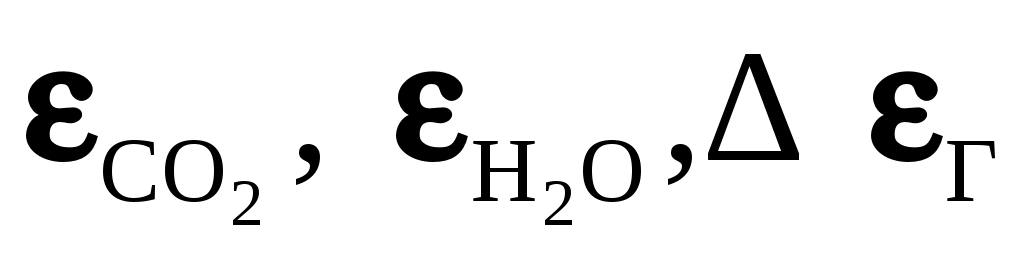 выбираются по тем же номограммам, только при температуре стенки
выбираются по тем же номограммам, только при температуре стенки 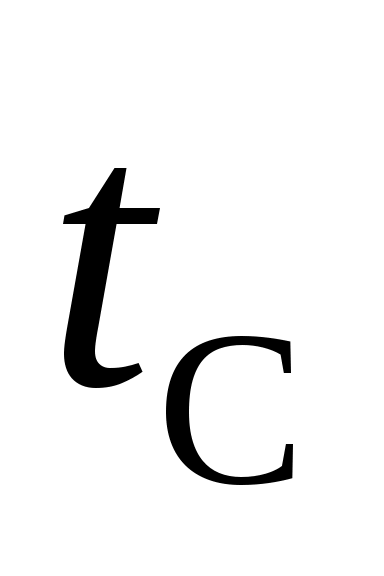 . Приведенная формула справедлива при теплообмене излучением между газовым объемом в виде полусферы и центральным элементом поверхности, расположенным в основании этой полусферы (рис. 10.3,а), т.е. когда длина луча
. Приведенная формула справедлива при теплообмене излучением между газовым объемом в виде полусферы и центральным элементом поверхности, расположенным в основании этой полусферы (рис. 10.3,а), т.е. когда длина луча  не зависит от направления. При излучении газовых объемов более сложной формы, например, шара, параллелепипеда (рис. 10.3,б) и др. величина
не зависит от направления. При излучении газовых объемов более сложной формы, например, шара, параллелепипеда (рис. 10.3,б) и др. величина  изменяется с направлением, поэтому расчет ведется для некоторой эквивалентной полусферы с радиусом
изменяется с направлением, поэтому расчет ведется для некоторой эквивалентной полусферы с радиусом 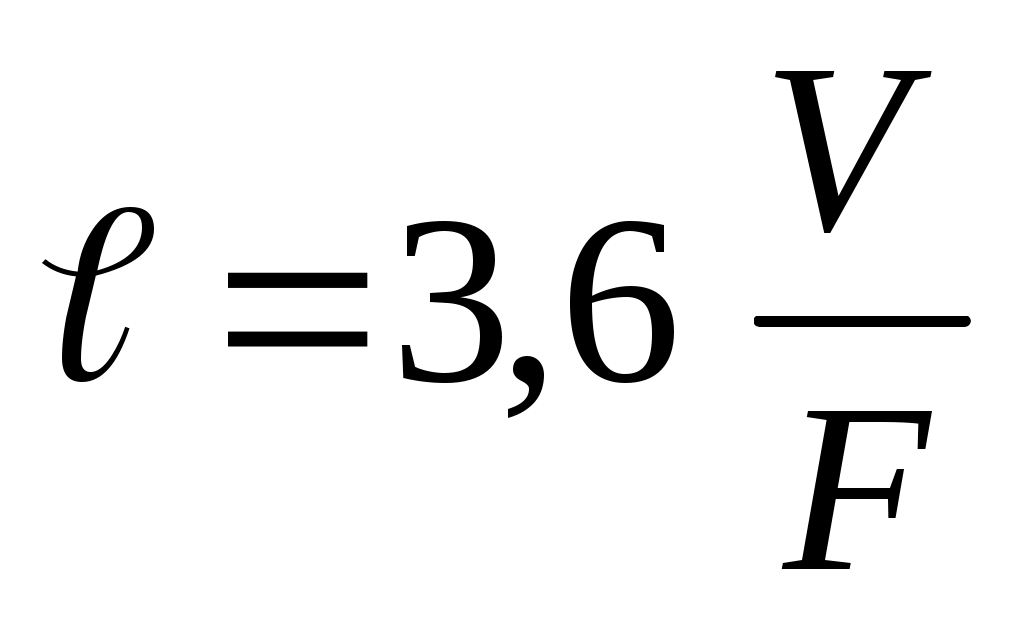 , где
, где 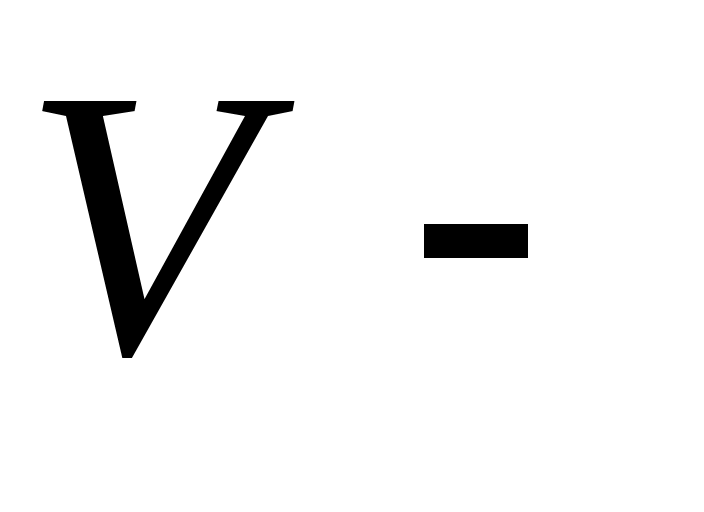 объем, занимаемый газом;
объем, занимаемый газом; 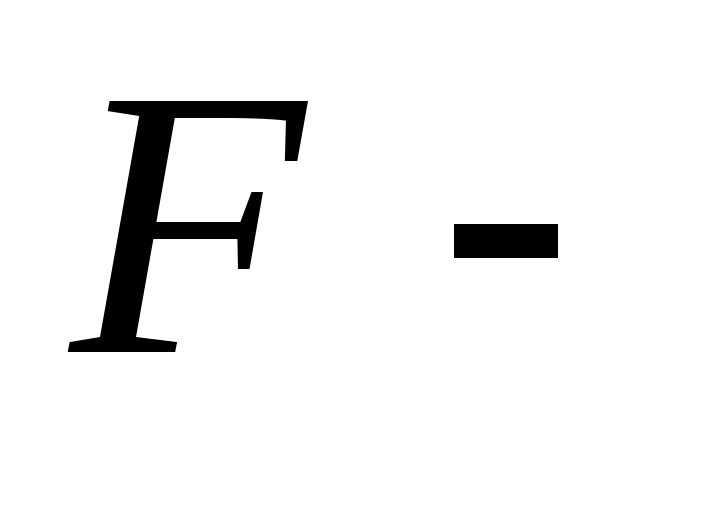 поверхность ограждения.
поверхность ограждения.
В более сложных случаях, например, при теплообмене излучением между газом и размещенным в нем пучком труб, расчет ведется по эмпирическим формулам, в частности,
ведется по эмпирическим формулам, в частности,
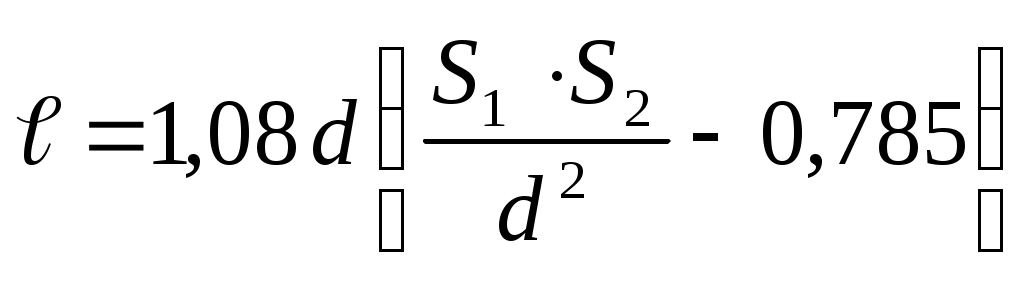 ,
,
где d – внешний диаметр труб пучка;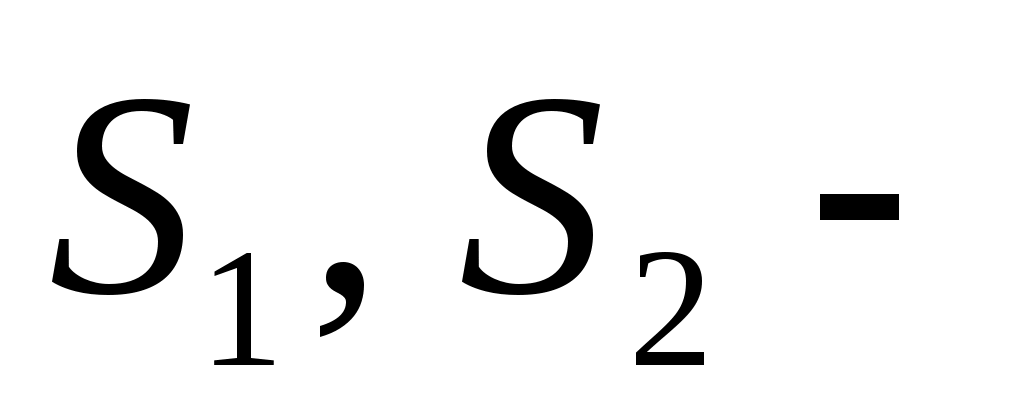 поперечный и продольный шаги пучка.
поперечный и продольный шаги пучка.
Приведенным методом расчета пользуются при сжигании природного или искусственного газов. При камерном сжигании твердого (в виде пыли) и жидкого топлив расчет ведется по методике, основанной на применении закона Бугера, записанного в форме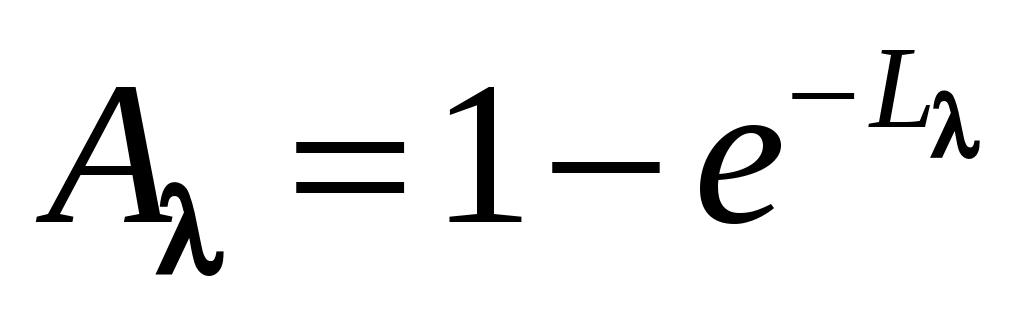 , где
, где  – коэффициент поглощения среды с учетом твердых включений;
– коэффициент поглощения среды с учетом твердых включений; 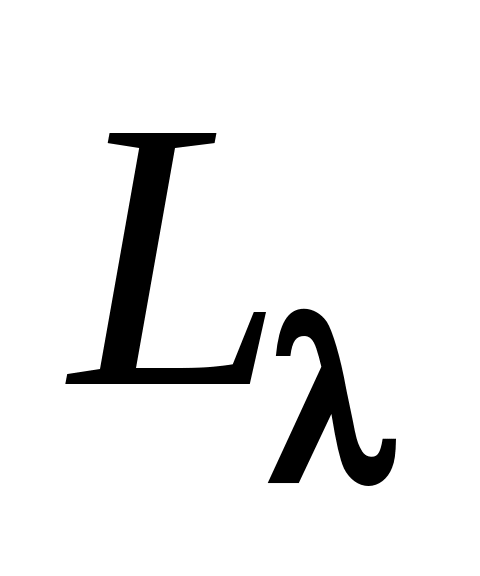
– оптическая толщина среды.
10.2. Расчет радиационно-конвективного теплообмена.
При размещении поверхности теплообмена в высокотемпературном потоке газа необходимо кроме конвекции учитывать и излучение. В этом случае применяется метод эквивалентного или эффективного коэффициента теплоотдачи, в котором в качестве основного принимают процесс конвективного теплообмена (теплоотдачи), характеризуемого коэффициентом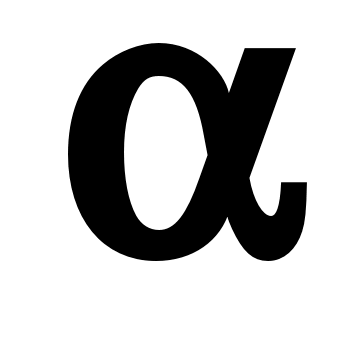 , а излучение учитывается поправкой
, а излучение учитывается поправкой  , тогда
, тогда 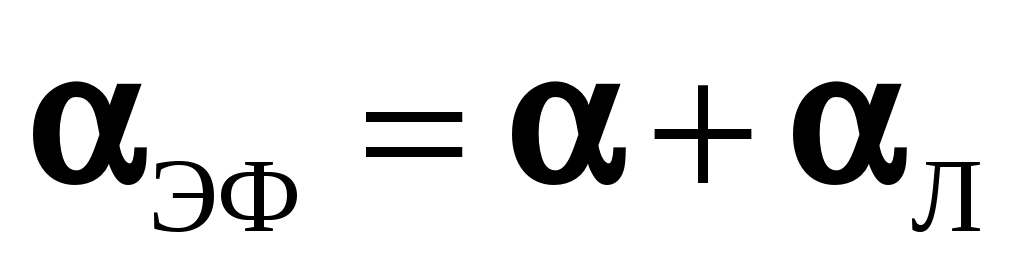 , где
, где 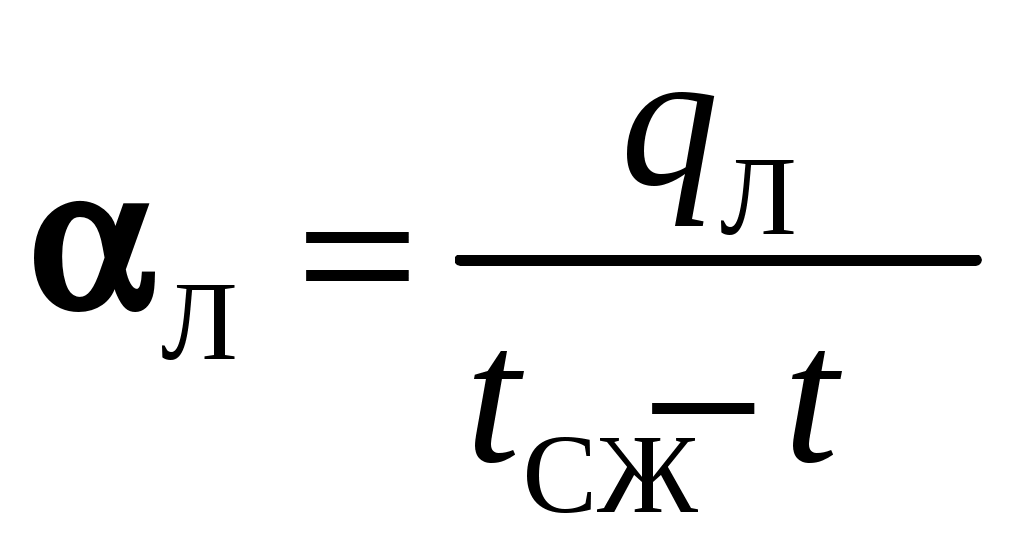 , т.е. используется закон Ньютона-Рихмана, причем
, т.е. используется закон Ньютона-Рихмана, причем 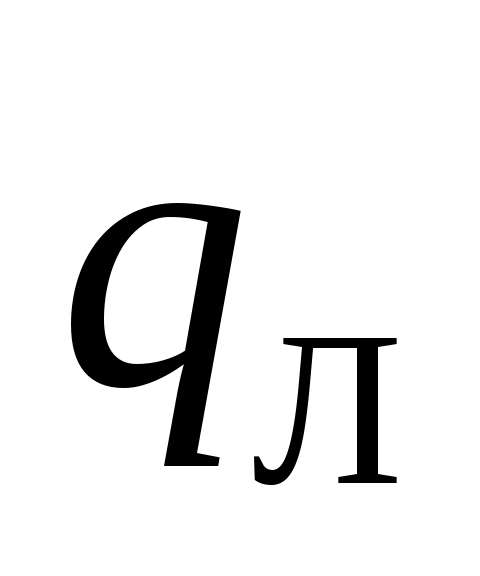 определяется по формулам теплообмена излучением, например, по (10.3). Этот метод широко распространен при расчетах теплообмена конвективных поверхностей нагрева в паровом котле, размещенных в зоне высоких температур дымовых газов. Если поверхность омывается капельной жидкостью, то
определяется по формулам теплообмена излучением, например, по (10.3). Этот метод широко распространен при расчетах теплообмена конвективных поверхностей нагрева в паровом котле, размещенных в зоне высоких температур дымовых газов. Если поверхность омывается капельной жидкостью, то 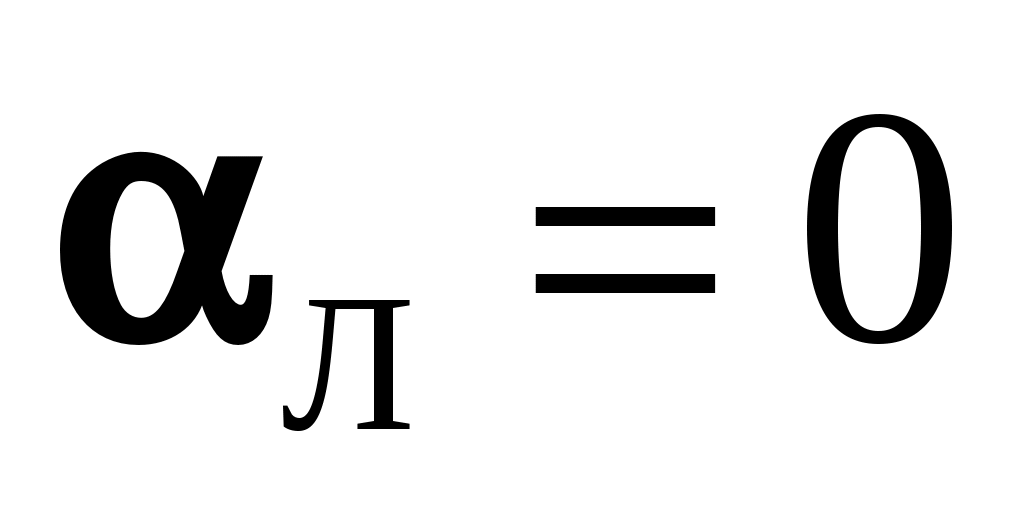 .
.

Рис. 10.1 Рис. 10.2
Ввиду того, что оба газа присутствуют в объеме одновременно, степень черноты смеси должна складываться из степеней черноты отдельных компонентов. Однако частично полосы излучения этих газов совпадают, в связи с чем итоговая степень черноты газового объема будет несколько меньше их суммы на величину
Зная
 .
.Но газовый объем огражден поверхностью, которая имеет свою температуру
, поэтому
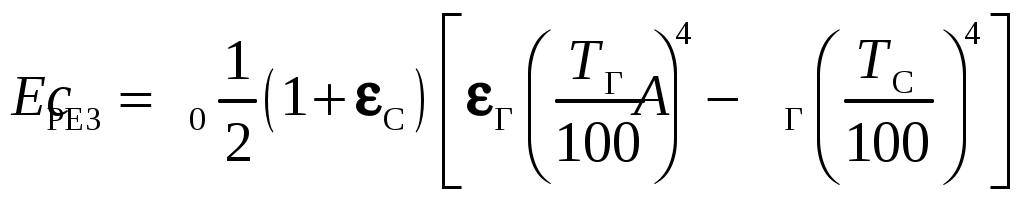 , (10.3)
, (10.3)где
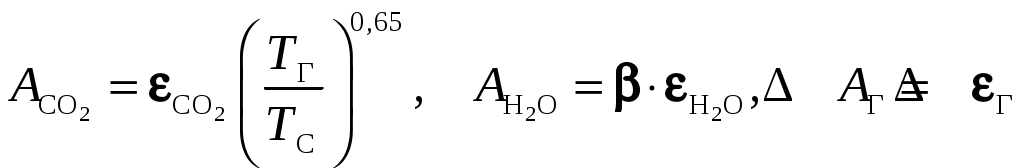 , причем
, причем В более сложных случаях, например, при теплообмене излучением между газом и размещенным в нем пучком труб, расчет
где d – внешний диаметр труб пучка;
Приведенным методом расчета пользуются при сжигании природного или искусственного газов. При камерном сжигании твердого (в виде пыли) и жидкого топлив расчет ведется по методике, основанной на применении закона Бугера, записанного в форме
– оптическая толщина среды.
10.2. Расчет радиационно-конвективного теплообмена.
При размещении поверхности теплообмена в высокотемпературном потоке газа необходимо кроме конвекции учитывать и излучение. В этом случае применяется метод эквивалентного или эффективного коэффициента теплоотдачи, в котором в качестве основного принимают процесс конвективного теплообмена (теплоотдачи), характеризуемого коэффициентом

