. Составим отношение , его обозначают и называют степенью черноты серого тела, т.е. .

Тогда можно получить: 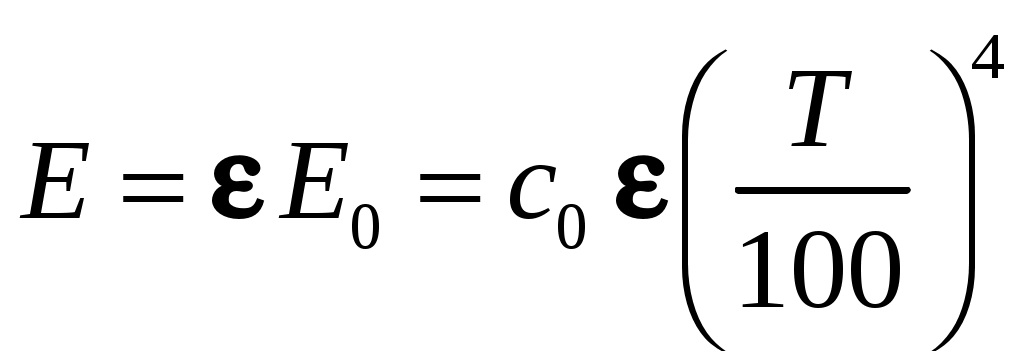. (9.11)

3. Закон Кирхгофа. Он устанавливает соотношение между излучательной и поглощательной способностями серых и абсолютно черного тел. Рассмотрим систему из серого и абсолютно черного тел (рис. 9.3,б). Считаем, что все лучи с одного тела падают на другое. Согласно определению для серого тела результирующий поток запишется: . Но в данном случае , поэтому . При равновесном излучении и или , отсюда . (9.12)

Формулировка закона: отношение плотности потока излучения серого тела при некоторой температуре к его коэффициенту поглощения не зависит от природы тела и равно плотности потока излучения абсолютно черного тела при той же температуре.

Сравнивая соотношение (9.12) с выражением для степени черноты, можно видеть, что , (9.13)

т.е. степень черноты серого тела численно равна его коэффициенту поглощения. Этот вывод часто называют следствием из закона Кирхгофа. Он показывает, что чем больше тело поглощает, тем больше оно и излучает. Потому, если белое тело ничего не поглощает, то ничего и не излучает.

4. Закон косинусов Ламберта

Рассмотрим единичную площадку (рис. 9.3,в). Проведем нормаль к этой площадке. В направлении нормали выделим элементарный телесный угол

---

. Обозначим поток излучения в пределах этого телесного угла . Выберем произвольное направление под углом к нормали и в этом направлении также выделим элементарный телесный угол . Обозначим поток излучения в пределах этого угла через . Экспериментально установлено, что . (9.14)

Это и есть аналитическое выражение закона косинусов Ламберта, записанного в дифференциальной форме. Он гласит: плотность потока излучения в пределах элементарного телесного угла в направлении к нормали равен плотности потока излучения в пределах угла в направлении нормали, умноженной на косинус этого угла .

Воспользуемся соотношением (9.1) и выразим из него яркость излучения: 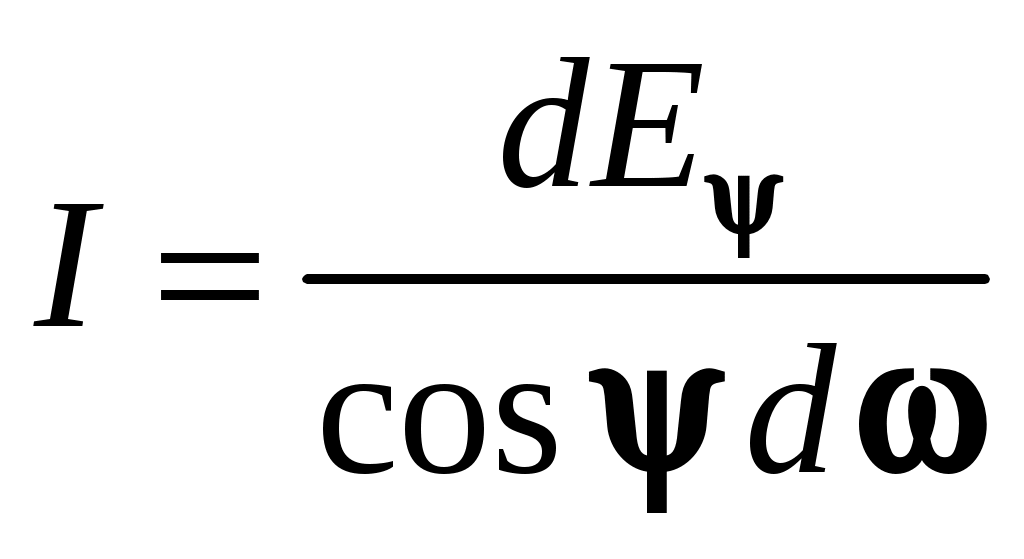и подставим в него (9.14), получим: , т.е. яркость излучения не зависит от направления. Такое излучение называется диффузным. Следовательно, если излучение подчиняется закону косинусов Ламберта, то оно является диффузным, и наоборот, если излучение диффузное, то оно подчиняется закону косинусов Ламберта.

Получим интегральную форму закона Ламберта. Согласно уравнению (9.2) 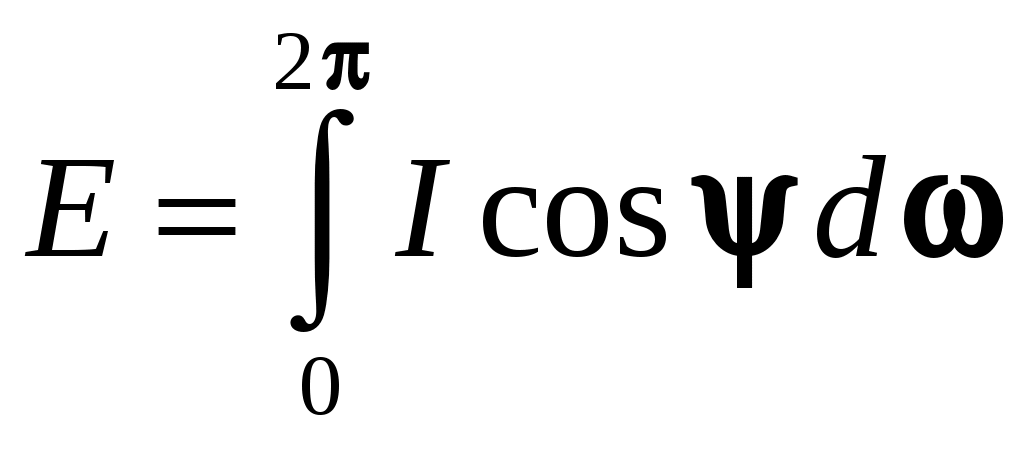. Но для диффузного излучения 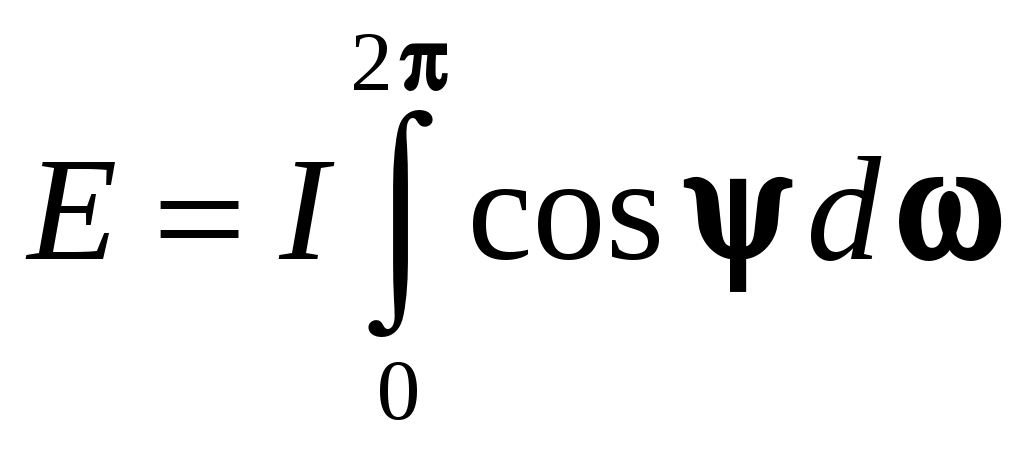, поэтому , а после интегрирования или

---

. (9.15)

Следовательно, для диффузионного излучения яркость излучения меньше плотности потока излучения в раз. С учетом (9.15) можно получить еще одну форму закона косинусов Ламберта:

или . (9.16)

Обычно в таком виде и используется закон косинусов Ламберта.
9.3. Отдельные задачи теплообмена излучением между двумя телами, разделенными прозрачной средой

При рассмотрении отдельных задач теплообмена излучением будем считать:

1. 
   Режим стационарный, тела разделены прозрачной средой.
   
2. 
   Тепло передается только излучением; теплопроводность и конвекция отсутствуют.
   
3. 
   Поверхности тел – изотермические, а сами тела – серые.
   
4. 
   Излучение тел диффузное, т. е. подчиняется закону косинусов Ламберта.
   
5. 
   и 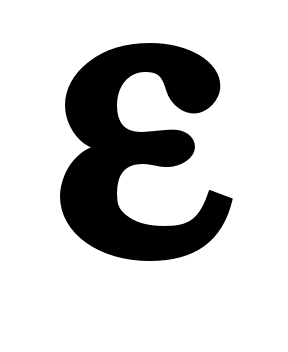не зависят от температуры.
   

9.3.1. Теплообмен излучением между двумя телами

с плоскопараллельными поверхностями

Рассмотрим два тела с плоскопараллельными поверхностями (рис. 9.4,а). Пусть для первого тела известны: собственное излучение , коэффициент поглощения , температура . Аналогично для второго тела заданы . Считаем, что .

Применяя метод сальдо с учетом законов Стéфана-Больцмана и Кирхгофа можно получить следующее выражение для результирующего потока излучением с первого тела на второе:

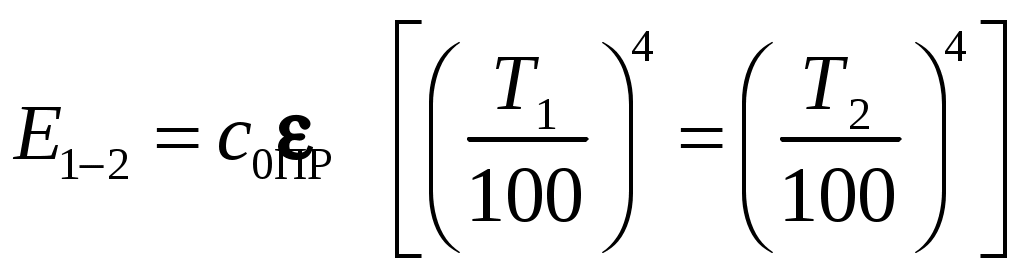, (9.17)

где 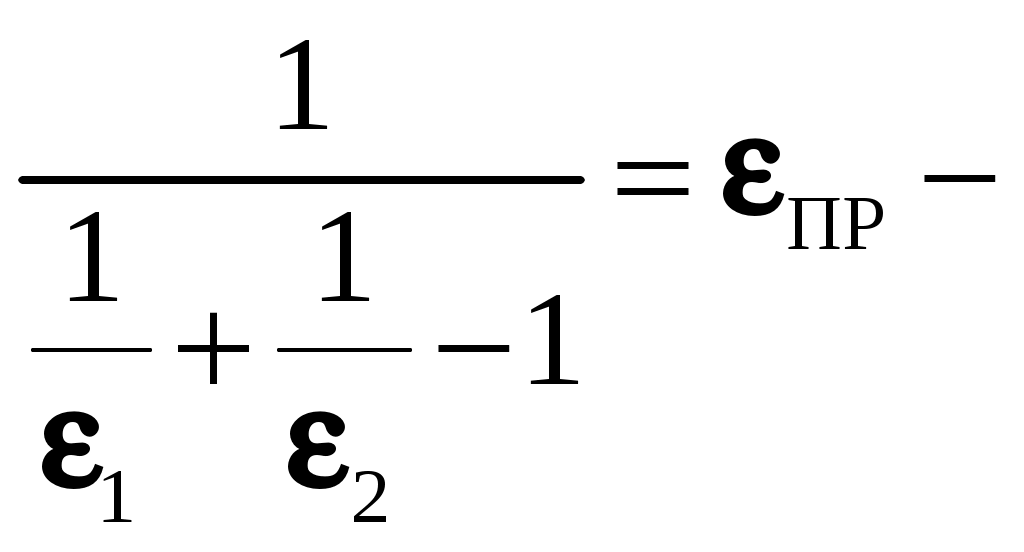приведенная степень черноты.

Влияние экранов

Вновь рассмотрим два тела с плоскопараллельными поверхностями. Между ними размещено тонкое непрозрачное плоское тело, параллельно телам 1 и 2, которое и называется экраном (рис. 9.4,

---

б).

Пусть известны: для первого тела ;

для второго тела ;

для экрана .

В этом случае результирующий поток будет равен:

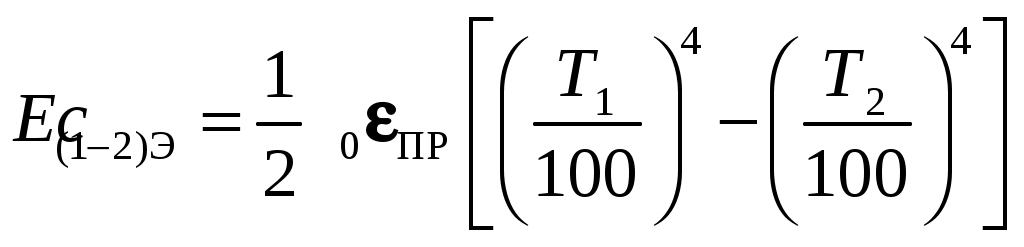. (9.18)

Уравнение получено в предположении, что 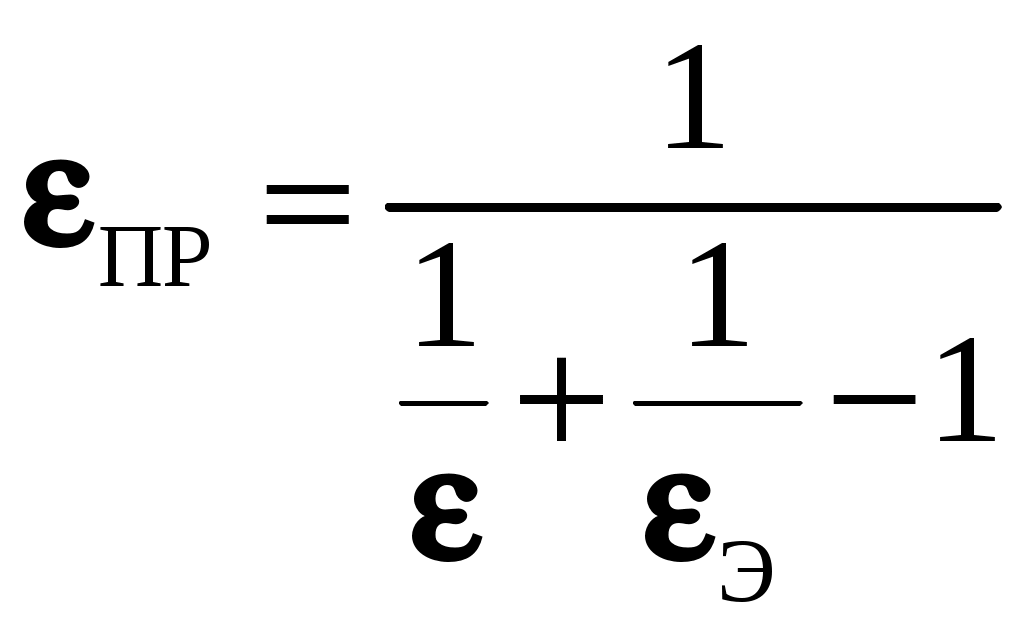. Тогда , а температура экрана равна: .

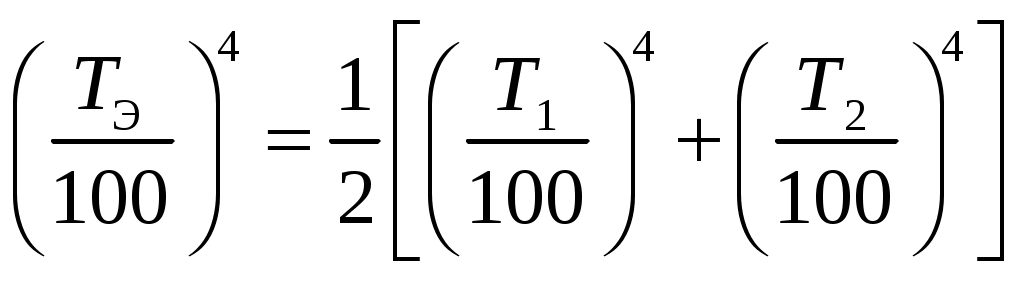Если принять, что , то , т.е. установка такого экрана уменьшит тепловой поток излучением в 2 раза. Можно показать, что установка двух таких экранов уменьшит тепловой поток излучением в 3 раза и т.д.

9.3.2. Теплообмен излучением между телом и его оболочкой

Пусть тело 1 целиком расположено в полости другого тела 2, которое и называется оболочкой (рис. 9.4, в).


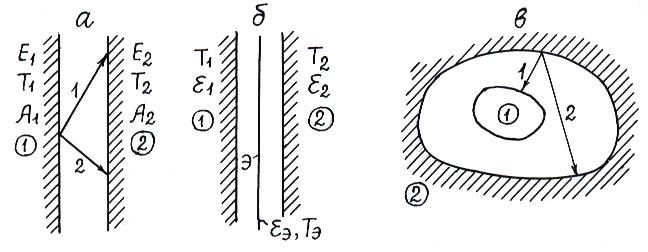
Рис. 9.4
Для первого тела известны: , а для второго тела соответственно . Для определенности считаем, что . Необходимо найти результирующий тепловой поток с первого тела на второе . Согласно определению . Этот случай отличается от предыдущего тем, что не все лучи со второго тела упадут на первое. Действительно (рис. 9.8), луч а падает на первое тело, а луч б проходит мимо. Поэтому . Введем некоторый коэффициент

---

так, чтобы . В этом случае коэффициент характеризует часть лучистой энергии, которая падает со второго тела на первое; его называют угловым коэффициентом излучения. С учетом этого соотношения

. (9.19)

Применяя метод сальдо с учетом законов Стéфана-Больцмана и Кирхгофа можно получить следующее выражение для результирующего потока излучением с первого тела на второе:

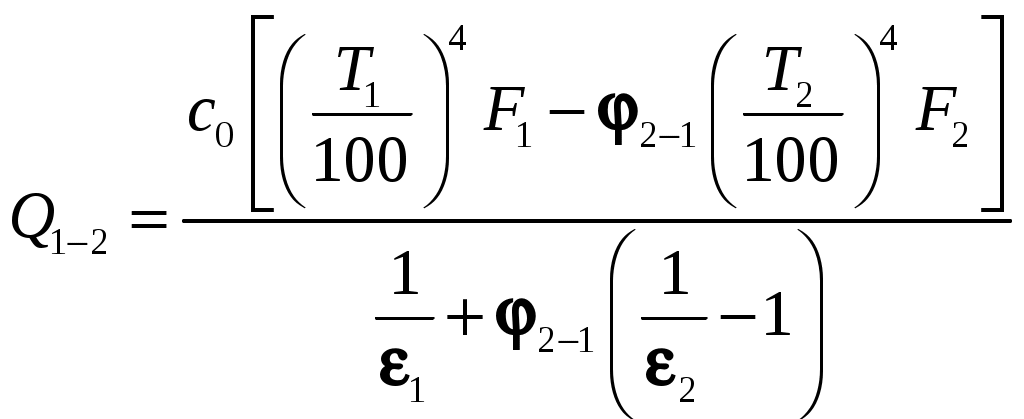. (9.20)

Если , то результирующий тепловой поток излучением , а это значит, что числитель предыдущего соотношения равен нулю, т.е.

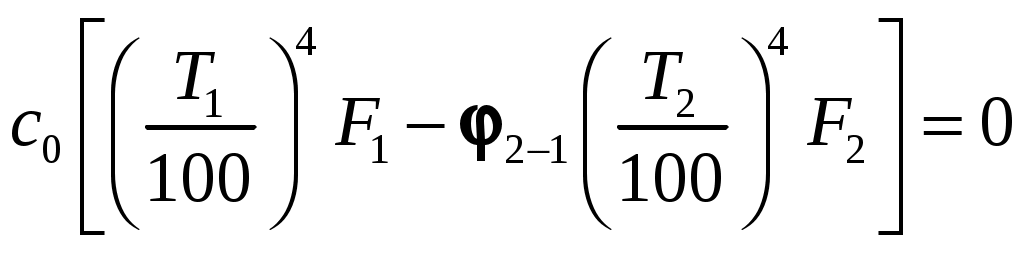, откуда . Определив , из уравнения (9.25) можно найти:
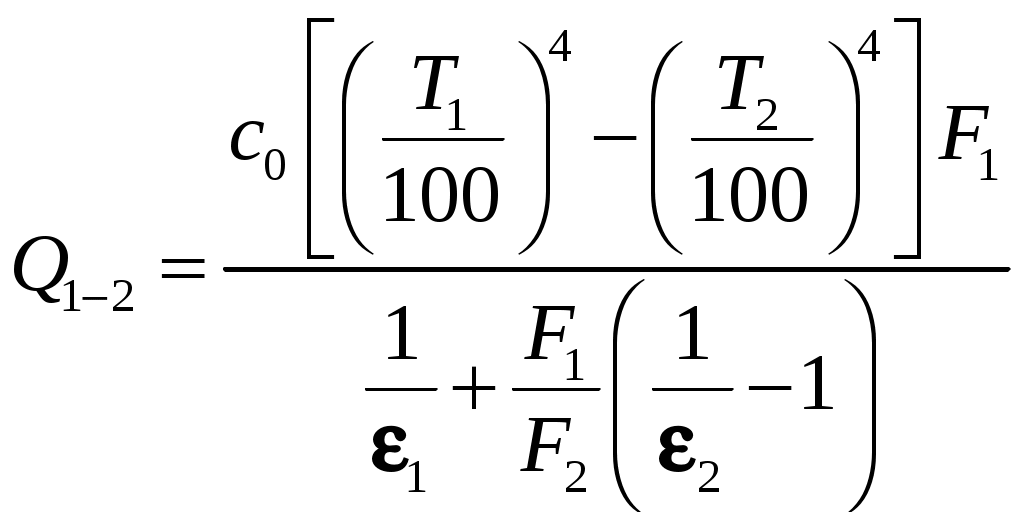, или после введения приведенной степени черноты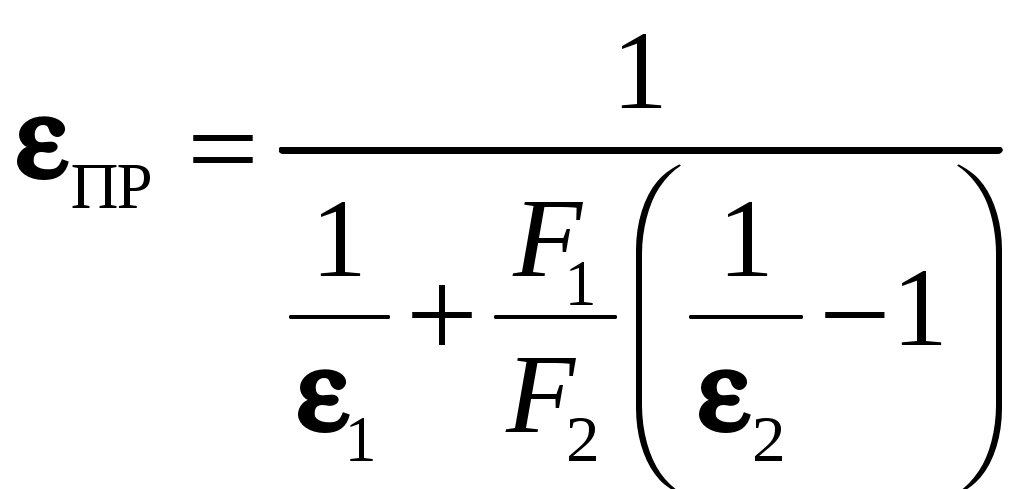

можно записать окончательное решение в следующей стандартной форме:
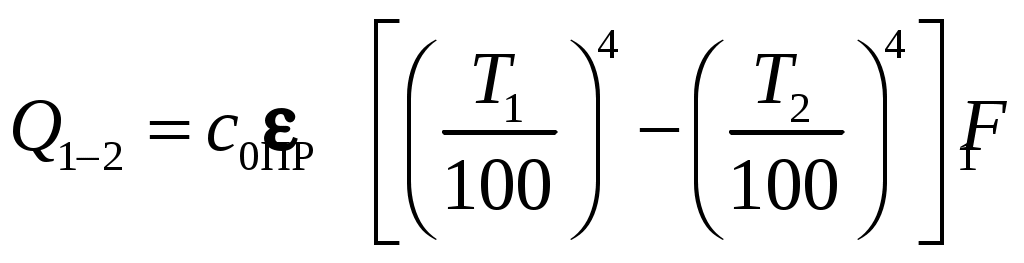. (9.21)
Частные случаи.

1. Пусть 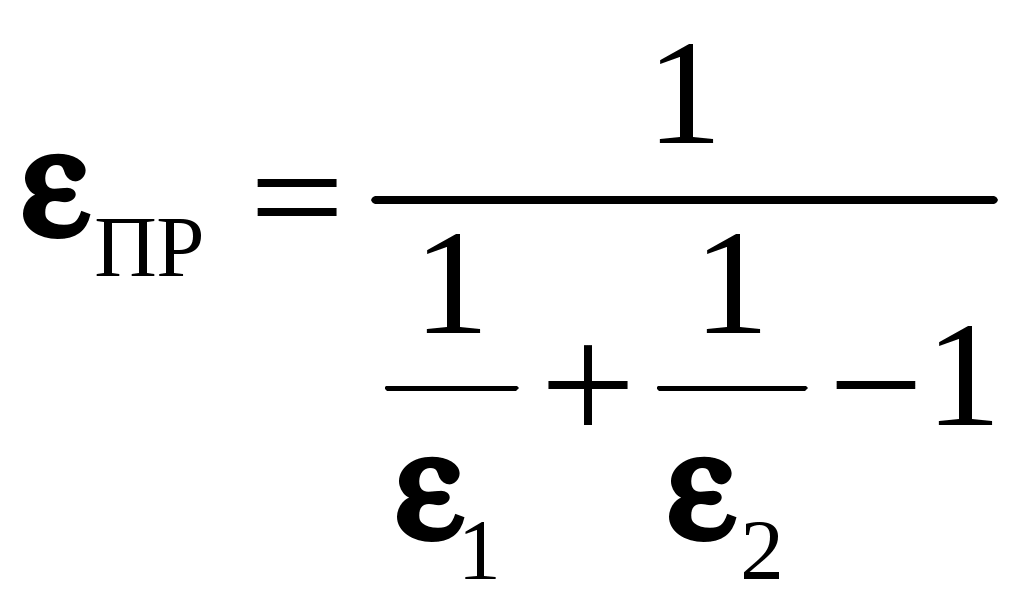(см. рис. 9.5). Тогда и , т.е. ничем не отличается от такового для двух параллельных тел.
2. Пусть теперь , в этом случае и .

---

Смотрите также файлы

• Технического состояния.docx

• Галинная Е. В.docx

• Приговор как акт правосудия по уголовным делам.docx

• Литературные сказки.docx

• Курсовая работа по специальности 38. 02. 04 Коммерция (в торговле).docx