ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 31
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 9.5
9.3.3 Теплообмен излучением между двумя телами, произвольно
расположенными в пространстве
Р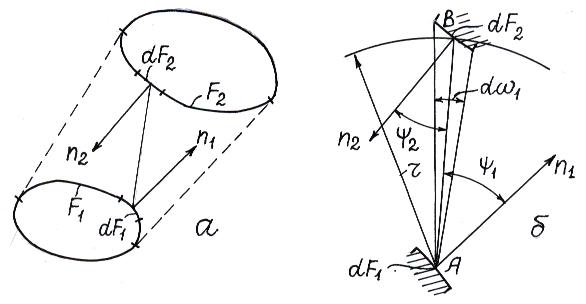 ассмотрим тело 1 и тело 2, произвольно расположенные в пространстве. Очевидно, что в теплообмене будут участвовать лишь поверхности
ассмотрим тело 1 и тело 2, произвольно расположенные в пространстве. Очевидно, что в теплообмене будут участвовать лишь поверхности 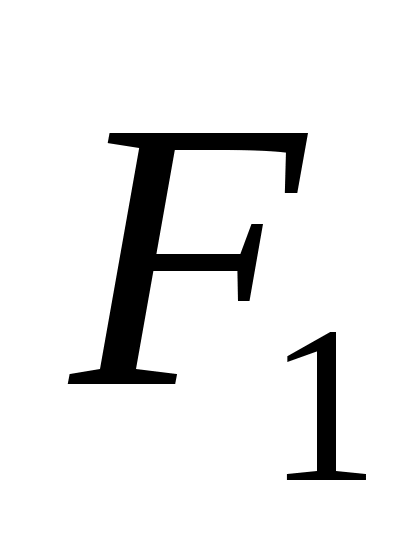 и
и 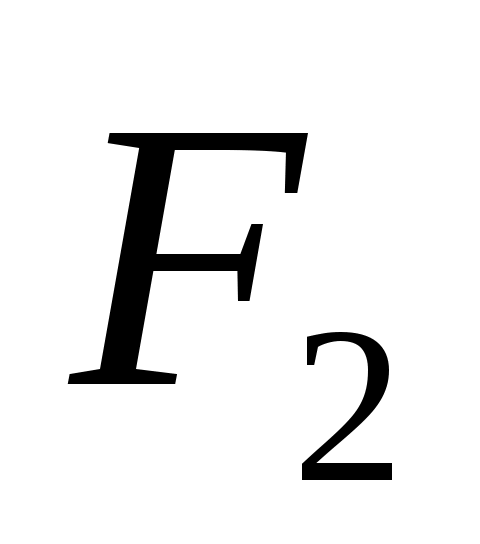 , обращенные друг к другу (рис. 9.6), причем не все лучи с каждого тела достигнут другого. Поэтому введем угловые коэффициенты, характеризующие долю полного излучения, которая падает с одного тела на другое:
, обращенные друг к другу (рис. 9.6), причем не все лучи с каждого тела достигнут другого. Поэтому введем угловые коэффициенты, характеризующие долю полного излучения, которая падает с одного тела на другое: 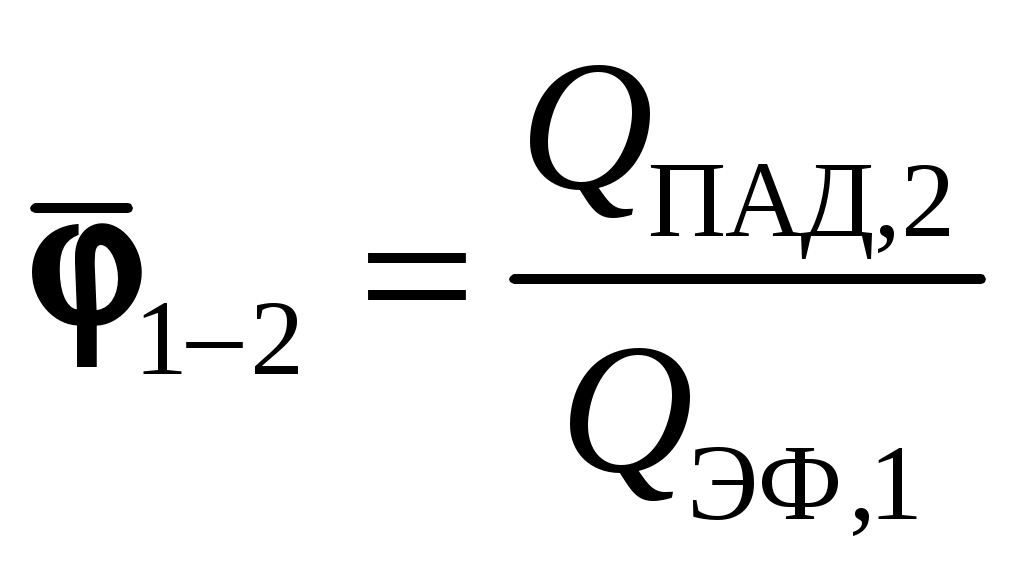 – средний угловой коэффициент излучения с первого тела на второе,
– средний угловой коэффициент излучения с первого тела на второе,  – поток излучением с поверхности
– поток излучением с поверхности 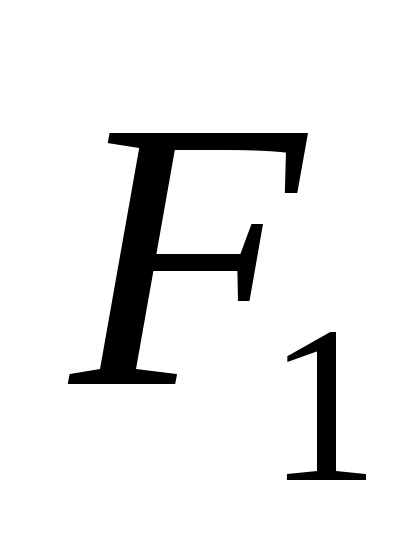 в направлении
в направлении 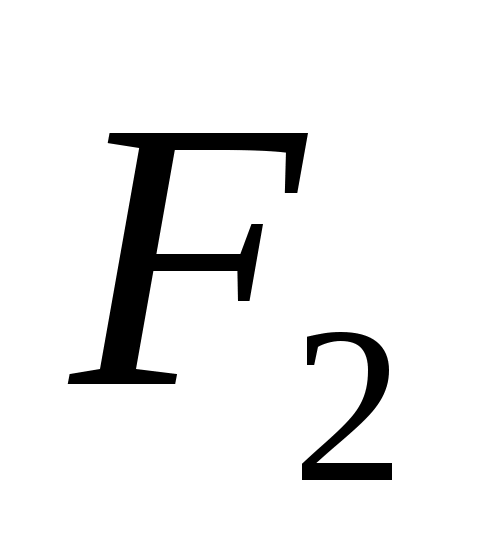 ,
, 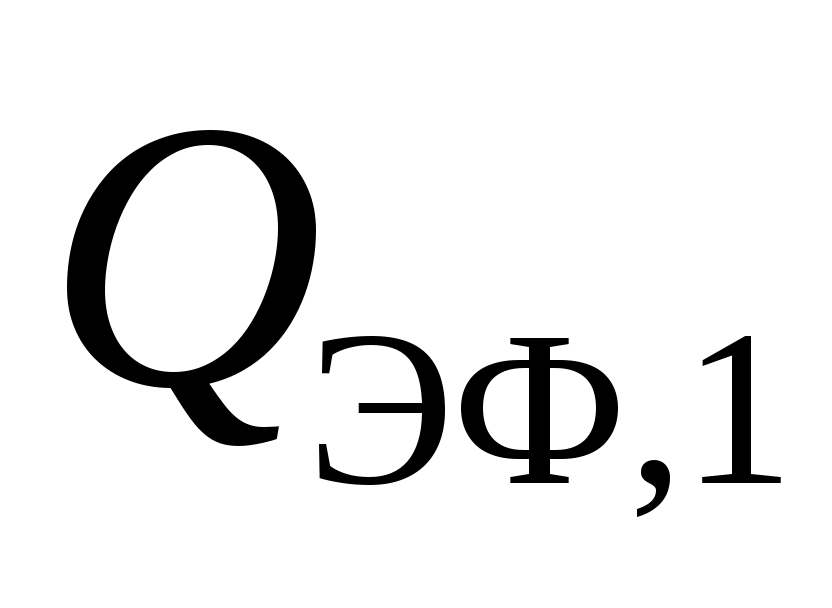 – эффективный поток излучением с поверхности
– эффективный поток излучением с поверхности 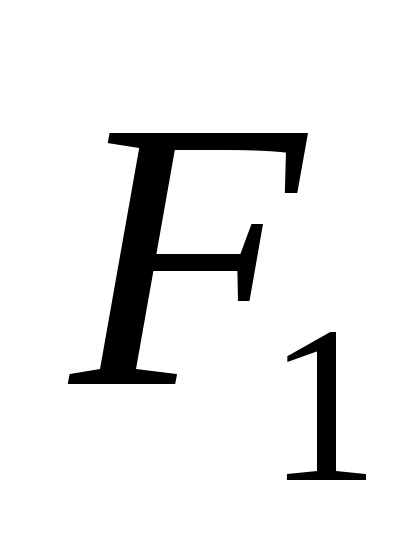 ;
;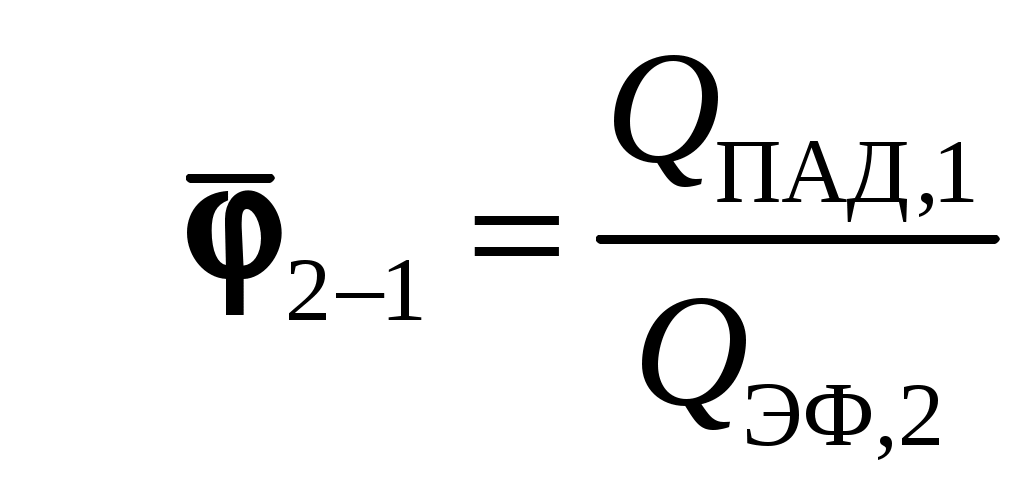 – средний угловой коэффициент излучения со второго тела на первое,
– средний угловой коэффициент излучения со второго тела на первое,  – поток излучением с поверхности
– поток излучением с поверхности 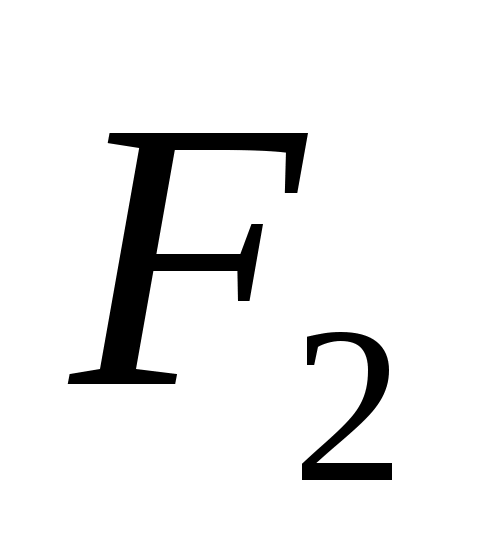 в направлении
в направлении 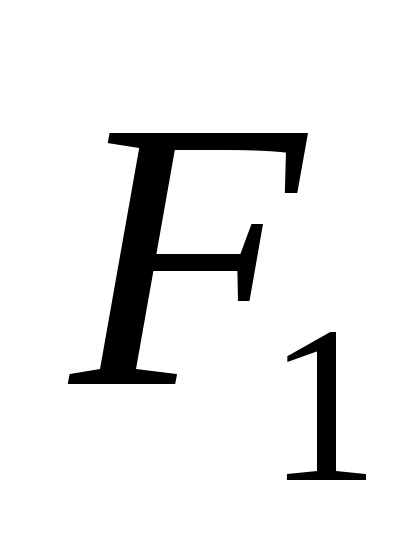 ,
, 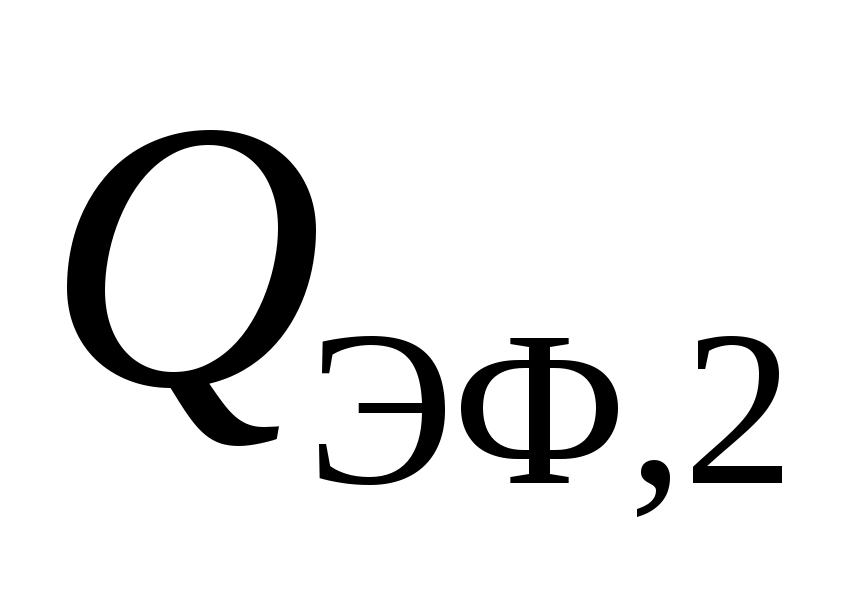 – эффективный поток излучением с поверхности
– эффективный поток излучением с поверхности 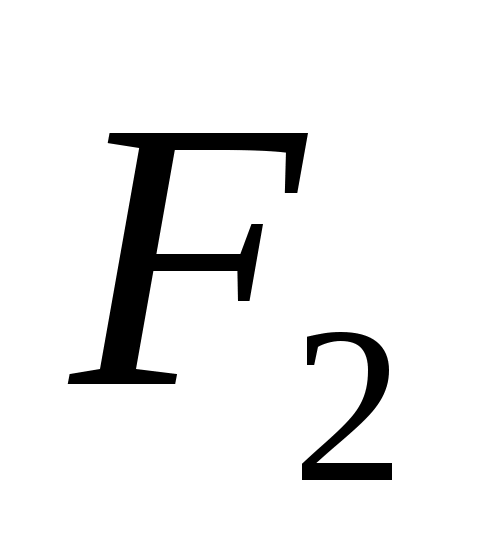 .
.
Отсюда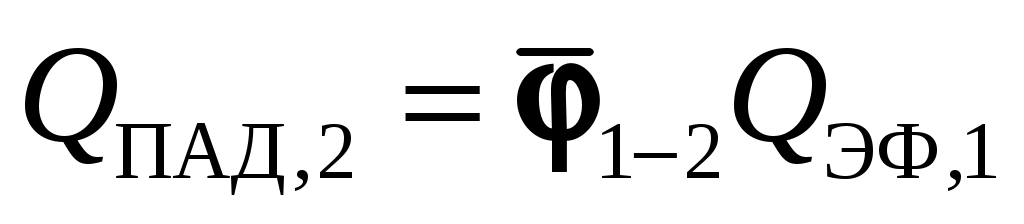 , а
, а 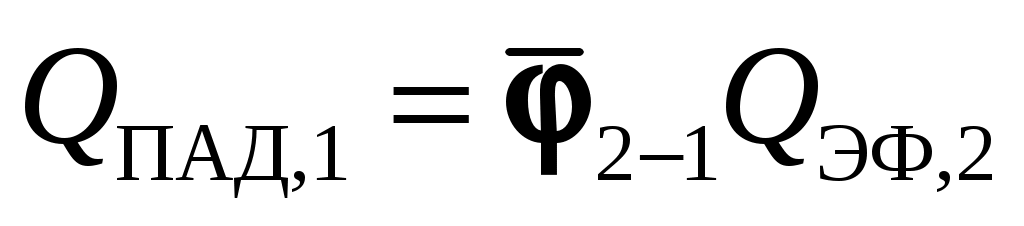 , тогда разность между ними и будет искомым тепловым потоком между телами 1 и 2:
, тогда разность между ними и будет искомым тепловым потоком между телами 1 и 2: 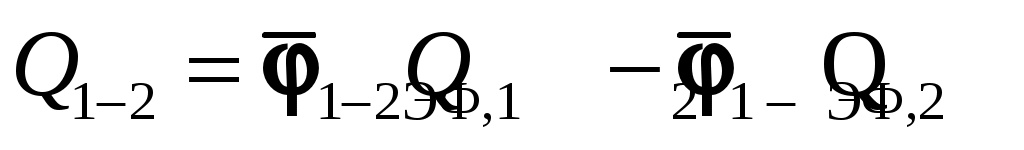
. Применяя метод сальдо Рис. 9.6
и законы Стефана-Больцмана и Кирхгофа, можно получить следующее выражение для результирующего потока излучением, записанное в стандартной форме:
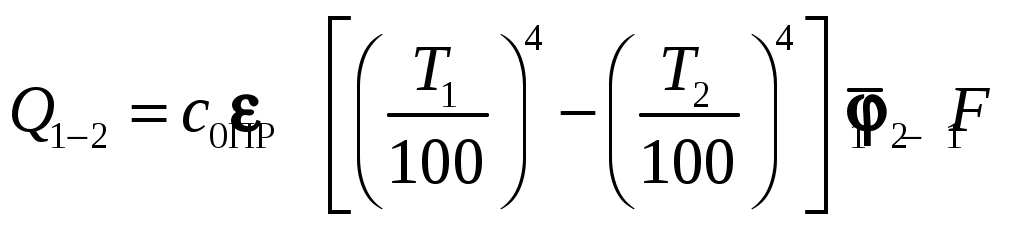 (9.22)
(9.22)
или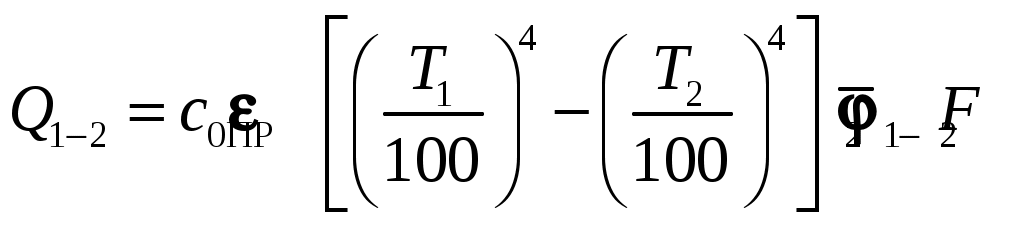 , (9.23)
, (9.23)
где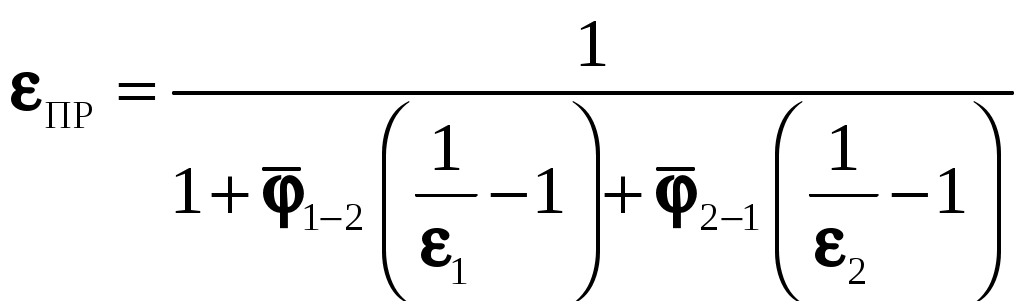 (9.24)
(9.24)
Из полученных формул следует, что для расчета теплообмена излучением в общем случае необходимо знать угловые коэффициенты излучения. Рассмотрим их более подробно.
9.3.4. Геометрические свойства угловых коэффициентов излучения
Угловые коэффициенты излучения, если среда прозрачная, зависят только от геометрических свойств системы, а именно размеров тел, расстояния между ними и ориентации их в пространстве. Они обладают следующими свойствами.
1. Свойство взаимности
Из уравнений (9.22) и (9.23) можно видеть, что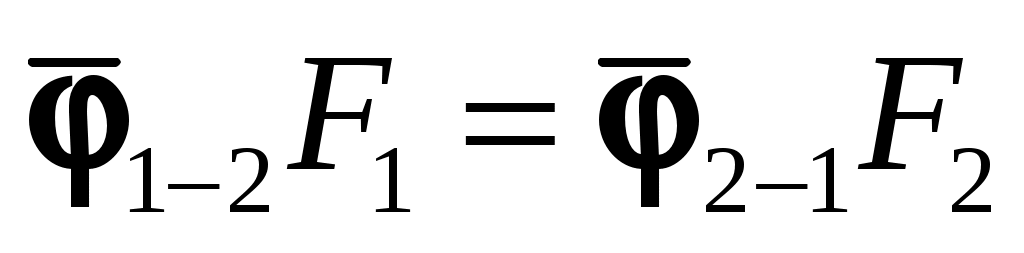 .
.
Здесь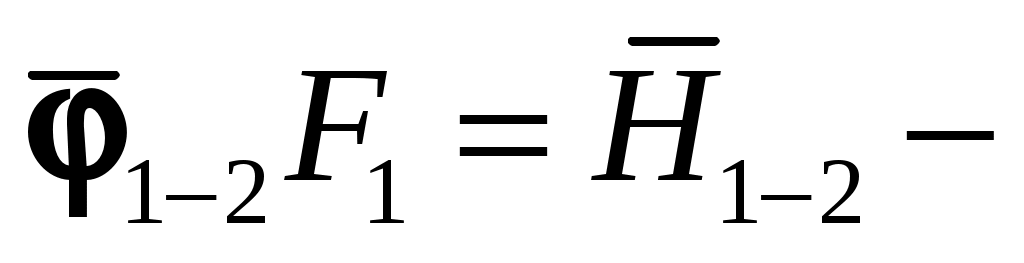 взаимная поверхность излучения с первого тела на второе,
взаимная поверхность излучения с первого тела на второе, 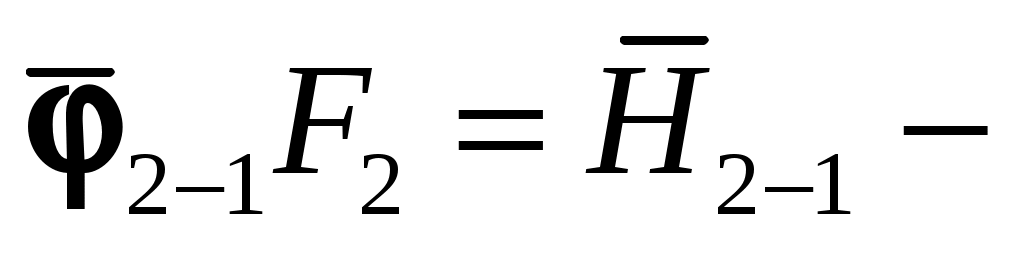 взаимная поверхность излучения со второго тела на первое. Отсюда
взаимная поверхность излучения со второго тела на первое. Отсюда 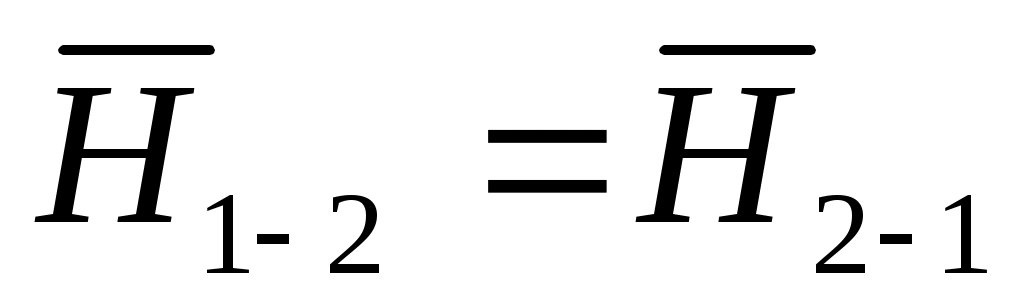 , т.е. взаимные поверхности излучения тел равны между собой. В этом и состоит свойство взаимности угловых коэффициентов излучения.
, т.е. взаимные поверхности излучения тел равны между собой. В этом и состоит свойство взаимности угловых коэффициентов излучения.
2. Свойство замыкаемости (замкнутости) тел
Рассмотрим замкнутую систему, состоящую из n тел. Пусть для первого тела эффективное излучение равно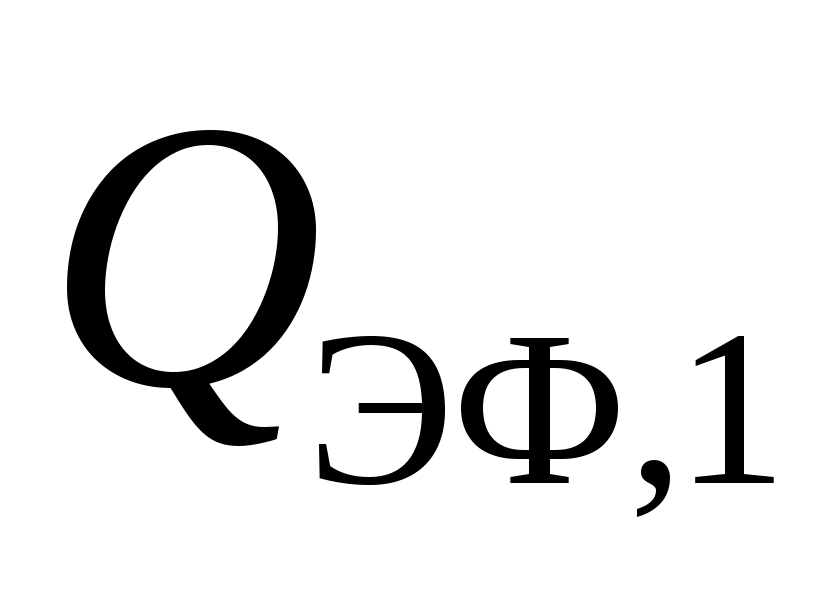 , а падающее излучение с него на каждое из остальных, включая и само тело (в случае самооблучения),
, а падающее излучение с него на каждое из остальных, включая и само тело (в случае самооблучения), 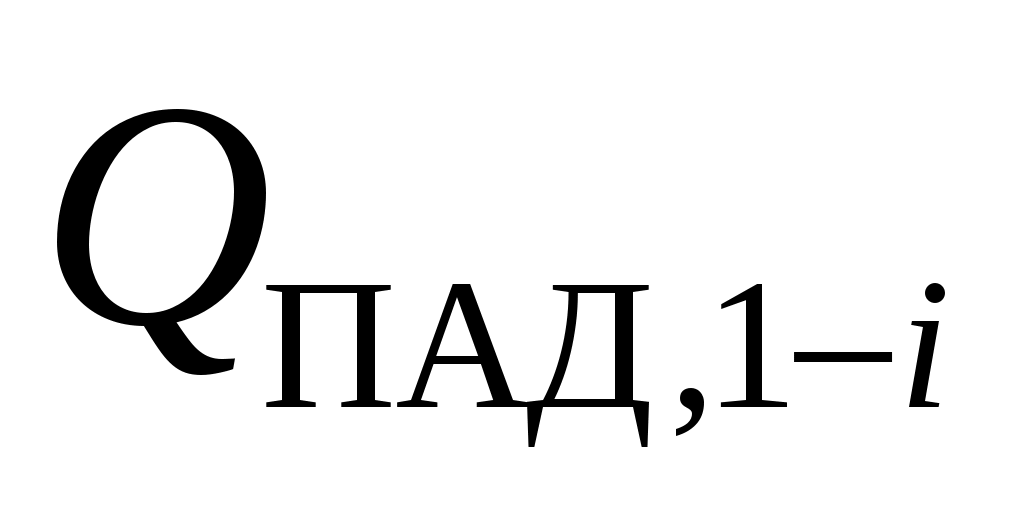 , где
, где 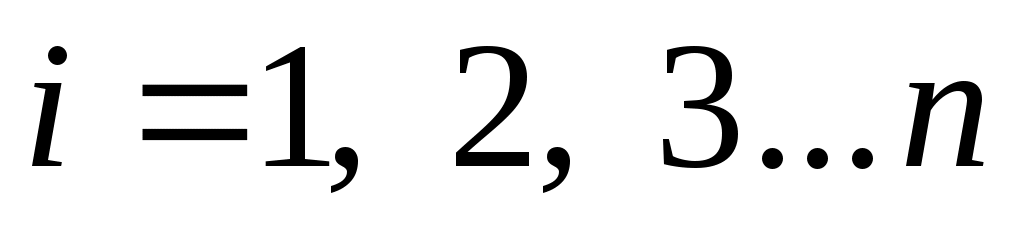 . Так как система замкнутая, то на основании закона сохранения энергии
. Так как система замкнутая, то на основании закона сохранения энергии 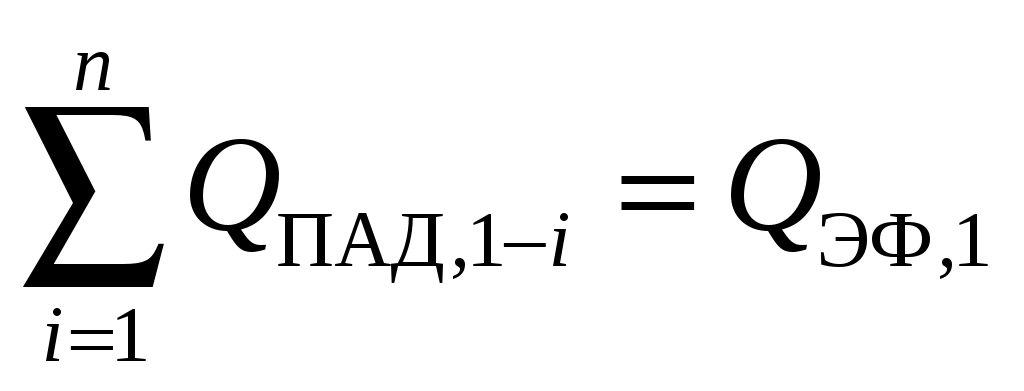 , но согласно определению
, но согласно определению 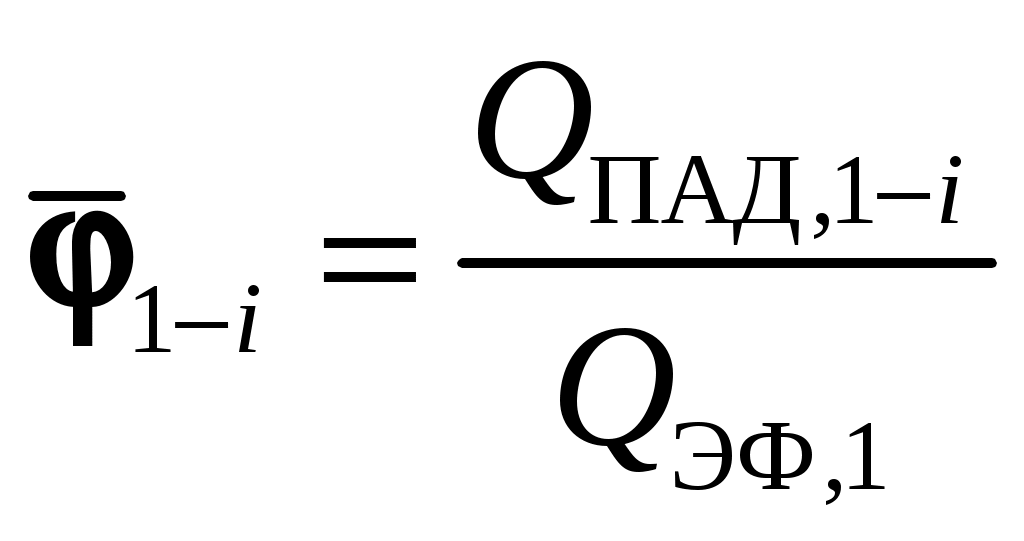 или
или 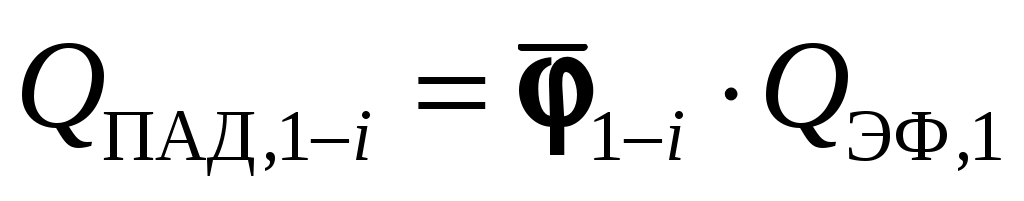
, тогда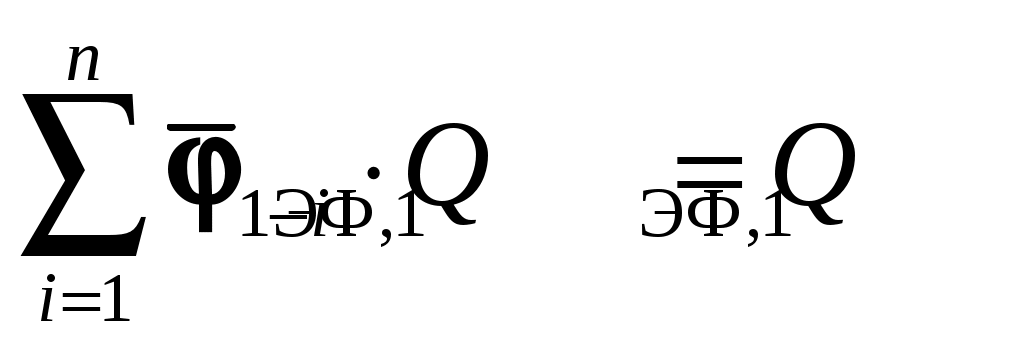 , а после сокращения на
, а после сокращения на 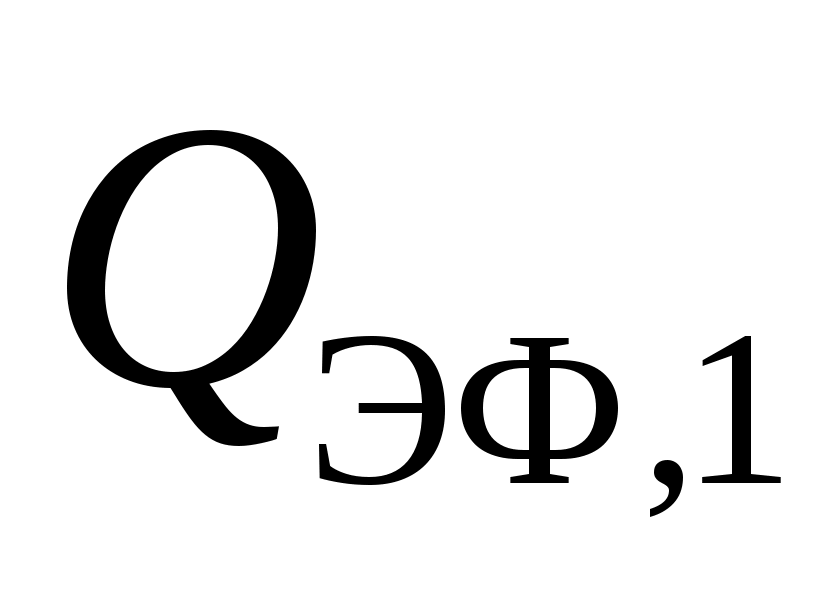 получаем:
получаем: 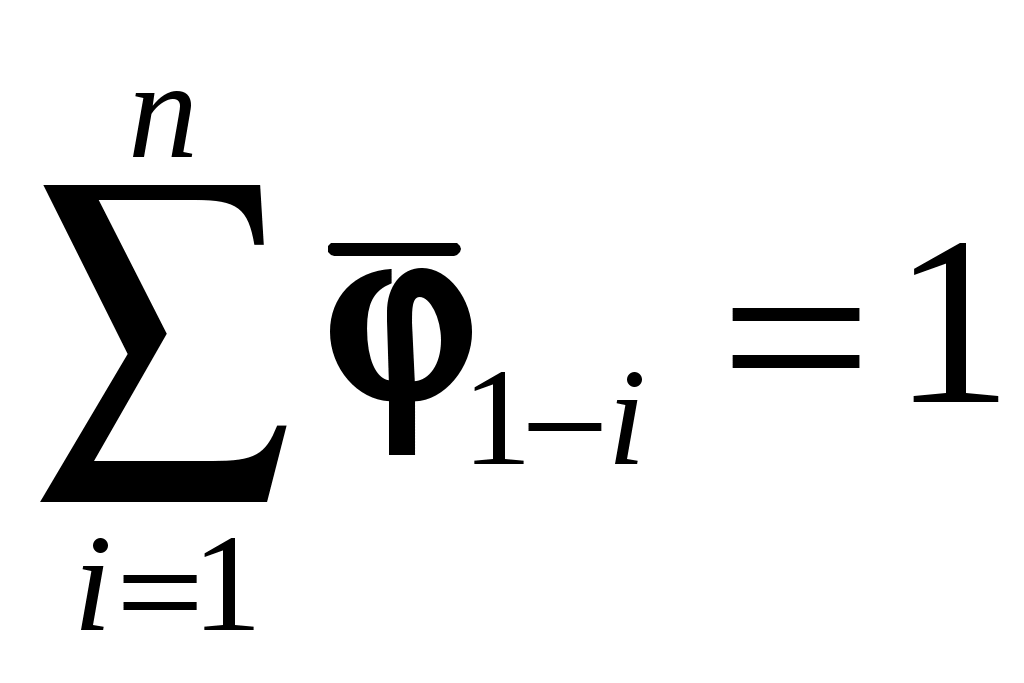 , т.е. для замкнутой системы сумма угловых коэффициентов излучения с какого-либо тела на все остальные, включая и само тело, равна единице. В этом и состоит свойство замыкаемости угловых коэффициентов излучения.
, т.е. для замкнутой системы сумма угловых коэффициентов излучения с какого-либо тела на все остальные, включая и само тело, равна единице. В этом и состоит свойство замыкаемости угловых коэффициентов излучения.
3. Свойство затеняемости
Рассмотрим два тела (рис. 9.7), между которыми размещено третье непрозрачное тело такое, что перегораживает все лучи с первого тела на второе и обратно. Тогда получаем: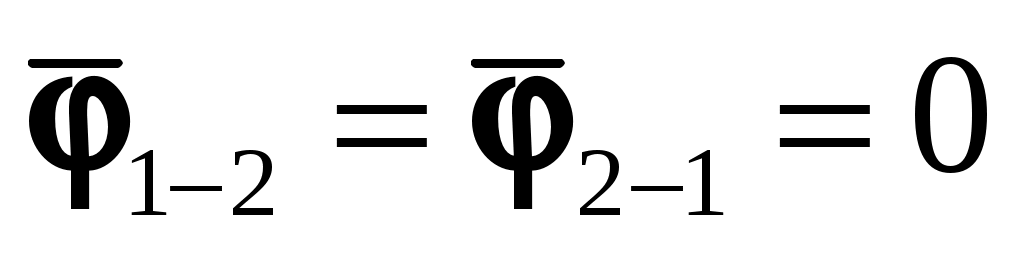 и
и 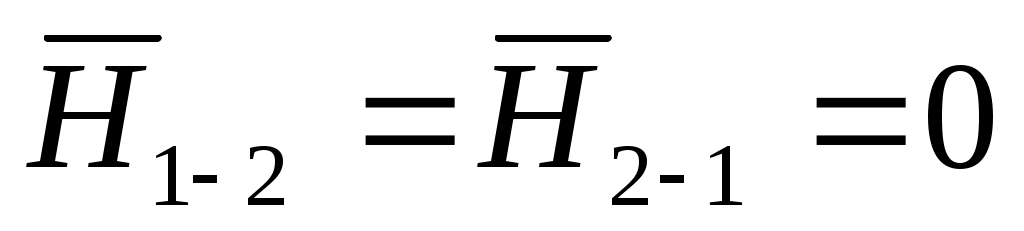 . В этом и состоит свойство затеняемости. Особенно величественно оно проявляется во время полного солнечного затмения.
. В этом и состоит свойство затеняемости. Особенно величественно оно проявляется во время полного солнечного затмения.
Рис. 9.7
9.3.5. Методы определения угловых коэффициентов излучения
Существуют различные методы определения угловых коэффициентов излучения, среди которых сравнительно простым и достаточно эффективным является метод поточной алгебры.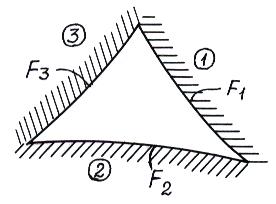 В этом случае рассматривают замкнутую систему, состоящую из трех невогнутых тел: 1, 2 и 3 (рис. 9.8). Для них известны поверхности
В этом случае рассматривают замкнутую систему, состоящую из трех невогнутых тел: 1, 2 и 3 (рис. 9.8). Для них известны поверхности 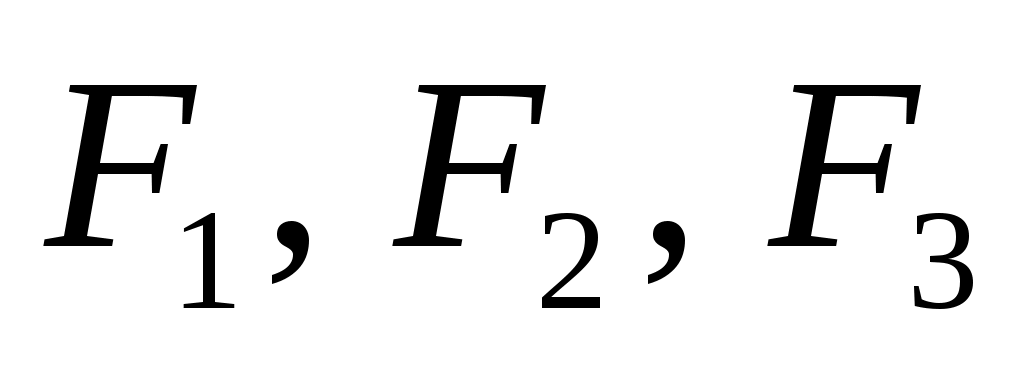 . Считая, что размеры тел в направ-
. Считая, что размеры тел в направ-
Рис. 9.8 лении оси z велики по сравнению с их поперечными размерами, что позволяет пренебречь излучением с торцов, и используя свойства замыкаемости и взаимности, можно получить
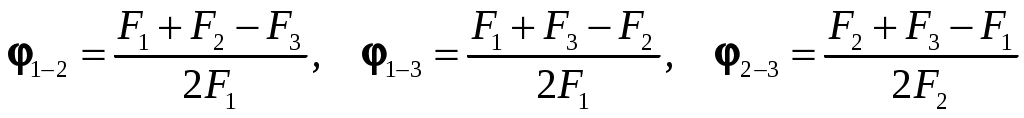 и т.д.
и т.д.
10. ОБЪЕМНОЕ ИЗЛУЧЕНИЕ
Газы и пары обладают низкими коэффициентами поглощения, поэтому в излучении и поглощении участвуют все частицы (молекулы, атомы) газового объема. Такое излучение и называется объемным. Кроме того, для них характерно выборочное или селективное излучение и поглощение.
10.1. Особенности излучения газов и паров
В инженерной практике с излучением газов и паров встречаются в металлургических печах и топках паровых котлов, в которых теплота выделяется при сжигании органических топлив: твердых (при камерном сжигании угля), жидких (например, мазута) и газообразных (природного или искусственного газов). Во всех случаях при полном сжигании образуется углекислый газ (СО2), а при неполном – угарный газ (СО). Для сжигания топлива используется кислород воздуха, который подводится всегда с некоторым избытком. Поэтому в топке содержится О2 и, естественно, азот N2. В атмосферном воздухе всегда есть влага, поэтому в топочной смеси присутствует водяной пар (Н2О). Кроме того, влага может поступать в топку вместе с топливом. При сжигании природного газа возможно присутствие СН4. Иногда вместе с топливом попадают оксиды серы, фосфора и др. В общем случае в топочных газах могут находиться и твердые частицы угольной пыли и золы. Здесь рассмотрим излучение газового объема, не содержащего твердых частиц.
Исследования показали, что излучение и поглощение двухатомных газов (О2, N2) невелико, поэтому их излучение не учитывается. Излучение таких газов, как CO, CH4, S2O3 и др., значительно, но концентрация их мала, поэтому оно тоже не принимается во внимание. Таким образом, в инженерной практике учитывается лишь излучение CO2 и H2O.
Оба газа обладают выборочным излучением. Спектры излучения и поглощения их хорошо изучены. При этом различают тонкую и грубую структуру спектра. В расчетной практике учитывается лишь грубая структура, т.е. самые широкие полосы спектра. С увеличением температуры ширина полос излучения и поглощения увеличивается, что приводит к возрастанию излучательной и поглощательной способностей этих газов. Так как ширина полос для паров воды несколько больше, чем для углекислого газа, то и излучение их больше. Кроме того, излучение и поглощение обоих газов зависит от количества частиц в рассматриваемом объеме, которое определяется парциальным давлением каждого газа, и размерами газового объема, характеризуемого средней длиной пути луча .
.
Следовательно, излучение каждого газа зависит от его природы, температуры, парциального давления P и размера .
.
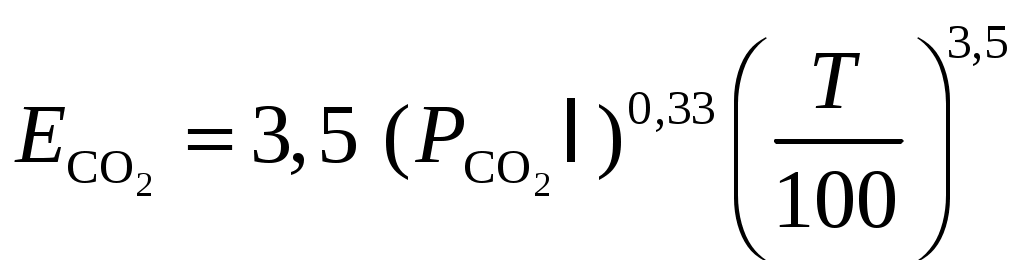 ,
, 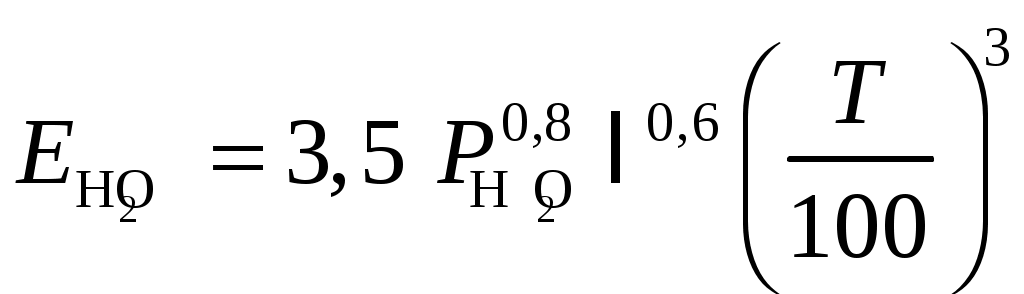 . (10.1)
. (10.1)
Можно видеть, что в обоих случаях излучение газов не подчиняется закону Стéфана-Больцмана. Но обычно газ участвует в теплообмене со стенками топки, экранированной трубами, излучение которых подчиняется закону Стефана-Больцмана. Применение различных законов резко бы усложнило расчеты. Поэтому предполагают, что и излучение газов подчиняется закону четвертой степени, следовательно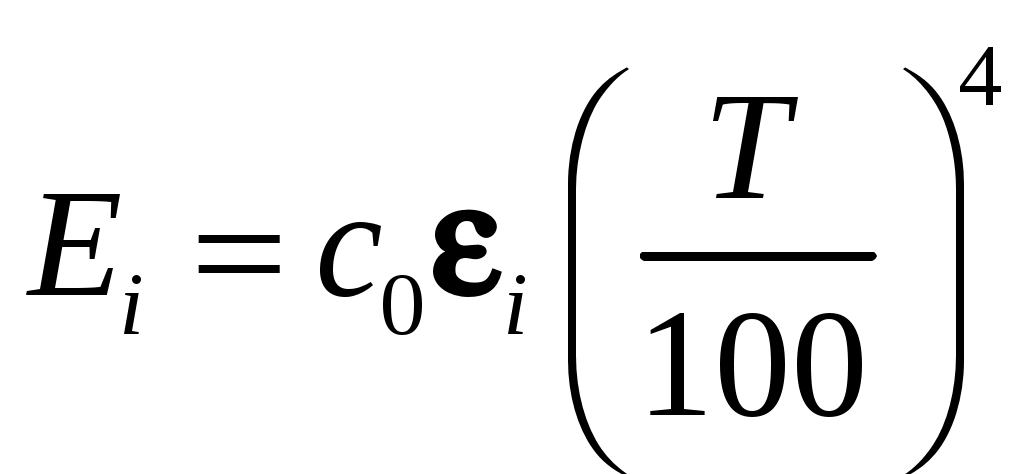 , а все отличие учитывается соответствующим выбором
, а все отличие учитывается соответствующим выбором 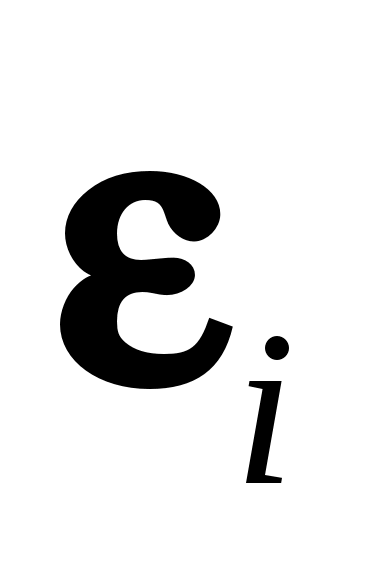 – степени черноты данного газа. Тогда, сравнивая это уравнение с соотношениями (10.1), можно заключить, что
– степени черноты данного газа. Тогда, сравнивая это уравнение с соотношениями (10.1), можно заключить, что 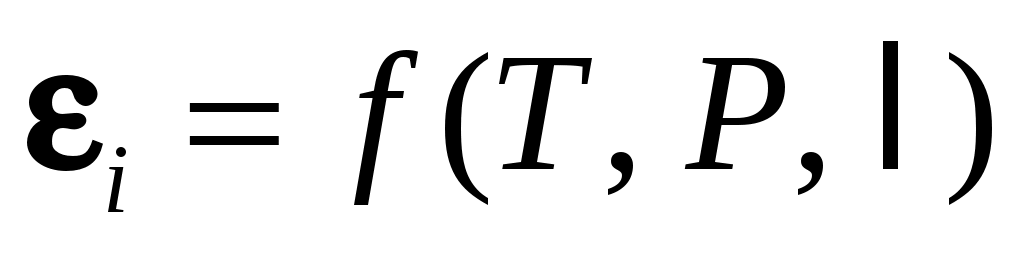 . Для определения
. Для определения 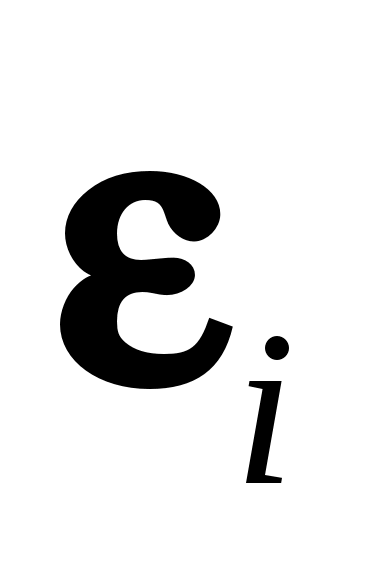 используются номограммы, своя для каждого газа. Но построить такую функцию на плоскости невозможно, поэтому принимают, что
используются номограммы, своя для каждого газа. Но построить такую функцию на плоскости невозможно, поэтому принимают, что 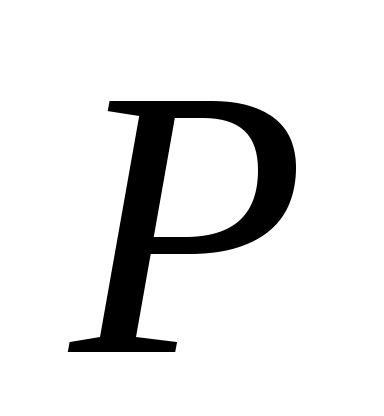 и
и  влияют на
влияют на 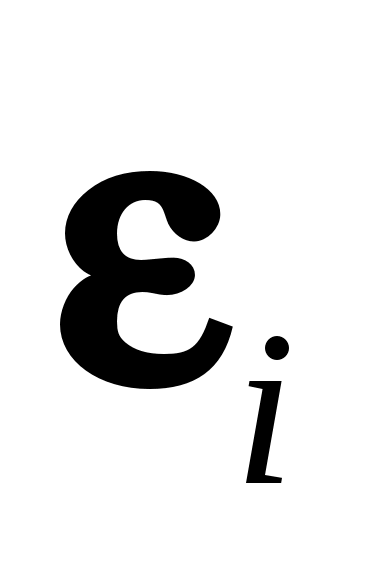 в одной степени, отсюда
в одной степени, отсюда 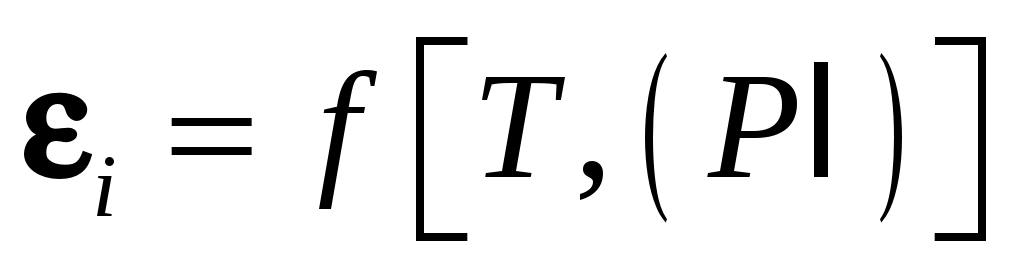 . Такие зависимости и построены в виде номограмм (рис. 10.2). Из рисунка видно, что с ростом температуры величина
. Такие зависимости и построены в виде номограмм (рис. 10.2). Из рисунка видно, что с ростом температуры величина 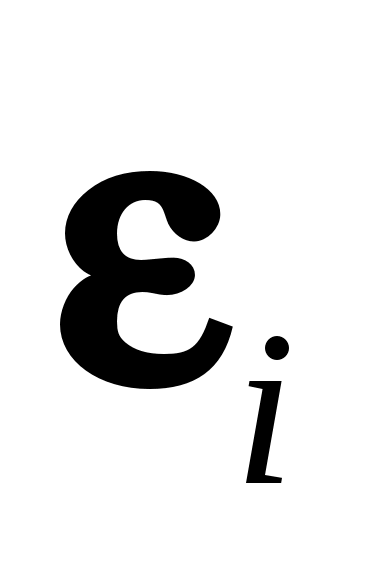 , как правило, снижается. Такой характер кривых связан с особенностями построения номограмм. Все кривые получены при условии
, как правило, снижается. Такой характер кривых связан с особенностями построения номограмм. Все кривые получены при условии 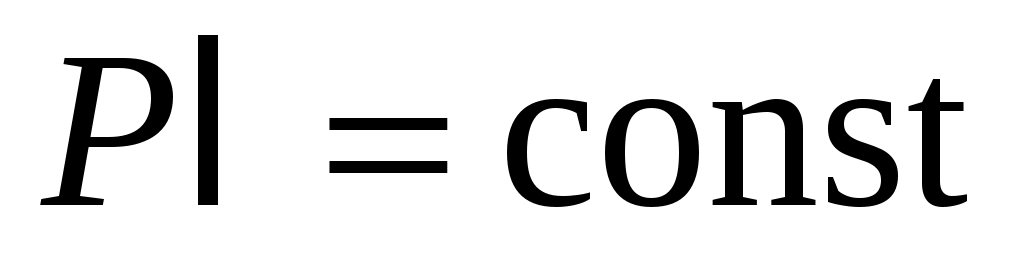 . Поэтому с ростом температуры, чтобы произведение
. Поэтому с ростом температуры, чтобы произведение 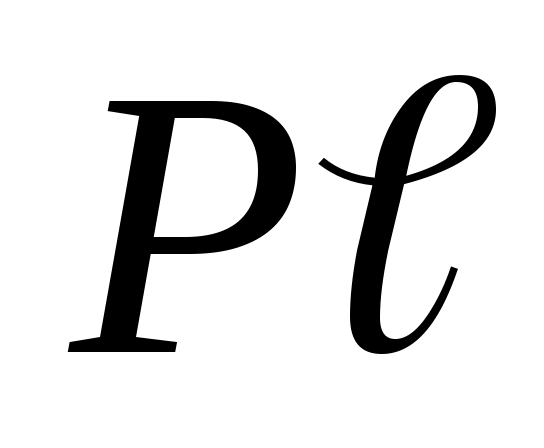 сохранялось неизменным, необходимо снижать концентрацию частиц. А поскольку объемное излучение пропорционально концентрации компонента, то это и приводит к уменьшению
сохранялось неизменным, необходимо снижать концентрацию частиц. А поскольку объемное излучение пропорционально концентрации компонента, то это и приводит к уменьшению 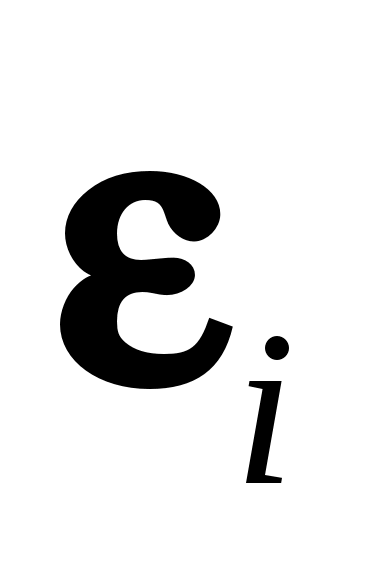 .
.
Предположение о том, что давление газа и величина
9.3.3 Теплообмен излучением между двумя телами, произвольно
расположенными в пространстве
Р
 ассмотрим тело 1 и тело 2, произвольно расположенные в пространстве. Очевидно, что в теплообмене будут участвовать лишь поверхности
ассмотрим тело 1 и тело 2, произвольно расположенные в пространстве. Очевидно, что в теплообмене будут участвовать лишь поверхности Отсюда
. Применяя метод сальдо Рис. 9.6
и законы Стефана-Больцмана и Кирхгофа, можно получить следующее выражение для результирующего потока излучением, записанное в стандартной форме:
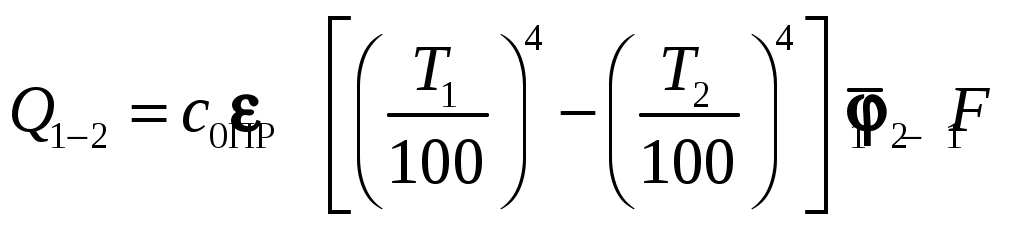 (9.22)
(9.22)или
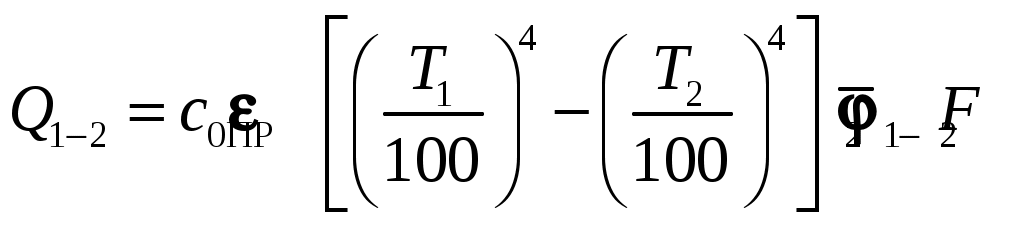 , (9.23)
, (9.23)где
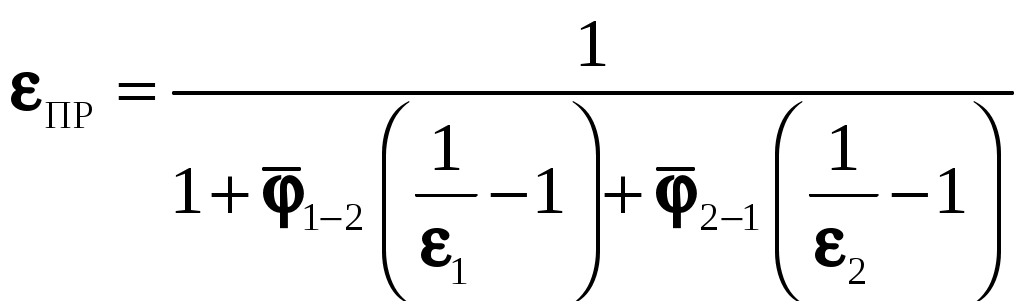 (9.24)
(9.24)Из полученных формул следует, что для расчета теплообмена излучением в общем случае необходимо знать угловые коэффициенты излучения. Рассмотрим их более подробно.
9.3.4. Геометрические свойства угловых коэффициентов излучения
Угловые коэффициенты излучения, если среда прозрачная, зависят только от геометрических свойств системы, а именно размеров тел, расстояния между ними и ориентации их в пространстве. Они обладают следующими свойствами.
1. Свойство взаимности
Из уравнений (9.22) и (9.23) можно видеть, что
Здесь
2. Свойство замыкаемости (замкнутости) тел
Рассмотрим замкнутую систему, состоящую из n тел. Пусть для первого тела эффективное излучение равно
, тогда
3. Свойство затеняемости
Рассмотрим два тела (рис. 9.7), между которыми размещено третье непрозрачное тело такое, что перегораживает все лучи с первого тела на второе и обратно. Тогда получаем:
Рис. 9.7
9.3.5. Методы определения угловых коэффициентов излучения
Существуют различные методы определения угловых коэффициентов излучения, среди которых сравнительно простым и достаточно эффективным является метод поточной алгебры.
 В этом случае рассматривают замкнутую систему, состоящую из трех невогнутых тел: 1, 2 и 3 (рис. 9.8). Для них известны поверхности
В этом случае рассматривают замкнутую систему, состоящую из трех невогнутых тел: 1, 2 и 3 (рис. 9.8). Для них известны поверхности Рис. 9.8 лении оси z велики по сравнению с их поперечными размерами, что позволяет пренебречь излучением с торцов, и используя свойства замыкаемости и взаимности, можно получить
10. ОБЪЕМНОЕ ИЗЛУЧЕНИЕ
Газы и пары обладают низкими коэффициентами поглощения, поэтому в излучении и поглощении участвуют все частицы (молекулы, атомы) газового объема. Такое излучение и называется объемным. Кроме того, для них характерно выборочное или селективное излучение и поглощение.
10.1. Особенности излучения газов и паров
В инженерной практике с излучением газов и паров встречаются в металлургических печах и топках паровых котлов, в которых теплота выделяется при сжигании органических топлив: твердых (при камерном сжигании угля), жидких (например, мазута) и газообразных (природного или искусственного газов). Во всех случаях при полном сжигании образуется углекислый газ (СО2), а при неполном – угарный газ (СО). Для сжигания топлива используется кислород воздуха, который подводится всегда с некоторым избытком. Поэтому в топке содержится О2 и, естественно, азот N2. В атмосферном воздухе всегда есть влага, поэтому в топочной смеси присутствует водяной пар (Н2О). Кроме того, влага может поступать в топку вместе с топливом. При сжигании природного газа возможно присутствие СН4. Иногда вместе с топливом попадают оксиды серы, фосфора и др. В общем случае в топочных газах могут находиться и твердые частицы угольной пыли и золы. Здесь рассмотрим излучение газового объема, не содержащего твердых частиц.
Исследования показали, что излучение и поглощение двухатомных газов (О2, N2) невелико, поэтому их излучение не учитывается. Излучение таких газов, как CO, CH4, S2O3 и др., значительно, но концентрация их мала, поэтому оно тоже не принимается во внимание. Таким образом, в инженерной практике учитывается лишь излучение CO2 и H2O.
Оба газа обладают выборочным излучением. Спектры излучения и поглощения их хорошо изучены. При этом различают тонкую и грубую структуру спектра. В расчетной практике учитывается лишь грубая структура, т.е. самые широкие полосы спектра. С увеличением температуры ширина полос излучения и поглощения увеличивается, что приводит к возрастанию излучательной и поглощательной способностей этих газов. Так как ширина полос для паров воды несколько больше, чем для углекислого газа, то и излучение их больше. Кроме того, излучение и поглощение обоих газов зависит от количества частиц в рассматриваемом объеме, которое определяется парциальным давлением каждого газа, и размерами газового объема, характеризуемого средней длиной пути луча
Следовательно, излучение каждого газа зависит от его природы, температуры, парциального давления P и размера
Экспериментально получено, что
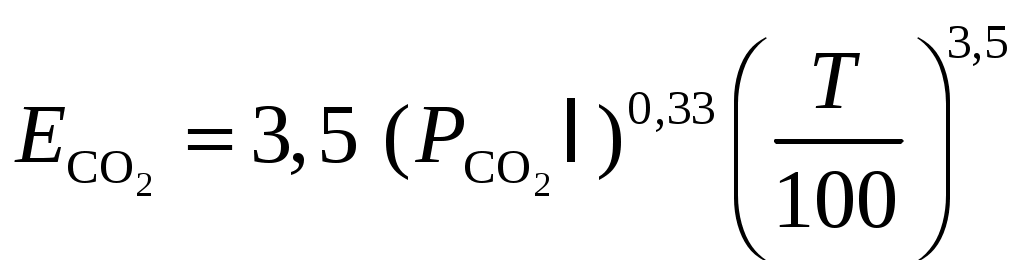 ,
, 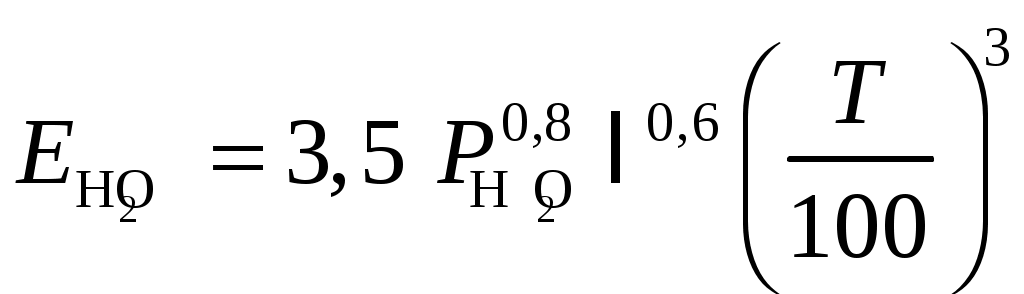 . (10.1)
. (10.1)Можно видеть, что в обоих случаях излучение газов не подчиняется закону Стéфана-Больцмана. Но обычно газ участвует в теплообмене со стенками топки, экранированной трубами, излучение которых подчиняется закону Стефана-Больцмана. Применение различных законов резко бы усложнило расчеты. Поэтому предполагают, что и излучение газов подчиняется закону четвертой степени, следовательно
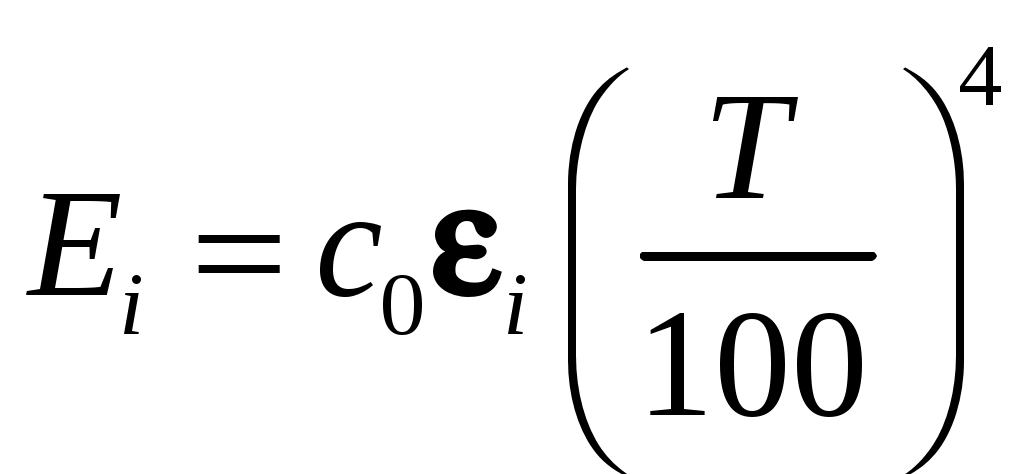 , а все отличие учитывается соответствующим выбором
, а все отличие учитывается соответствующим выбором Предположение о том, что давление газа и величина

