Файл: 1 дріс. Метрология лшеулер бірлігін амтамасыз етуді Мемлекеттік жйесіні ылыми негізі (МЖ).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 84
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Кездейсоқ шаманы таралудың теңестірілген заңы салыстырмалы түрде жиі кездеседі, оның сызбасы 3.2 суретте берілген.
W( 0 | |
3.2 сурет – Таралудың теңестірілген заңының сызбасы
Таралудің теңестірілген заңының ықтималды тығыздығының формуласы
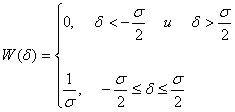. (3.3)Өлшенетін шаманың мәндері кейбір шекаралық шектерде әртүрлі, бірақ тең ықтималды болуы мүмкін.
Таралудың басқа заңдары МЕСТ 8.011 – 72 “өлшеулер дәлдігінің” көрсеткіштері және өлшеулер нәтижесін ұсыну формалары.
3.1.1 Таралу заңдарының негізгі сипаттамалары.
Бірқатар бақылаулардың математикалық тосу (МТ) – жекелеген бақылаулардың нәтижелерінің соған қатысты салыстырмалы шашырайтын шамасы.
Егер жүйелік қателіктер болмаса және жекелеген өлшемдердің нәтижелерінің шашырауы тек қана кездейсоқ қателіктермен шартталса, онда мұндай бақылау қатарының математикалық тосу өлшенетін шаманың нақты мәні болады.
Егер , онда мұндай бақылау қатарының математикалық тосу өлшенетін шаманың нақты мәнінен жүйелік қателік мәніне ойысатын болады.
Бірқатар бақылаудың дисперсиясы математикалық тосу айналасындағы жекелеген бақылаулардың нәтижелерінің шашырау дәрежесін көрсетеді. Дисперсия қаншалықты аз болса, соншалықты жекелеген нәтижелер шашырауы аз, соншалықты өлшеулер дәл орындалған болады. Сөйтіп, дисперсия жүргізілген өлшеулердің дәлдігі сипатында қызмет етеді.
Байқаулар қатарының орташа квадраттық ауытқуы
. Дисперсияны өлшеу бірлігі өлшенетін шаманың квадраты болып табылатындықтан, дәлдігін бағалау үшін орташа квадраттық ауытқу деп аталатын және дисперсиядан квадраттық түбіріне тең шама пайдаланылады.
3.1.2 Бірқатар бақылаудың негізгі сипаттамаларының бағалары.
Ықтималдық теориясы бойынша математикалық тосуынің бағасы жекелеген бақылаулар нәтижелерінің арифметикалық ортасы - болып табылатыны белгілі
, (3.4)
мұнда - i-й бақылау нәтижесі;
- бақылау нәтижелерінің саны.
бақылау қатарының шашырау бағасы келесі формула бойынша есептеледі
. (3.5)
бақылау қатарының орташа квадраттық аутқуы бақылау нәтижелерінің кездейсоқ қателіктерінің мөлшерінің негізгі сипаттамасы болып табылады.
Орташа квадраттық ауытқу бағасын есептеу формуласы
+ , (3.6)
n болғанда (нақтысында n > 30), S2 Д, S .
Тақырып бойынша қосымша ақпаратты [1-7,10] алуға болады.
4 дәріс. Өлшеулер қателігі (жалғасы)
Дәрістің мазмұны: дәл және техникалық өлшеулерде қателіктерді бағалау мен есептеу, таралу және кездейсоқ аксиомалары; байқаулар қатарының негізінде өлшеулер нәтижесінің қателіктерін ықтималдылық бағалау, өлшеу құралдардың және өлшеулердің дәлдігін арттыру әдістері.
Дәрістің мақсаты: байқаулар қатарының негізінде өлшеулер нәтижесінің қателіктерін ықтималдылық бағалауын игеру: сенімділік шекаралары, сенімділік интервалы және сенімділік ықтималдылығы; өлшеулердің кездейсоқ және жүйелік қателіктерін азайту әдістері, ӨҚ дәлдігін арттыру әдістері.
4.1 Дәл өлшеулер қателіктерін бағалау және есептеу
Дәл өлшеулер жүйелік қателіктер бола алмайтындай жүргізілуі қажет. Кездейсоқ қателіктер теориясы, тәжірибе деректеріне негізделген, екі аксиомаға тіректенеді.
Кездейсоқ аксиомасы: өлшеулердің саны өте үлкен болса, онда біркелкі жиі кездесетін кездейсоқ қателіктердің шамасы тең, бірақ таңбасы әртүрлі болады: теріс қателіктер саны оң қателіктер санына тең болады.
Таралу аксиомасы: шағын қателіктер үлкенге қарағанда жиірек болады, өте үлкен қателіктер кездеспейді.
Кездейсоқ шаманың, сондай-ақ кездейсоқ қателігінің толық жазбасы таралу заңы болып табылады. Кездейсоқ шаманың таралудың әртүрлі заңдары бар. Өлшеу тәжірибесінде кездейсоқ қателіктерді таралудің ең көбірек таралған заңдары қалыпты және бірқалыпты заңдары болып табылады.
4.1.1 Бірқатар байқаулар негізіндегі өлшеулер нәтижесі қателігінің ықтималдылық бағалары.
Бақылау нәтижелерін өңдеудің мақсаты - өлшенетін шаманың шындық мәнінің орнына қабылдануы мүмкін болатын шаманы және нақты мәнінің шындыққа жақын дәрежесін анықтау.
Нақты мәнінде қайтсе де кездейсоқ қателігі болады. Сондықтан нақты мәннің шындық мәнге жуық дәрежесін ықтималдылық теориясы тұрғысынан қарастыруға болады. Мұндай бағалау болатындай сенімділік интервалын алады. Кездейсоқ қателіктің сенімділік интервалы – берілген сенімділік ықтималмен кездейсоқ қателігінің мәндері түсетін интервал. Егер кездейсоқ қателігінің таралу заңы және осы заңның сипаттамалары белгілі болса, сенімділік интервалын айқындауға болады (3 дәріс).
8.011 – 72 МЕСТ-ке сәйкес сенімділік интервалы өлшеулер дәлдігін білдіретін негізгі формалардың бірі. МЕСТ өлшеу нәтижесін ұсынудың келесі формасын тағайындайды
, (4.1)
мұнда – өлшеу нәтижесі (орташа арифметикалық мәні);
, т, ж – өлшеудің абсолют қателігі мен төменгі және жоғарғы шекаралары;
Р – қателік осы шекараларда болатын сенімділік ықтималдығы.
Ықтималдылық теориясында дәлелдеткен - кездейсоқ қателіктің таралу заңы қалыпты болса, онда шама , бұл МТ = 0 және Д = 1 қалыпты заңы бойынша таралған кездейсоқ шамасы; ал бұл Стьюдент заңы бойынша таралған кездейсоқ шамасы. және үшін кесте бар , ол бойынша сәйкесті және үшін т, ж сенімділік интервалының шекарасын Р сенімділік ықтималдығымен анықтайтын мәндерін табуға болады.
, S -де, яғни бақылау санының артуы мен Стьюдент таралу заңы қалыптыға жуықтайды (тәжірибелік түрде n > 30 - -ға теңеседі).
Өлшеу тәжірибесінде сенімділік ықтималдықтың әртүрлі мәндерін қолданады: Р = 0,90; 0,95; 0,98; 0,99; 0,9973 және 0,999.
Қалыпты заңда кездейсоқ қателікті таралуда көбіне сенімділік ықтималдылығы 0,9973 болатын +3 дан -3 -дейінгі сенімділік интервалын пайдаланады. Бұл сенімділік ықтималдығы 370 кездейсоқ қателіктен орташа алғанда тек біреуі ғана = 3 мәнінен асатын болады. Тәжірибеде жекелеген өлшеулердің саны бірнеше ондағаннан үлкен болуы сирек кездеседі, мұнда
«3 сигма заңын» қолданады: қалыпты заң бойынша таралған барлық мүмкін болатын өлшеулердің кездейсоқ қателіктері практикалық тұрғыда 3абсолют мәнінен артпайды.
Орындалған өлшеулердің талдауының ең соңғы мақсаты қателіктер мен ықтималдықтың салыстырмалы жиілігінің өлшеуінің соңғылық нәтижесі үшін қабылданатын олардың орта арифметикалық мәнінің қателіктері өлшенетін шаманың бірқатар мәндерінің бақылау нәтижесінің қателігін анықтаудан тұрады.
4.1.1.1 Бақылау нәтижесінің қателігін (дәлдігін) бағалау.
Бақылау нәтижесінің дәлдігінің бағалауын - бақылаудың нәтижесінің орта квадраттық ауытқуы көрсетеді (3 дәріс). Бақылау нәтижесінің кездейсоқ ауытқуының бағасының дәлдігі және сенімділігі туралы толық түсінік алу үшін сенімділік шекаралары, сенімділік интервалы және сенімділік ықтималдығы көрсетілуі қажет. белгілі болса, сенімділік шекаралары мына түрде көрсетіледі: төменгі шекарасы (- ), жоғарғы шекарасы (+ ) (қысқаша ), бұл шектерден тыс Р=0,683 (немесе 68,3%) ықтималдықпен кездейсоқ ауытқулар мәндері ( ) аспайды. Сенімділік интервалы түрінде өрнектеледі. Өлшеу мақсатына байланысты басқа да сенім шекаралары берілуі мүмкін, ал бақылау нәтижесінің қателігінің сенімділік интервалы
, (4.2)
мұнда, - бақылау нәтижесінің орта квадраттық ауытқуы (3.6);
- квантиль көбейткіш, мұның мәні кездейсоқ қателіктің таралу заңына байланысты болады.
Сөйтіп, таралудің бірқалыпты заңы үшін және ол сенімділік ықтималдығына тәуелді емес. Таралудің қалыпты заңы үшін сенімділік ықтималдығы (Р) мәніне және бақылау мәндерінің (n) санына тәуелді: n > 30 – = ; n < 30 - = (Стьюдент заңы). Ең көп қолданылатын сенімділік ықтималдықтары Р және әртүрлі n үшін мәндері [8,П1-4-1 кесте] келтірілген.
4.1.1.2 Өлшеу нәтижесінің қателігін (дәлдігін) бағалау.
Өлшеу нәтижесі арифметикалық орташа мәніне тең деп алынады. Қателіктер теориясына сәйкес, өлшеу нәтижесінің орташа квадраттық ауытқу бағасы бақылаулардың нәтижесінің орташа квадраттық ауытқу бағасынан есе аз
. (4.3)
Өлшеу нәтижесінің қателігінің сенімділік интервалы
, (4.4)
мұнда, - квантиль көбейткіш;
- өлшеу нәтижесінің орташа квадраттық ауытқуы.