Восточно-Сибирский государственный университет технологии и управления.

Кафедра ЭСППиСХ


Допущен к защите

Руководитель проекта:

Кривошеин М.Ю.

“___”___________2020 г.


КУРСОВОЙ ПРОЕКТ

по курсу: Основы алгоритмизации энергетических задач.

на тему: Изучение метода Жордана с полным выбором ведущего элемента.

Студент 2 курса,

гр.ЗБ-639-2: Андриевский Я.А.

Улан-Удэ

2020

Восточно-Сибирский государственный университет технологий и управления

Кафедра ЭСПП и СХ
“Утверждаю”

Зав. кафедрой

____________________

“___”___________2020 г.

Задание

по курсовому проектированию

Студенту 2 курса ЗБ-639-2 группы Электротехнического факультета

Фамилия Андриевский Имя Ян Отчество Андреевич

Срок выполнения проекта__________________ 2020 г.

Защита проекта назначена на__________________ 2021 г.

Время выдачи задания__________________ 2020 г.

1. 
   Тема проекта
   

Изучение метода Жордана с полным выбором ведущего элемента.

2. 
   Задание и содержание расчетно-пояснительной записки
   

Введение

Изучение метода Жордана с полным выбором ведущего элемента. Вместо приведения матрицы А к треугольному виду можно попытаться сделать ее диагональной. На k-м шаге, имея ненулевой главный элемент, можно исключить все элементы (кроме диагонального) k-го столбца матрицы А. Вычисления аналогичны вычислениям по методу Гаусса; также допускается перестановка строк и столбцов и на n-1 шаге решается система линейных уравнений с диагональной матрицей.

Цель темы состоит в оценке этого метода. Взяв за основу алгоритм Дулиттла А1.4 [11] (метод LU-разложения), необходимо выполнить следующие задания.

1. Дать детальное описание алгоритма Жордана, с полным выбором ведущего элемента. Показать, как сохранить все множители для последующего применения при обработке правой части. r

2. Составить программу решения Ах=b с использованием этого алгоритма.

3. Завершить тему выполнением всех заданий темы 1.


Список использованной литературы.

Сборник алгоритмов решения систем линейных уравнений. Методические указания к практическим занятиям, курсовому проектированию и СРС.ВСГТУ, Улан-Удэ 2012 год

---

Руководитель проекта: Кривошеин М.Ю.

Задание принял к исполнению «___»______________2020г. ____________

(дата и подпись студента)



РАСЧЕТНО - ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Основной раздел

1. Теоретические аспекты численных методов

В данной курсовой работе рассматривается алгоритм решения системы линейных уравнений методом Жордана с полным выбором ведущего элемента.

Метод Жордана – разновидность метода Гаусса для решения системы линейных уравнений, в которой вместо приведения к треугольному виду матрица коэффициентов преобразуется в диагональную.

Полный выбор ведущего элемента - на k-м этапе в качестве ведущего выбирают максимальный по модулю элемент среди элементов матрицы, расположенных ниже и правее ведущего элемента и осуществляют соответствующую перестановку строк и столбцов.

Постановка задачи и описание алгоритма:

Задача состоит в решении системы уравнений , где A – матрица порядка n, – вектор, состоящий из n компонент:

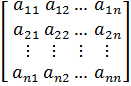A = , b =

Мы будем использовать расширенную матрицу A^* , в которой вектор является n + 1 столбцом:

A^* =

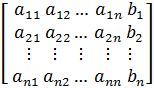
Наглядно метод Жордана можно представить в виде умножения матрицы A^* на матрицы L_k (k – текущая итерация алгоритма) справа n раз:

L_k = 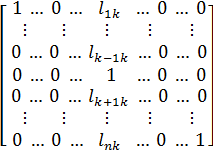, где l_ik= , 1

(в скобках указывается количество изменений элемента)

---

L_n(L_n-1 (L_n-2 … (L₁ = .

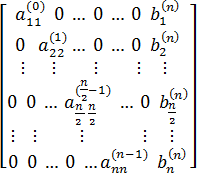Простым преобразованием = , = , получим:



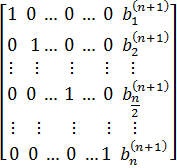
Искомые решения:

Пример: найдем решения системы .

Матрица A = , b = . Расширенная матрица = .

Вычислим L₁ : l₂₁ = , L₁ = ; L₁ =

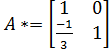
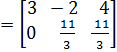. Теперь найдем L₂ : l₁₂ = =

---

, L₂ = ;

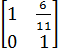L₂(L₁ = .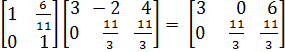

Приведем часть A матрицы к единичному виду:

и получим

Проверка: – верно.

В процессе нахождения диагональной матрицы может возникнуть ситуация, когда ведущий элемент равен нулю. Чтобы избежать этого, проводится выбор ведущего элемента – максимального ненулевого среди всех элементов матрицы, расположенных ниже и правее ведущего элемента и, если найденный ведущий элемент не совпадает с текущим, осуществляется соответствующая перестановка строк и столбцов.

Заметим, что при перестановке столбцов изменяется порядок переменных в уравнениях. Чтобы вывести корректный ответ, необходимо завести строку длины n и заполнить ее числами от 1 до n последовательно. При перестановке столбцов меняются местами элементы этой строки, с индексами, равными номерам столбцов соответственно.

Теперь рассмотрим реализацию алгоритма метода Жордана на ЭВМ. Она будет отличаться от наглядной, так как нерационально хранить и вычислять матрицы L_k . Мы также используем расширенную матрицу A^* , а все вычисления сводятся к двум операциям:

1. Умножение строки на множитель

2. Сложение одной строки с алгебраическим дополнением к другой (вычитание строк)

Каждая итерация k состоит из трех частей:

1. Выбор ведущего элемента. Строку и столбец, содержащие ведущий элемент назовем ведущими. Если необходимо, переставляем строки и столбцы.

2. Все элементы ведущей строки расширенной матрицы делим на направляющий элемент. В результате получаем направляющую строку с ведущим элементом, равным единице.

3. Из каждой строки, кроме k-ой, поэлементно вычитаем элементы ведущей строки, умноженные на элемент, лежащий на пересечении ведущего столбца и текущей строки.

---

После итерации все элементы ведущего столбца равны нулю, кроме ведущего, который равен единице. Продолжаем преобразовывать матрицу, пока возможно выбрать ведущий элемент. Процесс заканчивается в двух случаях: когда ниже ведущей строки и правее ведущего столбца нет элементов, либо когда все они равны нулю.

Допустим, процесс прервался на s-ой итерации. Первые s строк, начиная с единицы, содержат единицу в k-ом столбце и значение k-ой переменной в столбце n + 1. Если есть строки с номерами > s, то они должны быть нулевыми, иначе система уравнений неразрешима. Это необходимо проверять. Переменные с индексами i, , называются базисными, переменные с индексами i, (если s = n, то таких переменных нет), называются небазисными и выражаются через другие, указывать в ответе их не будем.

Также стоит отметить, что на ЭМВ существует предел точности вычислений, он ограничен размером типа. В представленной реализации коэффициенты хранятся в типе Real, что обеспечивает точность до 11-12 цифр после запятой. Во многих задачах такая точность не требуется, поэтому точность можно искусственно ограничить, используя сравнение с заданным граничным значением, меньше которого любое число приравнивается к нулю. Это используется для предотвращения возникновения чисел больших порядков, так как в программе присутствует деление.

2. Программная реализация

Итак, учитывая все вышесказанное, для программной реализации метода Жордана нам необходимо:

• 
  Считывать матрицу порядка n и вектор из n компонент и записывать их в расширенную матрицу.
  
• 
  Выбирать ведущий элемент
  
• 
  Исключать все, кроме ведущего, элементы столбца при помощи умножения строки на число и вычитания строк
  
• 
  Проверять систему уравнений на разрешимость
  
• 
  Выводить ответ в виде s строк с переменной и ее значением
  

Выделим для выбора ведущего элемента и исключения столбца отдельные подпрограммы (процедуру и функцию).

Реализация на псевдокоде:

Необходимые переменные: n – количество строк, j – номер ведущей строки (столбца), A[0… n

---

Смотрите также файлы

• Правила транспортировки закупаемых материальных ресурсов и погрузочноразгрузочных работ. Транспортировка закупаемых материальных ресурсов.doc

• Изучение вращательного.docx

• Обзор суммативного оценивания за 3 четверть.docx

• Как хорошо, что есть семья, которая от бед любых везде хранит меня.docx

• Исходные данные Установленный лимит остатка денежных средств в кассе 5000 рублей. Остаток в кассе на начало дня 2000 рублей. Получены в кассу денежные средства с расчетного счета для выдачи зарплаты работникам 100000 рублей и на хозяйственные нужды 3000 р.docx