Файл: Изучение метода Жордана с полным выбором ведущего элемента.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 35
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 1 … n + 1] – расширенная матрица коэффициентов c нулевым столбцом, отвечающим за порядок переменных, i, k – итераторы, s – количество успешных итераций
function LeadElementSelection – выбор ведущего элемента
Функция принимает на вход j, n, A и определяет переменные leadingString – номер новой ведущей строки, leadingColumn – номер нового ведущего столбца, max – модуль максимального значения, выбирает ведущий элемент, изменяя матрицу А, и возвращает “true” или “false” в зависимости от того, удалось ли сделать выбор
Начало
max присвоить значение модуля A[j, j]
leadingString присвоить значение j
leadingColumn присвоить значение j
(Нахождение максимального по модулю элемента ниже ведущей строки и правее ведущего столбца)
Для строк i от j до n:
Для столбцов k от j до n:
Если A[i, k] не равно 0 и A[i, k] больше максимума, то:
max присвоить значение модуля A[i, k]
leadingString присвоить значение i
leadingColumn присвоить значение k
Конец цикла
Конец цикла
(изменение порядка строк и столбцов, если необходимо)
Если ведущий элемент не A[j, j], то:
 Если leadingString не равно j, то поменять местами строку j с leadingString поэлементно
Если leadingString не равно j, то поменять местами строку j с leadingString поэлементно
Если leadingColumn не равен j, то поменять местами столбец j с leadingColumn местами поэлементно
Если max равен нулю, то вернуть значение “false”, иначе вернуть “true”
Конец функции
procedure ColumnElimination – исключение не ведущих элементов столбца
Процедура принимает на вход j, n, A и исключает все элементы j-того столбца кроме ведущего (A[j, j]), изменяя матрицу А.
Начало
(получаем направляющую строку с ведущим элементом, равным единице)
Для столбцов k от n + 1 до j:
A[j, k] присвоить значение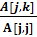
Конец цикла
(исключаем не ведущие элементы ведущего столбца)
Для строк i от 1 до n:
Если номер строки i равен j, то перейти к следующей итерации
Иначе для столбцов k от n + 1 до j:
A[i, k] присвоить значение (A[i, k] - A[j, k]
*A[i, j]);
Конец цикла
Конец цикла
Конец процедуры
program JordansMethod – основная часть программы:
Начало
Присвоить числу успешных итераций s значение 0
 Считать n (размер матрицы коэффициентов, число уравнений в системе)
Считать n (размер матрицы коэффициентов, число уравнений в системе)
Считать расширенную матрицу системы уравнений в A, заполнить нулевую строку числами от 0 до n последовательно
(применяем метод Жордана)
Для j от 1 до n:
Если функция LeadElementSelection(j, n, A) вернула “false”, то завершить цикл
Иначе:
Увеличить количество успешных итераций s на единицу
Вызвать процедуру ColumnElimination(j, n, A)
Конец цикла
(проверяем систему на разрешимость и выводим ответ)
Если число успешных итераций s не равно числу строк n, то:
Для строк i от s + 1 до n:
Если A[i, n + 1] равно 0, то:
(показываем, что система неразрешима)
s присвоить значение 0 (показываем, что система неразрешима)
Выходим из цикла
Конец цикла
Если s равно 0, то выводим: “Unsolvable system”
Иначе для i от 1 до s:
Вывести: “x”, A[0, i], “ = “, A[i, n + 1]
Перейти на новую строку
Конец цикла
Конец программы
 Пример 1: решим систему линейных уравнений
Пример 1: решим систему линейных уравнений 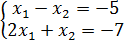 , используя представленную выше программную реализацию
, используя представленную выше программную реализацию
Вызывается program JordansMethod.
1. Считываем n, n = 2. Считываем и заполняем матрицу А, получаем
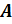 =
= 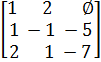 , где
, где 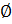 - неиспользуемая ячейка памяти. Не забываем, что индекс первой строки в матрице А равен 0.
- неиспользуемая ячейка памяти. Не забываем, что индекс первой строки в матрице А равен 0.
2. Начинаем выполнение алгоритма с первого входа в функцию
LeadElementSelection с параметрами j = 1, n = 2,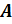 =
= 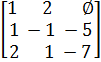 :
:
Изначально max = 1, leadingString
= 1, leadingColumn = 1.
После выбора максимального элемента получаем:
max = 2, leadingString = 2, leadingColumn = 1.
Необходимо поменять местами строки 1 и 2: =
= 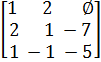 .
.
Функция возвращает “true”, так как выбор прошел успешно (A[1, 2] не
равно нулю).
3. Число успешных итераций s равно 1. Вызываем процедуру
ColumnElimination с параметрами j = 1, n = 2, =
= 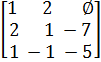 :
:
Получаем ведущую строку с ведущим элементом, равным единице –
 =
= 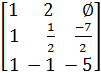 и вычитаем ее, умноженную на A[2, 1] =
и вычитаем ее, умноженную на A[2, 1] = 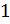 , из второй строки, чтобы A[2, 1] стало
, из второй строки, чтобы A[2, 1] стало
 равным 0:
равным 0:  =
= 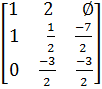 .
.
4. Переходим на следующую итерацию, теперь попробуем исключить
не ведущие элементы из второго столбца. Вызываем LeadElementSelection с параметрами j = 2, n = 2,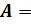
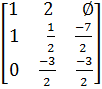 :
:
Изначально max = , leadingString = 2, leadingColumn = 2.
, leadingString = 2, leadingColumn = 2.
После выбора максимального элемента получаем:
max = , leadingString = 2, leadingColumn = 2. Так как leadingString = = leadingColumn = j, то строки и столбцы переставлять не нужно.
, leadingString = 2, leadingColumn = 2. Так как leadingString = = leadingColumn = j, то строки и столбцы переставлять не нужно.
Выбор ведущего элемента прошел успешно, возвращаем “true”.
5. Число успешных итераций s равно 2. Вызываем процедуру
ColumnElimination с параметрами j = 2, n = 2,
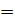
 :
:
Получаем ведущую строку с ведущим элементом, равным единице –
 =
= 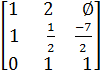 и вычитаем ее, умноженную на A[1, 2] =
и вычитаем ее, умноженную на A[1, 2] =  , из первой строки, чтобы A[1, 2] стало равным 0:
, из первой строки, чтобы A[1, 2] стало равным 0:  =
= 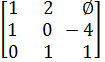 .
.
6. Цикл завершился, делаем проверку на разрешимость: s равно n,
проверка не нужна, переходим к выводу ответа. При выборе ведущих элементов столбцы не переставлялись, поэтому переменные идут по порядку:
x1 = -4
x2 = 1
Программа завершена

Пример 2 : Попробуем найти решения системы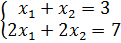 .
.
n = 2, =
= 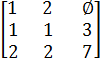
После первой итерации получим: s =1, =
= 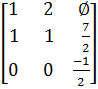 .
.
Переходим ко второй итерации. Вызываем функцию LeadElementSelection с параметрами j = 2, n = 2,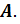 max =
max = 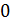 , leadingString = 2, leadingColumn = 2. После поиска главного элемента max все еще равно 0, а значит выбор главного элемента прошел неудачно. Функция возвращает “false”
, leadingString = 2, leadingColumn = 2. После поиска главного элемента max все еще равно 0, а значит выбор главного элемента прошел неудачно. Функция возвращает “false”
Проверяем систему на разрешимость, так как s не равно n, проверяя строки от s + 1 до n на равенство последнего элемента в строке нулю. В данном случае во второй строке последний элемент не равен нулю, то есть:
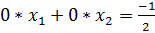 – неверное равенство, следовательно система неразрешима. Выводим ответ “Unsolvable system”. Программа завершена.
– неверное равенство, следовательно система неразрешима. Выводим ответ “Unsolvable system”. Программа завершена.
Подробнее о программной реализации.
Основные параметры программы регулируются константами:
MaxMatrixSize – отвечает за выделение памяти на двумерный массив (расширенную матрицу коэффициентов). Под хранение матрицы отводится (MaxMatrixSize + 1) * (MaxMatrixSize + 1) * 6 байт (хранятся значения типа Real). По умолчанию равен 50.
NumberLength – количество символов в числе во время вывода. Применяется для удобного отображения значений. По умолчанию равно 10.
Accuracy – видимая точность вычислений, количество цифр после запятой в числе во время вывода. Число округляется , чтобы соответствовать точности.
По умолчанию равна 4.
 NullLimit – реальная точность вычислений, значение по модулю ведущего элемента ниже этой границы приравнивается к нулю. Используется для избежания деления на ноль, когда число настолько маленькое, что не входит в тип Real, а так же для избежания значений большого порядка, так как в программе производятся деления на значение ведущего элемента.
NullLimit – реальная точность вычислений, значение по модулю ведущего элемента ниже этой границы приравнивается к нулю. Используется для избежания деления на ноль, когда число настолько маленькое, что не входит в тип Real, а так же для избежания значений большого порядка, так как в программе производятся деления на значение ведущего элемента.
Ввод
На вход сначала подается размер матрицы коэффициентов (не расширенной) равный количеству переменных в системе (будем считать, что в системе из n переменных n уравнений, то есть мы можем составить матрицу коэффициентов n*n (если переменной нет в уравнении, то ее коэффициент равен нулю) ).
Затем вводится расширенная матрица коэффициентов, состоящая из n строк по n + 1 элементов, где n + 1 столбец – столбец правых частей уравнения.
Для выхода из программы нужно нажать клавишу “Enter”.
Так выглядит результат работы программы:
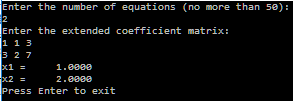
Или так:
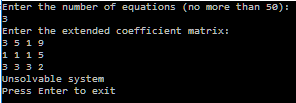
Исходный код программы прилагается в файле JordansMethod.pas. Также прилагаются JordansMethod.exe – работающая версия программы и ReadMe.txt – руководство по использованию программы.

3. Вычислительные эксперименты
Временная сложность алгоритма
Оценим сложности подпрограмм: LeadElementSelection =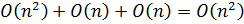
function LeadElementSelection – выбор ведущего элемента
Функция принимает на вход j, n, A и определяет переменные leadingString – номер новой ведущей строки, leadingColumn – номер нового ведущего столбца, max – модуль максимального значения, выбирает ведущий элемент, изменяя матрицу А, и возвращает “true” или “false” в зависимости от того, удалось ли сделать выбор
Начало
max присвоить значение модуля A[j, j]
leadingString присвоить значение j
leadingColumn присвоить значение j
(Нахождение максимального по модулю элемента ниже ведущей строки и правее ведущего столбца)
Для строк i от j до n:
Для столбцов k от j до n:
Если A[i, k] не равно 0 и A[i, k] больше максимума, то:
max присвоить значение модуля A[i, k]
leadingString присвоить значение i
leadingColumn присвоить значение k
Конец цикла
Конец цикла
(изменение порядка строк и столбцов, если необходимо)
Если ведущий элемент не A[j, j], то:
 Если leadingString не равно j, то поменять местами строку j с leadingString поэлементно
Если leadingString не равно j, то поменять местами строку j с leadingString поэлементноЕсли leadingColumn не равен j, то поменять местами столбец j с leadingColumn местами поэлементно
Если max равен нулю, то вернуть значение “false”, иначе вернуть “true”
Конец функции
procedure ColumnElimination – исключение не ведущих элементов столбца
Процедура принимает на вход j, n, A и исключает все элементы j-того столбца кроме ведущего (A[j, j]), изменяя матрицу А.
Начало
(получаем направляющую строку с ведущим элементом, равным единице)
Для столбцов k от n + 1 до j:
A[j, k] присвоить значение
Конец цикла
(исключаем не ведущие элементы ведущего столбца)
Для строк i от 1 до n:
Если номер строки i равен j, то перейти к следующей итерации
Иначе для столбцов k от n + 1 до j:
A[i, k] присвоить значение (A[i, k] - A[j, k]
*A[i, j]);
Конец цикла
Конец цикла
Конец процедуры
program JordansMethod – основная часть программы:
Начало
Присвоить числу успешных итераций s значение 0
 Считать n (размер матрицы коэффициентов, число уравнений в системе)
Считать n (размер матрицы коэффициентов, число уравнений в системе)Считать расширенную матрицу системы уравнений в A, заполнить нулевую строку числами от 0 до n последовательно
(применяем метод Жордана)
Для j от 1 до n:
Если функция LeadElementSelection(j, n, A) вернула “false”, то завершить цикл
Иначе:
Увеличить количество успешных итераций s на единицу
Вызвать процедуру ColumnElimination(j, n, A)
Конец цикла
(проверяем систему на разрешимость и выводим ответ)
Если число успешных итераций s не равно числу строк n, то:
Для строк i от s + 1 до n:
Если A[i, n + 1] равно 0, то:
(показываем, что система неразрешима)
s присвоить значение 0 (показываем, что система неразрешима)
Выходим из цикла
Конец цикла
Если s равно 0, то выводим: “Unsolvable system”
Иначе для i от 1 до s:
Вывести: “x”, A[0, i], “ = “, A[i, n + 1]
Перейти на новую строку
Конец цикла
Конец программы
 Пример 1: решим систему линейных уравнений
Пример 1: решим систему линейных уравнений Вызывается program JordansMethod.
1. Считываем n, n = 2. Считываем и заполняем матрицу А, получаем
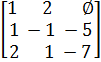 , где
, где 2. Начинаем выполнение алгоритма с первого входа в функцию
LeadElementSelection с параметрами j = 1, n = 2,
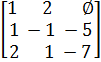 :
:Изначально max = 1, leadingString
= 1, leadingColumn = 1.
После выбора максимального элемента получаем:
max = 2, leadingString = 2, leadingColumn = 1.
Необходимо поменять местами строки 1 и 2:
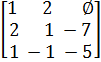 .
.Функция возвращает “true”, так как выбор прошел успешно (A[1, 2] не
равно нулю).
3. Число успешных итераций s равно 1. Вызываем процедуру
ColumnElimination с параметрами j = 1, n = 2,
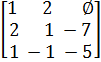 :
:Получаем ведущую строку с ведущим элементом, равным единице –
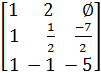 и вычитаем ее, умноженную на A[2, 1] =
и вычитаем ее, умноженную на A[2, 1] =  равным 0:
равным 0: 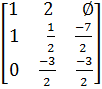 .
. 4. Переходим на следующую итерацию, теперь попробуем исключить
не ведущие элементы из второго столбца. Вызываем LeadElementSelection с параметрами j = 2, n = 2,
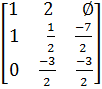 :
:Изначально max =
После выбора максимального элемента получаем:
max =
Выбор ведущего элемента прошел успешно, возвращаем “true”.
5. Число успешных итераций s равно 2. Вызываем процедуру
ColumnElimination с параметрами j = 2, n = 2,
 :
:Получаем ведущую строку с ведущим элементом, равным единице –
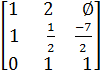 и вычитаем ее, умноженную на A[1, 2] =
и вычитаем ее, умноженную на A[1, 2] = 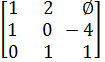 .
. 6. Цикл завершился, делаем проверку на разрешимость: s равно n,
проверка не нужна, переходим к выводу ответа. При выборе ведущих элементов столбцы не переставлялись, поэтому переменные идут по порядку:
x1 = -4
x2 = 1
Программа завершена

Пример 2 : Попробуем найти решения системы
n = 2,
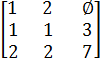
После первой итерации получим: s =1,
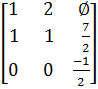 .
. Переходим ко второй итерации. Вызываем функцию LeadElementSelection с параметрами j = 2, n = 2,
Проверяем систему на разрешимость, так как s не равно n, проверяя строки от s + 1 до n на равенство последнего элемента в строке нулю. В данном случае во второй строке последний элемент не равен нулю, то есть:
Подробнее о программной реализации.
Основные параметры программы регулируются константами:
MaxMatrixSize – отвечает за выделение памяти на двумерный массив (расширенную матрицу коэффициентов). Под хранение матрицы отводится (MaxMatrixSize + 1) * (MaxMatrixSize + 1) * 6 байт (хранятся значения типа Real). По умолчанию равен 50.
NumberLength – количество символов в числе во время вывода. Применяется для удобного отображения значений. По умолчанию равно 10.
Accuracy – видимая точность вычислений, количество цифр после запятой в числе во время вывода. Число округляется , чтобы соответствовать точности.
По умолчанию равна 4.
 NullLimit – реальная точность вычислений, значение по модулю ведущего элемента ниже этой границы приравнивается к нулю. Используется для избежания деления на ноль, когда число настолько маленькое, что не входит в тип Real, а так же для избежания значений большого порядка, так как в программе производятся деления на значение ведущего элемента.
NullLimit – реальная точность вычислений, значение по модулю ведущего элемента ниже этой границы приравнивается к нулю. Используется для избежания деления на ноль, когда число настолько маленькое, что не входит в тип Real, а так же для избежания значений большого порядка, так как в программе производятся деления на значение ведущего элемента. Ввод
На вход сначала подается размер матрицы коэффициентов (не расширенной) равный количеству переменных в системе (будем считать, что в системе из n переменных n уравнений, то есть мы можем составить матрицу коэффициентов n*n (если переменной нет в уравнении, то ее коэффициент равен нулю) ).
Затем вводится расширенная матрица коэффициентов, состоящая из n строк по n + 1 элементов, где n + 1 столбец – столбец правых частей уравнения.
Для выхода из программы нужно нажать клавишу “Enter”.
Так выглядит результат работы программы:

Или так:

Исходный код программы прилагается в файле JordansMethod.pas. Также прилагаются JordansMethod.exe – работающая версия программы и ReadMe.txt – руководство по использованию программы.

3. Вычислительные эксперименты
Временная сложность алгоритма
Оценим сложности подпрограмм: LeadElementSelection =

