Файл: Изучение метода Жордана с полным выбором ведущего элемента.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 36
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. ColumnElimination = 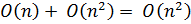 .
.
Теперь оценим сложность главной функции:
program JordansMethod =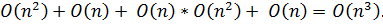 Это грубая оценка, потому что количество итераций в циклах зависит не только от n, но и от j, которое принимает значения от 1 до n.
Это грубая оценка, потому что количество итераций в циклах зависит не только от n, но и от j, которое принимает значения от 1 до n.
Чтобы более точно определить сложность, посчитаем количество операций. Мы рассматриваем случай, когда система из n уравнений имеет n решений, то есть алгоритм не обрывается. Тогда выполняется: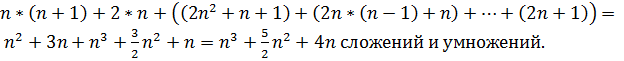 Это совпадает с полученной оценкой временной сложности алгоритма.
Это совпадает с полученной оценкой временной сложности алгоритма.
Объемная сложность алгоритма
В главной функции используются следующие переменные и структуры данных: Matrix (массив значений типа Real размера (n+1)*(n+1) ) и n, i, j, s типа Integer. Это занимает ((n+1)*(n+1)*6 + 4*2) байт. Теперь найдем наибольший объем памяти, занимаемый локальными переменными вызываемых процедур и функций, он равен (2*6 + 4 * 2) байт (в функции LeadElementSelection). Тогда максимальный объем занимаемой памяти: (n+1)*(n+1)*6 + 4*2 + 2*6 + 4 * 2 =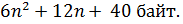 Зависимость объема занимаемой памяти от размера матрицы:
Зависимость объема занимаемой памяти от размера матрицы: 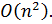
Оценка сложности выполнения программы
Предложенная функция GetTime считает время с точностью до сотых секунды – такой точности не достаточно, поэтому здесь используется функция QueryPerformanceCounter из модуля Windows, чтобы замерять время выполнения в микросекундах. Сначала определяем тактовую частоту процессора с помощью QueryPerformanceFrequency, затем с помощью двух вызовов функции QueryPerformanceCounter до и после блока с алгоритмом находим количество тактов процессора, делим их разность на количество тактов в микросекунду – это и есть искомое время работы алгоритма. При этом программа строит случайную матрицу заданного порядка и выводит время в микросекундах. (В качестве генератора случайных чисел используется функция Random, так как предлагаемая в методическом пособии функция Urand не работает).
выполнения в микросекундах. Сначала определяем тактовую частоту процессора с помощью QueryPerformanceFrequency, затем с помощью двух вызовов функции QueryPerformanceCounter до и после блока с алгоритмом находим количество тактов процессора, делим их разность на количество тактов в микросекунду – это и есть искомое время работы алгоритма. При этом программа строит случайную матрицу заданного порядка и выводит время в микросекундах. (В качестве генератора случайных чисел используется функция Random, так как предлагаемая в методическом пособии функция Urand не работает).
Результаты вычислений с некоторыми порядками:




И характеристический профиль:
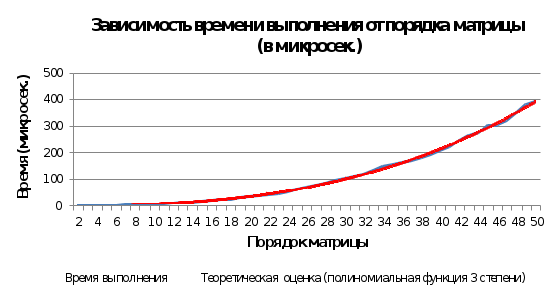
 Как мы видим, результаты эксперимента совпали с вычисленной ранее временной сложностью алгоритма (
Как мы видим, результаты эксперимента совпали с вычисленной ранее временной сложностью алгоритма (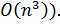
Оценка точности вычисления программы для хорошо обусловленных матриц
Хорошо обусловленные матрицы можно создать с помощью заполнения матрицы коэффициентов случайными числами. В качестве решения системы уравнений мы предполагаем 1, 1, …, 1 – все переменные равны 1. Исходя из этого, мы строим правые части системы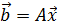 . Относительную погрешность вычислений рассматриваем как максимальную разность между полученным значением и единицей по отношению к полученному значению. Для этого изменим код программы, чтобы создавать матрицу таким образом и получать на выходе погрешность вычислений.
. Относительную погрешность вычислений рассматриваем как максимальную разность между полученным значением и единицей по отношению к полученному значению. Для этого изменим код программы, чтобы создавать матрицу таким образом и получать на выходе погрешность вычислений.
Полученные значения имеют вид:
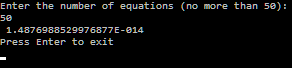
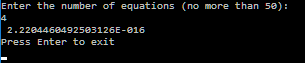
Относительная погрешность измерения зависит от порядка матрицы и ее числа обусловленности. При числе обусловленности близком к единице погрешность близка к нулю. Рассматривая средние значения измерений погрешности (по 30 измерений (результат мало отличается от 100 и более измерений) для каждой нормы, что сводит влияние чисел обусловленности к минимуму) получаем ответы вида:

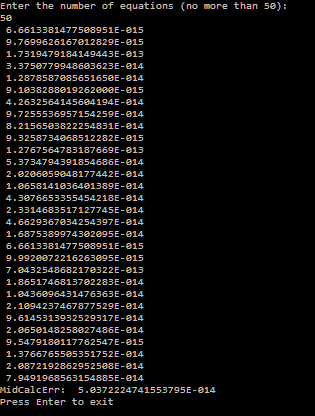
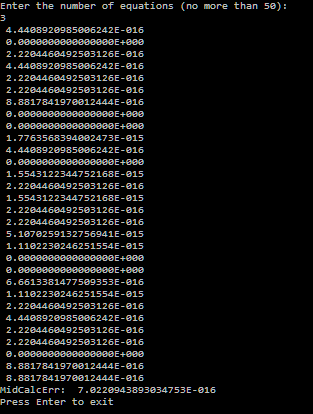
Как видно из примеров, при разном порядке матрицы относительная погрешность различна, значит между этими величинами существует зависимость. Проведя подобные вычисления для всех порядков от 2 до 50, получим:
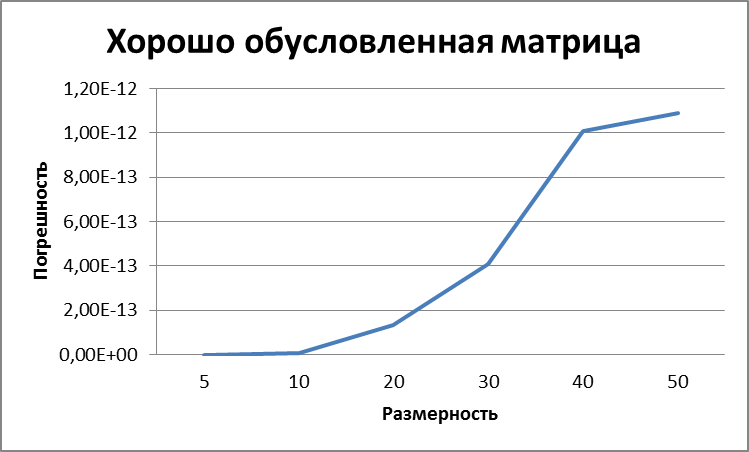
Как мы видим, функция зависимости относительной погрешности от порядка матрицы близка к квадратичной функции: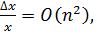 где n –порядок матрицы.
где n –порядок матрицы.
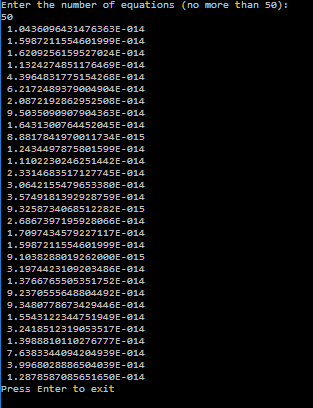
 Теперь найдем зависимость относительной погрешности от числа обусловленности матрицы. Для этого проведем 30 измерений погрешности при зафиксированном порядке матрицы (пусть n равно 50).
Теперь найдем зависимость относительной погрешности от числа обусловленности матрицы. Для этого проведем 30 измерений погрешности при зафиксированном порядке матрицы (пусть n равно 50).
Полученные значения имеют вид:
Зависимость относительной погрешности от числа обусловленности (для упрощения мы находим зависимость, не вычисляя числа обусловленности) :
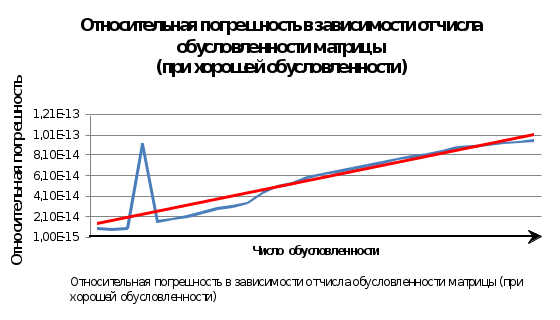
Линия тренда показывает, что зависимость относительной погрешности от чисел обусловленности близка к линейной.
Это значит, что при хорошей обусловленности матрицы относительная погрешность сильнее зависит от порядка матрицы, чем от числа обусловленности.
 Оценка точности вычисления программы для плохо обусловленных матриц
Оценка точности вычисления программы для плохо обусловленных матриц
В качестве плохо обусловленной матрицы будем использовать матрицу Гильберта ( A[i, j] = 1/(i + j - 1) ). Перепишем программу, чтобы она создавала матрицы Гильберта порядка n и выводила относительную погрешность для системы уравнений с такой матрицей. Получаем:
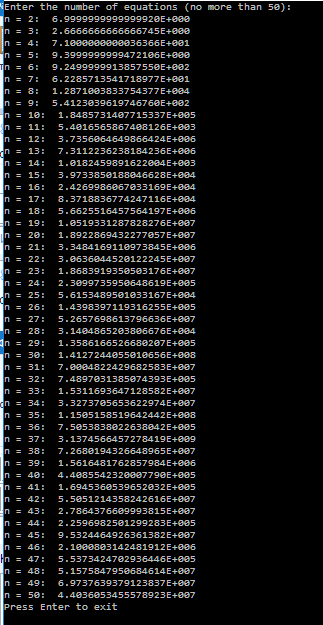
В виде характеристического профиля:

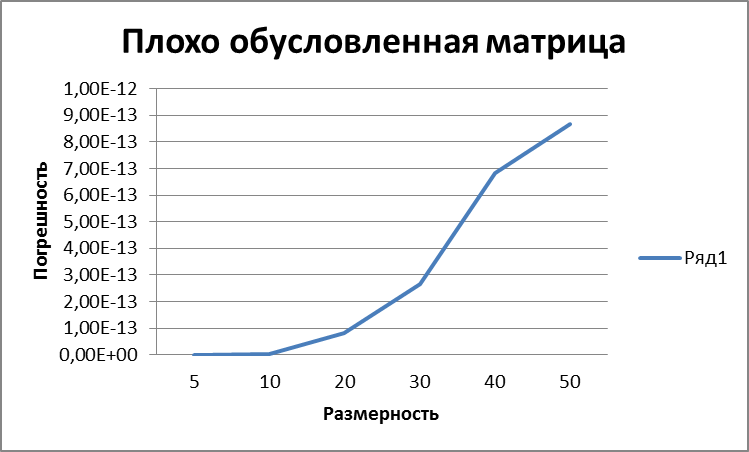
Явной зависимости не наблюдается, что характерно для плохо обусловленных матриц. Стоит отметить, что относительная погрешность вычислений с плохо обусловленной матрицей больше чем с хорошо обусловленной матрицей на величину от 13 до 24(!) порядков, что говорит об огромной погрешности в вычислениях с плохо обусловленной матрицей.
Теперь рассмотрим поведение ведущих элементов в плохо обусловленной системе, для этого перепишем программу, чтобы она выводила только ведущие элементы. Получим:
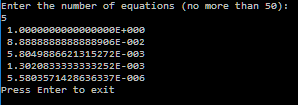
Как мы видим, порядок ведущего элемента уменьшается поитерационно. Это сильно влияет на точность измерений, так как в алгоритме используется деление элементов строки на ведущий элемент. С увеличением порядка матрицы степень минимального ведущего элемента уменьшается. Таким образом, в матрице порядка 50 степень минимально ведущего элемента равна -19. Отобразим это на характеристическом профиле:

 Сравним поведение ведущих элементов плохо обусловленной матрицы с ведущими элементами хорошо обусловленной матрицы:
Сравним поведение ведущих элементов плохо обусловленной матрицы с ведущими элементами хорошо обусловленной матрицы:
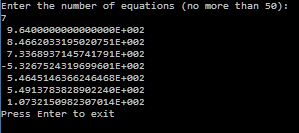
Порядок ведущих элементов в хорошо обусловленной матрице почти не меняется (в зависимости от порядка матрицы, чем больше порядок, тем сильнее различаются ведущие элементы).
Таким образом, в плохо обусловленной матрице в отличие от хорошо обусловленной ведущий элемент постоянно уменьшается и может сильно отличаться от предыдущих. Поэтому при расчетах с плохо обусловленной матрицей такая огромная относительная погрешность.
Подробнее о программной реализации
В данном подразделе изменялся функционал программы JordansMethod, поэтому мы вынесли это в отдельный файл - JordansMethodResearch. Так как получение программы, предназначенной для изучения систем линейных уравнений, не было целью работы, то полученный код с функционалом для измерения времени выполнения, подсчета относительной погрешности и т.д. представлен в рабочем состоянии, но без инструкций и объяснений. В зависимости от цели раскомментируйте необходимые блоки кода.
получение программы, предназначенной для изучения систем линейных уравнений, не было целью работы, то полученный код с функционалом для измерения времени выполнения, подсчета относительной погрешности и т.д. представлен в рабочем состоянии, но без инструкций и объяснений. В зависимости от цели раскомментируйте необходимые блоки кода.
Список используемой литературы
1. Электрические системы. Математические задачи электроэнергетики/ Под ред. В.А. Веникова. Т.1 - М.: Высшая школа, 2011. - 334с.
2. Курбацкий В.Г., Томин Н.В. Математические задачи электроэнергетики Ч.1: учеб. пособие для вузов/ Курбацкий В.Г. и др.- ГОУ ВПО «БрГУ», 2009.-142с.
3.Давыдов В.В., Борисов Г.О. Программирование матричных вычислений в электротехнических задачах. Сборник алгоритмов
решения систем линейных уравнений. Улан-Удэ, 1997.
4.Райс Дж. Матричные вычисления и математическое обеспечение. - М.: Мир, 1984. - 246 с

Теперь оценим сложность главной функции:
program JordansMethod =
Чтобы более точно определить сложность, посчитаем количество операций. Мы рассматриваем случай, когда система из n уравнений имеет n решений, то есть алгоритм не обрывается. Тогда выполняется:
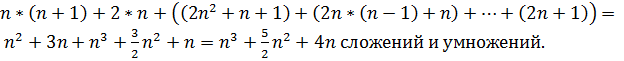 Это совпадает с полученной оценкой временной сложности алгоритма.
Это совпадает с полученной оценкой временной сложности алгоритма. Объемная сложность алгоритма
В главной функции используются следующие переменные и структуры данных: Matrix (массив значений типа Real размера (n+1)*(n+1) ) и n, i, j, s типа Integer. Это занимает ((n+1)*(n+1)*6 + 4*2) байт. Теперь найдем наибольший объем памяти, занимаемый локальными переменными вызываемых процедур и функций, он равен (2*6 + 4 * 2) байт (в функции LeadElementSelection). Тогда максимальный объем занимаемой памяти: (n+1)*(n+1)*6 + 4*2 + 2*6 + 4 * 2 =
Оценка сложности выполнения программы
Предложенная функция GetTime считает время с точностью до сотых секунды – такой точности не достаточно, поэтому здесь используется функция QueryPerformanceCounter из модуля Windows, чтобы замерять время
 выполнения в микросекундах. Сначала определяем тактовую частоту процессора с помощью QueryPerformanceFrequency, затем с помощью двух вызовов функции QueryPerformanceCounter до и после блока с алгоритмом находим количество тактов процессора, делим их разность на количество тактов в микросекунду – это и есть искомое время работы алгоритма. При этом программа строит случайную матрицу заданного порядка и выводит время в микросекундах. (В качестве генератора случайных чисел используется функция Random, так как предлагаемая в методическом пособии функция Urand не работает).
выполнения в микросекундах. Сначала определяем тактовую частоту процессора с помощью QueryPerformanceFrequency, затем с помощью двух вызовов функции QueryPerformanceCounter до и после блока с алгоритмом находим количество тактов процессора, делим их разность на количество тактов в микросекунду – это и есть искомое время работы алгоритма. При этом программа строит случайную матрицу заданного порядка и выводит время в микросекундах. (В качестве генератора случайных чисел используется функция Random, так как предлагаемая в методическом пособии функция Urand не работает).Результаты вычислений с некоторыми порядками:




И характеристический профиль:

 Как мы видим, результаты эксперимента совпали с вычисленной ранее временной сложностью алгоритма (
Как мы видим, результаты эксперимента совпали с вычисленной ранее временной сложностью алгоритма (Оценка точности вычисления программы для хорошо обусловленных матриц
Хорошо обусловленные матрицы можно создать с помощью заполнения матрицы коэффициентов случайными числами. В качестве решения системы уравнений мы предполагаем 1, 1, …, 1 – все переменные равны 1. Исходя из этого, мы строим правые части системы
Полученные значения имеют вид:


Относительная погрешность измерения зависит от порядка матрицы и ее числа обусловленности. При числе обусловленности близком к единице погрешность близка к нулю. Рассматривая средние значения измерений погрешности (по 30 измерений (результат мало отличается от 100 и более измерений) для каждой нормы, что сводит влияние чисел обусловленности к минимуму) получаем ответы вида:



Как видно из примеров, при разном порядке матрицы относительная погрешность различна, значит между этими величинами существует зависимость. Проведя подобные вычисления для всех порядков от 2 до 50, получим:

Как мы видим, функция зависимости относительной погрешности от порядка матрицы близка к квадратичной функции:
 Теперь найдем зависимость относительной погрешности от числа обусловленности матрицы. Для этого проведем 30 измерений погрешности при зафиксированном порядке матрицы (пусть n равно 50).
Теперь найдем зависимость относительной погрешности от числа обусловленности матрицы. Для этого проведем 30 измерений погрешности при зафиксированном порядке матрицы (пусть n равно 50).Полученные значения имеют вид:

Зависимость относительной погрешности от числа обусловленности (для упрощения мы находим зависимость, не вычисляя числа обусловленности) :

Линия тренда показывает, что зависимость относительной погрешности от чисел обусловленности близка к линейной.
Это значит, что при хорошей обусловленности матрицы относительная погрешность сильнее зависит от порядка матрицы, чем от числа обусловленности.
 Оценка точности вычисления программы для плохо обусловленных матриц
Оценка точности вычисления программы для плохо обусловленных матриц В качестве плохо обусловленной матрицы будем использовать матрицу Гильберта ( A[i, j] = 1/(i + j - 1) ). Перепишем программу, чтобы она создавала матрицы Гильберта порядка n и выводила относительную погрешность для системы уравнений с такой матрицей. Получаем:

В виде характеристического профиля:


Явной зависимости не наблюдается, что характерно для плохо обусловленных матриц. Стоит отметить, что относительная погрешность вычислений с плохо обусловленной матрицей больше чем с хорошо обусловленной матрицей на величину от 13 до 24(!) порядков, что говорит об огромной погрешности в вычислениях с плохо обусловленной матрицей.
Теперь рассмотрим поведение ведущих элементов в плохо обусловленной системе, для этого перепишем программу, чтобы она выводила только ведущие элементы. Получим:

Как мы видим, порядок ведущего элемента уменьшается поитерационно. Это сильно влияет на точность измерений, так как в алгоритме используется деление элементов строки на ведущий элемент. С увеличением порядка матрицы степень минимального ведущего элемента уменьшается. Таким образом, в матрице порядка 50 степень минимально ведущего элемента равна -19. Отобразим это на характеристическом профиле:

 Сравним поведение ведущих элементов плохо обусловленной матрицы с ведущими элементами хорошо обусловленной матрицы:
Сравним поведение ведущих элементов плохо обусловленной матрицы с ведущими элементами хорошо обусловленной матрицы:
Порядок ведущих элементов в хорошо обусловленной матрице почти не меняется (в зависимости от порядка матрицы, чем больше порядок, тем сильнее различаются ведущие элементы).
Таким образом, в плохо обусловленной матрице в отличие от хорошо обусловленной ведущий элемент постоянно уменьшается и может сильно отличаться от предыдущих. Поэтому при расчетах с плохо обусловленной матрицей такая огромная относительная погрешность.
Подробнее о программной реализации
В данном подразделе изменялся функционал программы JordansMethod, поэтому мы вынесли это в отдельный файл - JordansMethodResearch. Так как
 получение программы, предназначенной для изучения систем линейных уравнений, не было целью работы, то полученный код с функционалом для измерения времени выполнения, подсчета относительной погрешности и т.д. представлен в рабочем состоянии, но без инструкций и объяснений. В зависимости от цели раскомментируйте необходимые блоки кода.
получение программы, предназначенной для изучения систем линейных уравнений, не было целью работы, то полученный код с функционалом для измерения времени выполнения, подсчета относительной погрешности и т.д. представлен в рабочем состоянии, но без инструкций и объяснений. В зависимости от цели раскомментируйте необходимые блоки кода.Список используемой литературы
1. Электрические системы. Математические задачи электроэнергетики/ Под ред. В.А. Веникова. Т.1 - М.: Высшая школа, 2011. - 334с.
2. Курбацкий В.Г., Томин Н.В. Математические задачи электроэнергетики Ч.1: учеб. пособие для вузов/ Курбацкий В.Г. и др.- ГОУ ВПО «БрГУ», 2009.-142с.
3.Давыдов В.В., Борисов Г.О. Программирование матричных вычислений в электротехнических задачах. Сборник алгоритмов
решения систем линейных уравнений. Улан-Удэ, 1997.
4.Райс Дж. Матричные вычисления и математическое обеспечение. - М.: Мир, 1984. - 246 с


