Файл: Парная линейная регрессия.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.02.2024

Просмотров: 15

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Тема: Парная линейная регрессия

Лабораторная №1



Имеются исходные данные (10 наблюдений):

Объем производства, млн. руб.
17
14
26
27
27
35
18
22
49
12

Численность рабочих, чел.
32
33
42
51
60
64
35
40
80
20,5



Необходимо определить, какой из заданных показателей является зависимой переменной, а какой – независимой. Построить поле корреляции. Найти точечные и интервальные оценки параметров модели 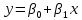. Оценить значимость коэффициентов регрессии, используя t-критерий Стьюдента и доверительные интервалы истинных значений параметров. Верифицировать полученную модель, используя дисперсионный анализ в регрессии и элементы теории корреляции. Интерпретировать полученные результаты. Сделать прогноз на основе модели.

Решение: 1 способ (ручной)


1 этап: Спецификация модели.
Определим, какой из заданных показателей будет зависимой переменной, а какой независимой. Так как труд является одним из факторов производства (экономическая теория), то численность работников обозначим в качестве независимой переменной 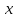, а объем производства – .

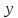Чтобы определить характер зависимости, построим поле корреляции:


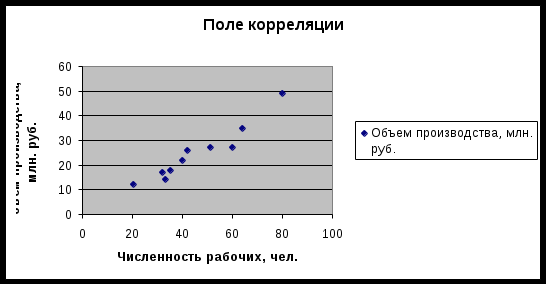
Следующим шагом наносим на поле корреляции прямую
:


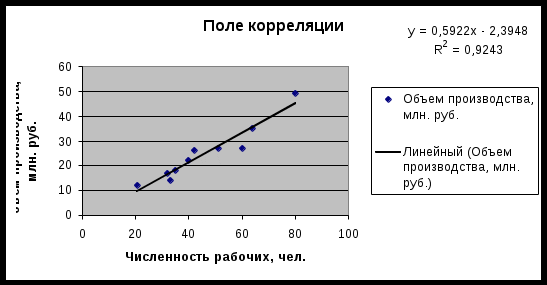
Из графика видно, что точки распределены практически однородно относительно прямой, поэтому можно сказать, что условие гомоскедастичности выполняется.
2 этап: Построение модели.
Найдем оценки параметров модели помощью метода наименьших квадратов (МНК). Оценки параметров модели находятся из условия: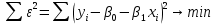

.

Тогда:

,

,

,

.

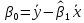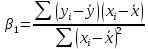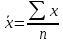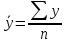Построим вспомогательную таблицу для расчетов:

№ наблюдения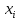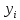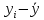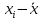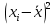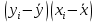












1
32
17
-7,7
-13,75
189,063
105,875

2
33
14
-10,7
-12,75
162,563
136,425

3
42
26
1,3
-3,75
14,0625
-4,875

4
51
27
2,3
5,25
27,5625
12,075

5
60
27
2,3
14,25
203,063
32,775

6
64
35
10,3
18,25
333,063
187,975

7
35
18
-6,7
-10,75
115,563
72,025

8
40
22
-2,7
-5,75
33,0625
15,525

9
80
49
24,3
34,25
1173,06
832,275

10
20,5
12
-12,7
-25,25
637,563
320,675

Итого
457,5
247
0
0
2888,625
1710,75


,

,

,

.

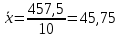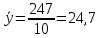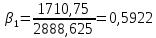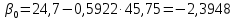Коэффициенты совпадают с уравнением на диаграмме.

При этом уравнение модели напишем в виде: .

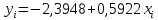Для анализа полученной модели рассчитываем теоретические значения объясняемой переменной: .

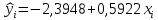Также найдем значение остатков: 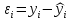и минимальное значение остаточной суммы квадратов 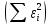. Для этого составим вспомогательную таблицу:


№ наблюдения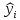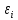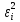








1
17
16,5567
0,4433
0,1965

2
14
17,1489
-3,1489
9,9156

3
26
22,4791
3,5209
12,3967

4
27
27,8092
-0,8092
0,6548

5
27
33,1394
-6,1394
37,6922

6
35
35,5083
-0,5083
0,2584

7
18
18,3335
-0,3335
0,1112

8
22
21,2946
0,7054
0,4976

9
49
44,9841
4,0159
16,1275

10
12
9,7460
2,254
5,0805

Итого
247
247
0
82,9309


Остаточная сумма квадратов:

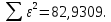
Вычислим несмещенные оценки дисперсий оценок:

,

.

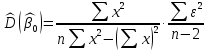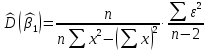Несмещенная оценка дисперсии ошибок наблюдений:

.

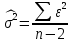Для расчетов составим вспомогательную таблицу:

№ наблюдения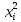




1
32
1024

2
33
1089

3
42
1764

4
51
2601

5
60
3600

6
64
4096

7
35
1225

8
40
1600

9
80
6400

10
20,5
420,25

Итого
457,5
23819,25

Таким образом, получаем:

,

.

.

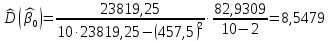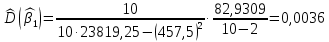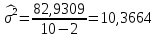3 этап: Оценка значимости коэффициентов регрессии
Оценка значимости коэффициентов регрессии при доверительной вероятности 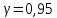с помощью:

а) доверительных интервалов истинных значений параметров.

Для нахождения интервальных оценок полученных коэффициентов регрессии предварительно вычислим квантиль распределения Стьюдента:

.

,

.

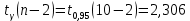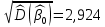
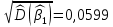Доверительный интервал для параметра :

,

.


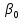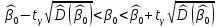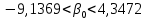Доверительный интервал для параметра :

,

.

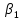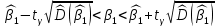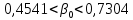Как мы видим, доверительный интервал для коэффициента регрессии 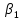не содержит нулевых значений, значит, коэффициент считается статистически значимым, доверительный интервал для параметра 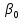содержит 0, соответственно, он считается незначимым.
б) t-критерий Стьюдента

Проверяем гипотезу 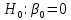против альтернативной гипотезы 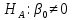, используя при этом статистику .

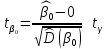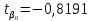– наблюдаемое или экспериментальное значение t-статистики.

Критическая область двухсторонняя:



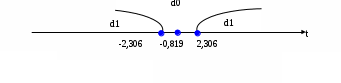
Гипотеза 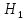отвергается с вероятностью 0,95, следовательно, принимается гипотеза 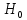, так как 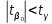, т. е. 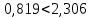. Это означает, что параметр 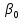незначим.

Проверяем гипотезу 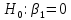против альтернативной гипотезы 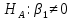, используя при этом статистику

Смотрите также файлы