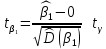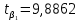.

– наблюдаемое или экспериментальное значение t-статистики.

Критическая область двухсторонняя:



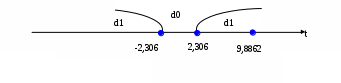
Гипотеза отвергается с вероятностью 0,95, следовательно, принимается гипотеза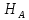 , так как 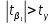, т. е. 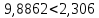. Это означает, что параметр – значим.
4 этап: Верификация модели
Пригодность построенной модели или ее верификация, а также качество оценивания регрессии может быть проверено двумя равноценными способами: дисперсионным анализом в регрессии и с использованием элементов теории корреляции.
а) Дисперсионный анализ в регрессии
Суть метода заключается в разложении общей суммарной дисперсии объема производства на составляющие, обусловленные действием численности работников, и остаточную дисперсию, обусловленную дисперсию, обусловленную ошибкой или всеми неучтенными в данной модели переменными.

Для проверки гипотезы о равенстве таких дисперсий используем критерий Фишера (F-критерий). Поскольку для оценок дисперсий используются суммы квадратов 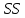отклонений значений данной переменной от ее средней величины, то можно говорить о разложении общей суммы квадратов 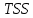на составляющие.

Cреднее значение 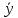зависимой переменной составляет 24,7 млн. (средний объем производства в течение наблюдаемого периода). Для расчета сумм квадратов составим вспомогательную таблицу:

№ наблюдения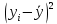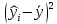
1	17	16,5567	59,29	66,3133
2	14	17,1489	114,49	57,0191
3	26	22,4791	1,69	4,9324
4	27	27,8092	5,29	9,6671
5	27	33,1394	5,29	71,2235
6	35	35,5083	106,09	116,8193
7	18	18,3335	44,89	40,5323
8	22	21,2946	7,29	11,5967
9	49	44,9841	590,49	411,4447
10	12	9,7460	161,29	223,6221
Итого	247	247	1096,10	1013,17

---

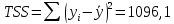– величина, характеризующая разброс значений относительно среднего значения .

Разобьем эту сумму на две части: объясненную регрессионным уравнением и необъясненную (т. е. связанную с ошибками :

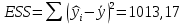– сумма квадратов, объясненная регрессией,

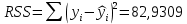– остаточная сумма квадратов, обусловленная ошибкой.

Проверка: 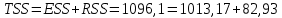(верно).

Найдем коэффициент детерминации:

.

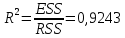Значение коэффициента детерминации близко к 1. Это означает, что 92,43 % общей вариации объема производства объясняется численностью работников.

При этом остальные 7,57 % приходятся на долю прочих факторов, не учтенных в уравнении регрессии.

К таким факторам можно отнести: объем основных и оборотных средств, спрос на продукцию, цену и т. д.

Далее при заданном уровне значимости 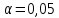проверяем гипотезу об отсутствии линейной функциональной связи между и , используя статистику критерия Фишера: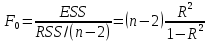

.

Число степеней свободы: .

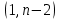Критическое значение: .

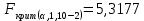Результаты представлены в таблице:
Дисперсионный анализ одномерной регрессии

Источник дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат 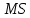1	Критерий Фишера	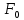Критическая точка	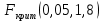Гипотеза
Регрессор x	1	1013,17	1013,17	97,7362	5,3177	Отклонить
Ошибка (остаток)	8	82,93	10,37
Общая дисперсия (итог)	9	1096,1

---

Критическая область правосторонняя:



Если при заданном уровне значимости наблюдаемое значение 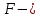статистики больше критической точки 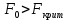, т.е. гипотеза отвергается, то есть линейная связь между и есть, и результаты наблюдений не противоречат предположению о ее линейности.

Полученную модель в целом можно считать пригодной для дальнейшего использования.
б) Использование элементов теории корреляции
Другой способ верификации линейной модели состоит в использовании элементов теории корреляции. Мерой линейной связи двух величин является коэффициент корреляции:

.
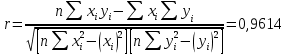Проверка: 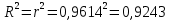(верно).

Значение коэффициента корреляции говорит о том, что линейная связь между численностью работников и объемом производства очень тесная и прямая, т.е. рост численности работников приводит к увеличению объема производства.

Проверяем гипотезу об отсутствии линейной связи между и 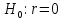с помощью критерия Стьюдента:

,

.

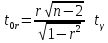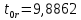Критическая область двухсторонняя:



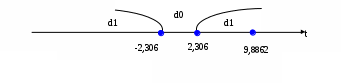
С вероятностью 0,95 гипотезу 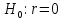отвергаем, так как 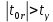, т. е.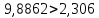

---

. Это означает, что коэффициент корреляции статистически значим.
5 этап: Интерпретация полученных показателей
Таким образом, коэффициент является незначимым. Значение коэффициента регрессии говорит о том, что при увеличении численности работников на 1 человека, объем продукции увеличится на 0,592 млн. руб. или 592,2 тыс. рублей.

Найдем коэффициент эластичности для данной модели:

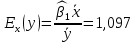(полученное выражено в процентах)

Значение коэффициента эластичности приближенно показывает, что значение величины объема производства изменится на 1,097 % при изменении численности работников на 1% от среднего значения.
6 этап: Прогноз на основе линейной модели
Точечный прогноз: .

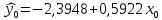Допустим, прогнозное значение независимой переменной изменяется на 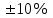от среднего значения. Тогда оптимистическое и пессимистическое значения 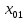и 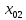составят:

.

.

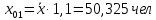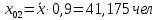При этом объем продукции в оптимистическом случае составит:

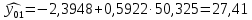млн. руб.,

в пессимистическом соответственно:

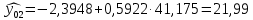млн. руб.

Интервальный прогноз значения :

.

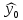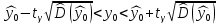Дисперсия величины 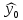определяется по формуле:

.

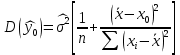Для исчисления дисперсии составим вспомогательную таблицу:

№ наблюдения
1	32	189,0625
2	33	162,5625
3	42	14,0625
4	51	27,5625
5	60	203,0625
6	64	333,0625
7	35	115,5625
8	40	33,0625
9	80	1173,0625
10	20,5	637,5625
Итого	457,5	2888,625

---

Необходимые для расчета значения:

,

,

,

.

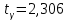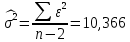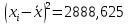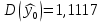Оптимистический интервальный прогноз при (численность работников увеличится на 10% от среднего уровня):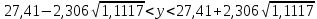

,

.

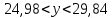Пессимистический интервальный прогноз при (численность работников снизится на 10% от среднего уровня):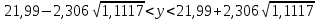

,

.
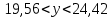Графически наши прогнозы можно представить так:


С вероятностью 0,95 можно гарантировать, что в случае увеличения численности работников на 10% от среднего значения, объем продукции составит от 24,98 млн. руб. до 29,84 млн. руб.; в случае снижения численности работников на 10% от среднего показателя, объем продукции составит от 19,56 млн. руб. до 24,42 млн. руб.

Решение: 2 способ (с помощью функции «анализ - регрессия» пакета анализа MS Excel)

Проверка всех результатов расчетов проводилась с использованием функции «анализ данных-регрессия» пакета анализа MS Excel.

Все расчеты, приведенные ранее, подтвердились.

ВЫВОД ИТОГОВ:
Регрессионная статистика
Множественный R	0,961426032
R-квадрат	0,924340015
Нормированный R-квадрат	0,914882516
Стандартная ошибка	3,219683797
Наблюдения	10

---

Смотрите также файлы

• Тема Основы рыночной экономики.pdf

• Деятельность педагогического коллектива в работе с детьми группы риска.docx

• Общие вопросы.doc

• Портал фнс россии.pdf

• Методические указания к лабораторным работам по дисциплине объектноориентированное программирование.doc