Файл: Модуль і. Основи інформаційних технологій в системі охорони здоров'Я. Обробка та аналіз медикобюлогічних даних.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 19.03.2024

Просмотров: 241

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

a b| Ф Щ :| J jhz yjШ& Р ис. 6. Панель інструментів Формы Поля формиПанель інструментів Фор.мы містить кнопки, призначені для вставлення полів, створення таблиць і рамок, засоби захисту форми, які дають змогу користувачам вводити дані тільки у відведені для цього поля. Призначення інструментів панелі інструментів Фор.мы відображено в табл. 1 14Таблиця І. Призначення інструментів панелі інструментів Формы

Рис. 17. Режим коиструктори для таблиці «Пацієнти»Зв'яжи між таблицями, які забезпечують посилальну цілісність даних, наглядно представлено на схемі даних (команда меню Сервис/Схема данных (рис. 18). 32i>] Microsoft Access - [Снема данных]

Access.

лі = 9. Обчислення критерію вірогідності коефіцієнта кореляції:t =10. Визначення стандартних значень критеріїв Ст'юдента відповідно трьомпрограмам вірогідності (95%, 99%, 99,9%) за допомогою таблиці для кількостіступенів свободи (див. вище) v=2n-2.11. Порівняння коефіцієнтів вірогідності коефіцієнта кореляціїстандартними значеннями критеріїв Ст'юдента. Висновок про вірогідністькоефіцієнта кореляції. 72В MS Excel для обчислення цього параметру існує вбудована функція КОРРЕЛ.Практичні завданнясЗь Завдання 1. Обчислення основних статистичних характеристик вибірок.Визначити середнє арифметичне, середнє квадратичне відхилення, помилку репрезентативності, моду та медіану результатів вимірювання швидкості кровотоку 10 пацієнтів до наркозу.

І1,844ег при х = 0 (уі>= 11.84 мг/л).

Рис. 62. Форма для списку лікарських засобівСтворена форма призначена насамперед для зручного введення інших записів (рядків) у цю таблицю даних (хоча можна і безпосередньо заповнювати таблицю). Щоб додати ще один запис до таблиці, використовують кнопку Добавить, після чого заповнюють усі поля для наступного запису. Якщо в списку є поля, які обчислюються програмою, вони також подаються у формі, але без відповідних полів введення даних. Для перегляду вже заповнених записів використовують кнопки Напад і Далее.Крім того форма дає змогу шукати записи за певними критеріями. Для цього потрібно клацнути на кнопці Критерии, після чого у правому верхньому куті форми з'являється напис Критерии. Якщо заповнити відповідні поля форми? кнопки Назад і Далее показуватимуть лише ті записи таблиці, що задовольняють введеним умовам. Для числових полів можна вводити математичні умови порівняння (=, <, >, о, <=, >=). У текстових полях можна використовувати символи шаблону (* - будь-яка кількість будь-яких дозволенних символів, ? -будь-який один довільний символ).З даними у списку в Excel можна здійснювати перетворення різного типу, зокрема, сортування та вибірку. На схемі 7 подано алгоритм виконання вказаних операцій. З детальним описом вказаних дій модна ознайомитися у Додатку. 127Сортування і вибіркаІ

Одне з найпростіших - сортування виконується за допомогою команди Сортировка пункту меню Данные. Програма автоматично розпізнає таблицю даних (коли активною є комірка всередині списку) і відкриває діалогове вікно Сортировка диапазона (рис. 76).Сортировка диапазонаСортироеать поЗ атем по ft' по убьів-afnw |Лк»оька фарна _^J t# по еоэрастетиюБ последнюю очереди по — |Показання до mcti_tJ & по еограстанио^ г» y6biMf*irt) Идентифицировать поля m'* подписям (первая строка диапазона)" обдзнщечняі* стогоцо* чиста гтарепетры...окJОтпнма Рис: 73. Діалогове вікно «Сортировки диапазона» 149Якщо перший рядок відформатований інакше або містить об'єкти, що відрізняються від об'єктів інших рядків, у діалоговому вікні пропонується здійснити сортування за назвами цих стовпців. В іншому разі Excel використовує безпосередні назви стовпців, наприклад ІСтол6еаА JJj |столбеие jj Змінити автоматичний вибір програми можна за допомогою поля Идентифицировать поля по. Діалогове вікно Сортировка диапазона дає змогу вибрати черговість сортування за стовпцями і напрям сортування кожного із стовпців. Якщо список треба відсортувати тільки за одним полем списку, слід зробити активною одну з комірок цього стовпця та скористатися відповідними кнопками панеліАІ ЯІінструментів Стандартная, за зростанням я+ або ж за спаданням At.Для сортування лише частини списку необхідно виділити потрібний діапазон комірок і виконати команду Сортировка. Якщо виділено не всі комірки рядків, то переміщування стосуватиметься лише виділених комірок, а в інших переміщувань не відбудеться, тобто записи (внутрішні зв'язки інформації) будуть зруйновані і список зіпсується. В Excel можливе сортування за встановленими в програмі списками (днітижня, місяці року тощо), а також за списками користувача, що створюються задопомогою вкладки Списки діалогового вікна Параметры, яке викликаєтьсяоднойменною командою пункту меню Сервис (рис. 77): Международные Сохранение Вид Вычислений ПравкаСписки:Параметры Орфография БезопасностьСписки Диаграмма Цр*т Проверка ошибде Общие ПереходЭлементы списка: M onday, Tuesday, Wednesday, Thursday, *. | Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, 5e January, February, March, April, May, Jum Пн, Єт, Cp, Чт, Пт, Сб, Єс Понедельник, Вторник, Среда, Четверг, янв, фее, мар, апр, май, ннэн, июл, авг. Январь, Февраль, Март, Апрель, Май, И Пн, Вв, Ср, Чт, Пт, Сб, Цд Понеділок, Вівторок, Середа, Четвер, П Січ, ГЬог, Бер, Кві, Тра, Чер, Лип, Сер, В , Лютий, Березе^, Квітень, ТравіN9. Нііва. Пікаоська *<49НазваЛікарська формаПоказання до застосуваннявиробникКількість упаковокЦіна, грнТермін придатностіДобавить Импорт списка из ячеек:Импорт O KОтмена Р ис. 74. Діалогове вікно «Параметры», вкладка «Списки»Список користувача можна ввести в поле Элементы списка в окремих рядках, а потім клацнути на кнопці Добавить. Якщо список уже міститься в певному діапазоні комірок робочого аркуша, достатньо ввести цей діапазон у поле Импорт списка из ячеек і клацнути на кнопці Импорт. Список користувача, що задає порядок сортування, потрібно вибрати у діалоговому вікні Параметры 150сортировки (кнопка Параметры діалогового вікна Сортировка диапазона) у полі Сортировка по перео.му ключу. Порядок сортування за списком користувача можна застосовувати тільки для сортування за першим параметром.Порядок корчування, що викорисювусться за замовчуванням,При сортуванні за зростанням Excel використовує наступний порядок: - Числа сортуються від найменшого від'ємного до найбільшого додатного числа.Ллфаеітно-цифрове сортування. При сортуванні алфавітно-цифрового тексту програма порівнює значення за знаками зліва направо. Наприклад, якщо комірка містить текст «А 100», Excel помістить її після комірки, що містить запис «А1», і перед коміркою, що містить запис «А1 \».Текст, що містить числа, сортується в наступному порядку: 0123456789 (пробіл) !"#$%&()*,./:;?@[\]Л_4{|}

Найти и заменить | Заменить Найти:- М еньше *Отмена П араметры поискаН аправление: Везде _" 5і»«тьвать регистрТолько слово целиком Подртановочные знаки Цмиїносится как Все словоформы НайтиФормат * Специальные тР ис. 77. Діалогове вікно Найти и іаменитьЗаміна тексту.Іноді може знадобитися замінити існуючий текст на новий. Для цього можна вибрати вкладку Заменить діалогового вікна Найти и заменить або вибрати відповідну команду у меню Правка. У вкладці Заменить слід ввести умови пошуку й заміни:у полі Найти - ввести фрагмент тексту, який необхідно замінити;- у полі Заменить на - ввести фрагмент тексту для заміни;— натиснути кнопку Найти далее; 159для заміни знайденого слова - натиснути кнопку Заменить, для заміни усіх фрагментів, що задовольняють умови, натиснути кнопку Заменить есе.Закриття документуДля закриття документувиконайте одну з наступних дій наступне: клацніть на кнопці Ш вікна документа; у меню Файл виберіть пункт Закрити. Створення нового документуДля створення нового документу виконайте одну з наступних дій: клацніть на кнопці J на стандартній панелі інструментів;- у меню Файл виберіть пункт Створити.Відкриття файлуЩоб відкрити файл, що зберігається на диску для виправлення, доповнення і збереження внесених змін, потрібно: клацнути на кнопці lJ панелі інструментів; в меню Файл вибрати пункт Відкрити для виклику діалогового вікнаВідкриття документа. У діалоговому вікні, що відкриється вибрати в графі Папка потрібний диск або папку, у якій знаходиться шуканий документ; знайти в списку файлів потрібний, виділити його; натиснути кнопку Відкрити (або клацнути на шуканому документі двічі).Є зручний спосіб швидко відкрити файл. Word зберігає імена останніх чотирьох файлів, з якими ви працювали, і виводить їх у нижній частині меню Файл. Щоб відкрити один з цих документів, просто зайдіть у меню Файл і клацніть на імені потрібного документа.160Додаток А, Основи роботи в табличному процесорі Excel Запуск ExcelДля запуску Excel необхідно скористатися меню, яку з'являється при натисненні на кнопку Пуск.Після запуску на екрані з'явиться головне вікно програми Excel (рис. 78).Q Micrnscrfi Fmtp| - Кнн/лі фдйл Правка ^ id J> ^JА І &*І ftн Г' _ В я м * * ^^^лиtтl/г^gт2^гvlcтg/>J EJ Hcrosrft Ечсті-ии Е В ^j« Рис. 78.Вікно табличного процесораТаблиця в Excel називається Робочим аркушем. Один файл Excel може містити декілька робочих аркушів і називається робочо/о книгою. Для вибору потрібного робочого аркуша в нижній частині вікна знаходяться ярлички робочих аркушів. Вибір аркуша здійснюється клацанням миші на потрібному ярличку.Відкриття робочої книгиДля відкриття робочої книги виконайте один і перерахованих способів: за допомогою кнопки t-Jf на панелі інструментів Стандартная, за допомогою команди Відкрити в меню Файл. Створення нової робочої книги.Існує два способи створення нової робочої книги:- в меню Файл вибрати команду Створити,клацнути на кнопці 1. панелі інструментів Стандартная. Введення данихВведення може здійснюватися тільки в активну (виділену) комірку. Зміна 161активної комірки здійснюється за допомогою кнопок управління курсором (стрілок) або маніпулятором типу миша.Введення інформації в активну комірку виконується в Рядк)> формул і закінчується натисненням кнопки Enter.Для видалення вмісту комірки необхідно встановити табличний курсор на потрібну комірку і натиснути кнопку Delete.ВидІлення блоку комірокДля виділення блоку комірок необхідно вказівник мишї встановити в лівому верхньому куту блоку, натиснути ліву кнопку миші і, не відпускаючи, перемістити вказівник в правий нижній куток блоку комірок. Відпустити ліву кнопку.АвтозаповненияАвтозаповненням можна створювати послідовності даних у вигляді арифметичної прогресії. Для цього в дві сусідні комірки вводять перший і другий члени арифметичної професії. Далі, виділивши блок вказаних комірок, протягуванням отримують всі потрібні значення арифметичної прогресії (за правий нижній куток виділеного блоку протягують до комірки, що містить останній член прогресії).АвтосумуванияВстановити табличний курсор в комірку, в якій повинна знаходитися сума. Вказівником миші натиснути кнопку Автосумма на панелі інструментів.Якщо блок, що вказаний пунктиром, відповідає потрібному діапазону сумування, натиснути кнопку Enter. В протилежному випадку за допомогою вказівника миші виділити потрібний блок і натиснути кнопку Enter.Введения математичних формулВведення формули повинне починатися зі знаку = (дорівнює). Всі записи в формулах повинні здійснюватися латинськими буквами (для зміни мови натиснути комбінацію кнопок Alt+Shift або Ctrl-i-ShLft). В формулах використовуються знаки: + (додавання), - (віднімання), * (множення), / (ділення), Л (піднесення до степеня), а також спеціальні функції (кнопка Вставка функции (f4) на панелі інструментів Стандартная). Для задания послідовності операцій використовуються круглі дужки ().Копіювання формулКопіювання формул здійснюється аналогічно звичайній процедурі копіювання. При цьому відбувається автоматична зміна адрес комірок, тобто результат в наступній комірці обраховується для даних, отриманих із нових комірок (зазвичай сусідніх з початковими). Якщо необхідно, щоб адреса якоїсь комірки в формулі залишалась незмінною, то перед буквою і цифрою адреси комірки ставиться знак S. Наприклад, $G$23.Друк результатів162Друк всього робочого листа:перед друком необхідно переконатися, що вміст і форма документа, що виводиться мають потрібний вигляд. Для цього на панелі інструментів за допомогою миші натиснути кнопку Предварительный просмотр;у випадку якщо документ задовольняє всі вимоги, на панелі інструментів натиснути кнопку Печать.,в діалоговому вікні друку, що з'явилося натиснути кнопку ОК.Друк фрагменту робочого листа:- виділити блок потрібного фрагменту за допомогою миші;відкрити розділ меню Файл, вибрати пункт Область печати і підпункт Задать;- далі перейти до пункту 1.1 друку всього робочого листаДрук однієї діаграми: активувати потрібну діаграму; далі перейти до пункту 1.1 друку всього робочого листа Форматування рамки таблицівиділити блок комірок, вздовж границь яких повинна бути проведена лінія;за допомогою миші на панелі інструментів Фор.матыроеание натиснути стрілку справа від кнопки Граница.в меню, що відкрилося вибрати місцезнаходження і тип рамки. Клацнути лівою кнопкою миші.якщо рамка сформована не повністю, повторити процедуру, починаючи з п.1.Для видалення рамки слід виділити відповідний блок комірок, повторити п.2 і в меню, що відкриється вибрати варіант без решки (лівий верхній квадрат).Відміна дійДля відміни дій використовуються кнопки ' і на панелі інструментів Стандартная.Повідомлення про помилки#ДЕЛ/О! - спроба ділення на нуль. #ИМЯ? - ім'я функції задано невірно. #Н/Д- немає даних в комірці.#ЧИСЛО! - проблема з числовим значенням (наприклад, комірка містить від'ємне число замість додатного).1631   ...   57   58   59   60   61   62   63   64   65


Роки У = 1,7493Ln(x;i + 17,005

R'= 0,9716

Р ис. 55. Експериментальні дані, апроксимовані логарифмічною кривою

Проаналізувавши рисунок 55, стверджуємо, що рівняння логарифмічної апроксимуючої кривої поступається в точності апроксимації поліноміальної кривої R2 = 0,9716 < 0,986. Тому, за відсутності будь - яких теоретичних міркувань, можна вважати, що найкращою апроксимацією є апроксимація поліноміальною функцією другого степеня (з двох розглянутих варіантів).

Демонстраційний приклад 2

Після викиду я довитої речовини його концентрація (мг/л) у водоймищі змінювалась у відповідності з наступною таблицею:

Час після викиду (і од.)
]
3
5
8

Концентрація речонини

(mi/jj)
8,0



J,o
0,3

Визначимо тип функціональної залежності зміни концентрації речовини з часом і оцінимо її концентрацію в момент викиду. Для цього введемо дані в електронну таблицю та побудуємо діаграму. Оскільки необхідно будувати динаміку зміни концентрації речовини відповідно з вказаними проміжками часу (нерівномірними) - будуємо діаграму Точечная (рис. 56).

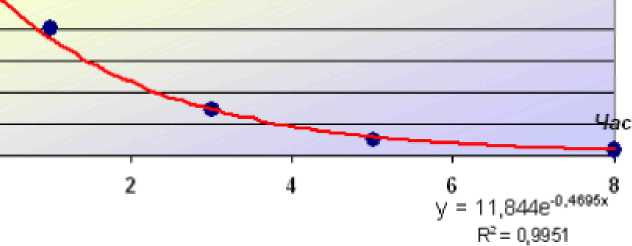
Апроксимуємо отриману криву. Оскільки крива візуально походить на експоненту і з теоретичних міркувань ймовірніше, що закон зміни -експоненціальний, доцільно апроксимувати криву зміни концентрації експоненціальною функцією. Дія цього викликаємо контекстне меню графіка, в якому вибираємо пункт Добавить линию тренда. В діалоговому вікні, що з'явилося, Лінія тренда на вкладці Тип вибираємо тип лінії тренда Експоненціальна. Потім відкриваємо вкладку Параметры і встановлюємо прапорці в поля показывать уравнения на диаграмме та поместить на диаграмму величину достоверности аппроксимации (RA2). Крім цього, для того щоб оцінити концентрацію речовини у водоймищі в момент викиду, в полі Прогноз назад на встановлюємо / периодов. Після чого натискаємо кнопку ОК. В результаті отримуємо апроксимуючу криву (рис. 57).

109

Як видно з рисунка 57, рівняння експонентної апроксимуючої функції для залежності концентрації від часу має вигляд у = 11,844е° 95. При цьому точність апроксимації досить висока R2 = 0,9951', що дозволяє вважати опис процесу зміни концентрації речовини у водоймищі експоненціальною функцією адекватним. Розрахункова оцінка концентрації речовини в момент викиду, як видно з графіка, становить близько 12 мг/л. Точнішу цифру отримуємо з рівняння у =
1   ...   37   38   39   40   41   42   43   44   ...   65

І1,844ег при х = 0 (уі>= 11.84 мг/л).


□ Microsoft Excel -
Кннгаі












] Файл Оээв*а
Вид Встій
» Форцат Сервис
Данные фчнс
Справка



. J ^/ Я J J



"ДІЛ -ii-



1 A * •
Al f

я+ ;

03 і
A
3
С
D
E
и.

1
Час після викиду (год.)
1



5
8



7
Концентрація речовини ції їй
8
2,8
1
0,3



q









♦ Кон
центрвція









id -















1 6

2 -п .















в

9 10 11 12

ІЗ 14















*







♦
*

15 16 17
Є і- ЛІ






час



Рис. 56. Введення ()аних в електронну таблицю ти побудова точкової діаграми

• Концентрація

Экспоненциагъный (Концентрація)





14

р 1г

I 10 1 8

I:

2

и

Р ис. 57. Експериментальні бані, апрокси.\іовані експонентною кривою

Практичні завдання

по

Завдання 1. Візуалізація меди ко-статистичних даних (за допомогою діаграми).

Побудуйте діаграму залежності кількості захворілих від часу на основі статистичних даних розвитку епідемії (табл. 25).



[я 25. Статистичні дані розвитку
вяшеміі









День розвитку епідеми
І
2
3
4
5
6
7
8
9
10

Кількість захворілих протягом дня на 10 тис. населення
U
4,1
9,2
15,3
24,8
35,1
48,6
63,4
81,3
102,5

Вказівки до виконання завдання

1). Заповніть даними робочий лист електронної таблиці.

2). Для побудови діаграми скористайтеся схемою 2. Відредагуйте діаграму таким чином, щоб крок по часу відповідав 5 діб. Для цього скористайтеся схемою 3.

23, Завдання 2. Побудова прогнозу розвитку епідемії

Виконайте функціональну апроксимацію статистичних даних розвитку епідемії за даними таблиці 25.

Вказівки до виконання завдання

1) Апроксимуйте отриману криву за допомогою степової функції. Рівняння та величину достовірності апроксимації покажіть на діаграмі. Для побудови функції прогнозу та встановлення відповідних параметрів скористайтеся схемою 4.

2} Визначити на основі отриманої аналітичної залежності кількість захворілих на 10 тис. населення на 11, 13, 15 день від початку розвитку епідемії.

3) Визначити, у який день кількість захворілих на 10 тис. населення перевищить поріг

Смотрите также файлы