ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 47
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и ВЫСШЕГО образования Российской федерации
МОСКОВСКИЙ КОЛЛЕДЖ ГЕОДЕЗИИ И КАРТОГРАФИИ
федерального государственного бюджетного образовательного учреждения высшего образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОДЕЗИИ И КАРТОГРАФИИ»
(МКГиК)
КОНТРОЛЬНАЯ РАБОТА № 1
по междисциплинарному курсу
МДК 01.01 ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ КООРДИНАТ И ВЫСОТ ПУНКТОВ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ И СЕТЕЙ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ.
ПМ.01 ВЫПОЛНЕНИЕ РАБОТ ПО СОЗДАНИЮ ГЕОДЕЗИЧЕСКИХ, НИВЕЛИРНЫХ СЕТЕЙ И СЕТЕЙ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ
Вариант № 1
Выполнил студент заочного отделения группы ПГС-4
Казаков Роман Викторович
Проверил преподаватель
_______________/Маслов Е.В.
Оценка______________________
Дата проверки__________________
Зарегистрировал зав. заочным отд.
_______________/Трущелёва Н.В.
МОСКВА 2022
Содержание
Задание №3. Вычисление теоретической суммы превышений. 3
Задание №4. Оценка разности нормальных высот на уровенной поверхности. 4
Задание №5. Вычисление аномалий силы тяжести. 6
Список литературы 8
Задание №1. Вычисление геопотенциального числа
Геопотенциальное число определяется формулой:
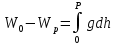
Обычно определяют не геопотенциальное число, а разность геопотенциальных чисел между реперами, например, реперами 1-2, т.е. разность потенциалов
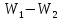 . Ее можно найти с помощью выражения:
. Ее можно найти с помощью выражения: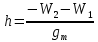
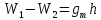
В качестве
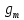 используем среднее значение силы тяжести из ее значений на реперах.
используем среднее значение силы тяжести из ее значений на реперах.Уравненные разности потенциалов – разности потенциалов, исправленные равномерным распределением суммы (∑стлб.5/Nреперов):
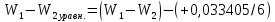
| Репер | Превышение  , м. , м. | Сила тяжести  , мГал , мГал | 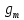 , мГал , мГал | Разность потенциалов, кГал∙м | Геопотенциальное число, кГал∙м | ||
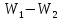 | 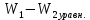 | 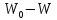 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 21 | | 980 992,0 | | | | 13,754259 | |
| | +184,2120 | | 980 945,9 | +180,702006 | +180,696439 | | |
| 27 | | 980 899,8 | | | | 194,450698 | |
| | -113,4040 | | 980 875,8 | -111,235239 | -111,240807 | | |
| 52 | | 980 851,8 | | | | 83,209891 | |
| | -51,0840 | | 980 858,2 | -50,106158 | -50,111725 | | |
| 60 | | 980 864,5 | | | | 33,098166 | |
| | -24,5991 | | 980 863,8 | -24,128367 | -24,133934 | | |
| 59 | | 980 863,1 | | | | 8,964232 | |
| | +11,9918 | | 980 903,3 | +11,762796 | +11,757229 | | |
| 34 | | 980 943,5 | | | | 20,721460 | |
| | -7,0967 | | 980 967,8 | -6,961634 | -6,967201 | | |
| 21 | | 980 992,0 | | | | 13,754259 | |
| ∑ | +0,020 | | | +0,033405 | 0 | | |
Задание №2. Вычисление нормальных и динамических высот
Нормальную высоту в первом приближении можно принять равной:
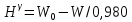
Во втором приближении:
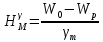 , где
, где 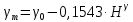
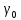 - нормальная сила тяжести на эллипсоиде на широте В. Находим, используя формулу Гельмерта:
- нормальная сила тяжести на эллипсоиде на широте В. Находим, используя формулу Гельмерта: 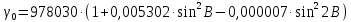
Расчеты sin(значение угла B представлено десятичной дробью):
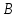 | 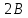 | 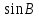 | 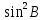 | 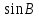 | 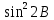 |
| 49,05 | 98,10 | 0,755282 | 0,570451 | 0,990024 | 0,980147 |
| 48,73 | 97,47 | 0,751648 | 0,564975 | 0,991521 | 0,983113 |
| 47,90 | 95,80 | 0,741976 | 0,550528 | 0,994881 | 0,989788 |
| 47,67 | 95,33 | 0,739239 | 0,546475 | 0,995671 | 0,991360 |
| 47,67 | 95,33 | 0,739239 | 0,546475 | 0,995671 | 0,991360 |
| 48,50 | 97,00 | 0,748956 | 0,560935 | 0,992546 | 0,985148 |
Для вычисления динамической высоты используем любую из двух формул:
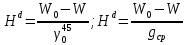 В данной работе использую первую формулу.
В данной работе использую первую формулу.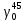 - значение нормальной силы тяжести на широте 45̊.
- значение нормальной силы тяжести на широте 45̊. 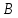 | 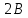 | 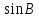 | 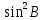 | 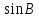 | 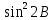 |
| 45,00 | 90,00 | 0,707107 | 0,500000 | 1,000000 | 1,000000 |
Используя формулу Гельмерта, получим:
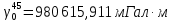
| Репер | Широта 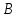 | Уравненное геопотенциальное число | Нормальная сила тяжести | Нормальная высота | Динамическая высота | Разность высот | |||
| I приближение | II приближение | ||||||||
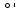 | 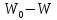 , кГал∙м , кГал∙м | 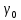 , , мГал∙м | 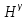 , м , м | 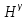 , м , м | 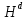 , м , м | 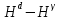 , мм , мм | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 21 | 49 03 | 13,754259 | 980 981,370 | 14,0350 | 14,0209 | 14,0261 | 5,194 | ||
| 27 | 48 44 | 194,450698 | 980 952,954 | 198,4191 | 198,2325 | 198,2945 | 61,944 | ||
| 52 | 47 54 | 83,209891 | 980 877,996 | 84,9081 | 84,8332 | 84,8547 | 21,540 | ||
| 60 | 47 40 | 33,098166 | 980 856,967 | 33,7736 | 33,7443 | 33,7524 | 8,116 | ||
| 59 | 47 40 | 8,964232 | 980 856,967 | 9,1472 | 9,1392 | 9,1414 | 2,233 | ||
| 34 | 48 30 | 20,721460 | 980 931,991 | 21,1443 | 21,1243 | 21,1311 | 6,739 | ||
