ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 46
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание №3. Вычисление теоретической суммы превышений.
в качестве
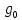 можно принять наименьшее значение из стлб.3. - 980 858,2
можно принять наименьшее значение из стлб.3. - 980 858,2| Репер | 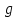 , мГал , мГал | 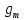 , мГал , мГал | 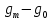 , мГал , мГал | 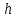 , м. , м. | 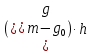 , кГал∙мм , кГал∙мм | Длина секции 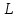 , км , км |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 21 | 980 992,0 | | | | | |
| | | 980 945,9 | 87,750 | +184,2120 | +16,1646 | 68,97 |
| 27 | 980 899,8 | | | | | |
| | | 980 875,8 | 17,650 | -113,4040 | -2,0016 | 117,10 |
| 52 | 980 851,8 | | | | | |
| | | 980 858,2 | 0 | -51,0840 | 0 | 39,00 |
| 60 | 980 864,5 | | | | | |
| | | 980 863,8 | 5,650 | -24,5991 | -0,1390 | 92,08 |
| 59 | 980 863,1 | | | | | |
| | | 980 903,3 | 45,150 | +11,9918 | +0,5414 | 112,11 |
| 34 | 980 943,5 | | | | | |
| | | 980 967,8 | 109,600 | -7,0967 | -0,7778 | 119,90 |
| 21 | 980 992,0 | | | | | |
| ∑ | | | | +0,02 | +13,7877 | 549,16 |
Теоретическая сумма превышений вычисляется по формуле:
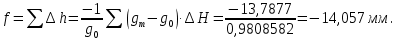
Ожидаемая ошибка нивелирования I класса:
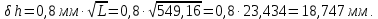
Задание №4. Оценка разности нормальных высот на уровенной поверхности.
Основной формулой для оценки разности нормальных высот на уровенной поверхности является формула:
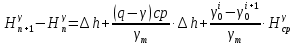
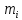 – измеренное превышение;
– измеренное превышение; 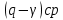 – средняя по секции аномалия в свободном воздухе;
– средняя по секции аномалия в свободном воздухе;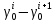 – разность значений нормальной силы тяжести на эллипсоиде на широте реперов;
– разность значений нормальной силы тяжести на эллипсоиде на широте реперов;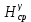 – средняя высота секции нивелирования;
– средняя высота секции нивелирования;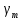 – значение нормальной силы тяжести, вычисленное для средней широты и высоты секции.
– значение нормальной силы тяжести, вычисленное для средней широты и высоты секции.Второй и третий члены формулы иногда называют поправками в измеренное превышение за непараллельность уровенных поверхностей реального (второй член) и нормального (третий член) гравитационного поля.
В данном задании оценка производится для двух пунктов, расположенных на одной уровенной поверхности (крайние северная и южная точки водного объекта), поэтому рабочая формула имеет вид:
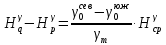
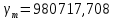
Значения нормальной силы тяжести на поверхности отсчетного эллипсоида считаем по формуле Гельмерта:
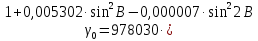 )
)Расчеты sin(значение угла B представлено десятичной дробью):
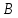 | 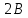 | 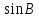 | 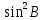 | 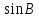 | 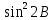 |
| 46,43 | 92,87 | 0,724573 | 0,525006 | 0,998749 | 0,997499 |
| 45,82 | 91,63 | 0,717113 | 0,514252 | 0,999594 | 0,999188 |
Протяженность объекта с юга на север по меридиану можно определить по формуле:
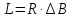 , где
, гдеR-средний радиус Земли (6371 км.);
B-разность широт в радианах.
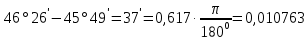
Общая формула расчета ошибки нивелирования:
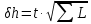 , где
, гдеt - случайная ошибка нивелирования на 1 км. хода;
∑L - длина полигона в километрах.
Ожидаемая ошибка нивелирования I класса:
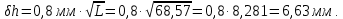
Ожидаемая ошибка нивелирования II класса:
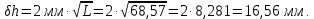
Объект: Алаколь
| Широта | 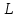 , км , км | 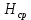 , м , м | 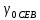 , мГал∙м , мГал∙м 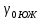 , мГал∙м , мГал∙м | 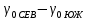 , мГал∙м , мГал∙м | 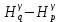 , мм , мм | 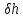 , мм , мм |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 46° 26' | 68,57 | 50 | 980 745,5972 | 55,78 | 2,84 | 6,63 - I кл. |
| 45° 49' | 980 689,8187 | 16,56 - II кл. |
Задание №5. Вычисление аномалий силы тяжести.
В данном задании необходимо вычислить аномалии силы тяжести в свободном воздухе и аномалии Буге для десяти гравиметрических пунктов.
 – широта и долгота гравиметрического пункта;
– широта и долгота гравиметрического пункта; 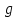 – измеренное значение силы тяжести.
– измеренное значение силы тяжести.Нормальное значение силы тяжести на поверхности эллипсоида, находим по формуле Гельмерта:
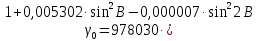 )
)Расчеты sin(значение угла B представлено десятичной дробью):
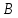 | 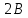 | 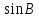 | 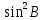 | 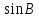 | 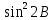 |
| 35,005 | 70,009 | 0,573641 | 0,329064 | 0,939746 | 0,883123 |
| 35,007 | 70,014 | 0,573674 | 0,329102 | 0,939774 | 0,883176 |
| 35,017 | 70,034 | 0,573822 | 0,329272 | 0,939897 | 0,883407 |
| 35,017 | 70,034 | 0,573822 | 0,329272 | 0,939897 | 0,883407 |
| 35,025 | 70,050 | 0,573931 | 0,329397 | 0,939989 | 0,883579 |
| 35,039 | 70,078 | 0,574134 | 0,329630 | 0,940157 | 0,883896 |
| 35,062 | 70,124 | 0,574463 | 0,330007 | 0,940431 | 0,884410 |
| 35,067 | 70,134 | 0,574532 | 0,330087 | 0,940488 | 0,884518 |
| 35,075 | 70,150 | 0,574648 | 0,330221 | 0,940585 | 0,884700 |
| 35,078 | 70,155 | 0,574686 | 0,330264 | 0,940616 | 0,884759 |
