Файл: Пояснительная записка к курсовому проекту по дисциплине Основы теории надежности оценка работоспособности систем тягового электроснабжения с учетом надежности ее основных элементов.docx

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»

(ФГБОУ ВПО ПГУПС)
Кафедра «Электроснабжение железных дорог»

Пояснительная записка к курсовому проекту

по дисциплине «Основы теории надежности»

«ОЦЕНКА РАБОТОСПОСОБНОСТИ СИСТЕМ ТЯГОВОГО ЭЛЕКТРОСНАБЖЕНИЯ С УЧЕТОМ НАДЕЖНОСТИ ЕЕ ОСНОВНЫХ ЭЛЕМЕНТОВ»

Выполнил студент Группа ЭС-104		В.А. Павлов
Руководитель доцент		В.М. Варенцов
Нормоконтролёр доцент		В.М. Варенцов

Санкт-Петербург

ПГУПС

2015

Содержание

Введение

---

Целью курсового проекта является выработка навыков применения теории надежности при оценке работоспособности систем тягового электроснабжения с учетом надежности ее основных элементов.

В процессе проектирования необходимо выполнить следующие расчеты:

1. 
   Расчет параметров надежности элементов системы электроснабжения.
   

По данным об ежегодных отказах элементов определить показатели надежности работы, интенсивность отказов, функцию плотности распределения вероятности отказа в зависимости от времени и наработку на отказ.

2. 
   Подобрать непрерывную функцию закона распределения.
   

Подобрать параметры для экспоненциального и нормального законов распределения. Построить зависимости показателей надежности от времени.

3. 
   Рассчитать доверительный интервал при заданных доверительных вероятностях
   
4. 
   По заданной зависимости изменения параметра от времени, либо от числа проходов токоприемника, либо от изменения грузопотока и заданного ограничения параметра определить средний срок службы элемента и его интенсивность отказов.
   
1. 
   Расчет надежности систем
   
   1. 
      Расчет надежности блока защиты
      
   2. 
      Расчет надежности выпрямителя
      
   3. 
      Расчет надежности системы электроснабжения без восстановления
      
   4. 
      Расчет надежности системы электроснабжения с восстановлением
      
   5. 
      Расчет надежности системы с учетом износа оборудования
      

1. Расчет параметров надежности элементов системы электроснабжения

Таблица 1 – исходные данные

№ варианта	N0	Число отказавших элементов n
Годы
10	130	18	16	13	11	10	11	9	8	10	14

---

Вероятность безотказной работы Р(t) – вероятность того, что рассматриваемый элемент или система в заданный промежуток времени останется в рабочем состоянии.

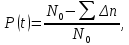(1)

где N­₀ – неремонтируемые элементы, находящиеся в работе 10 лет; Δn – число отказавших элементов в каждый год работы.





















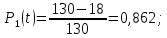
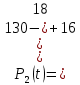
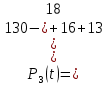
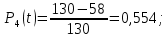
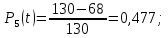
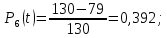
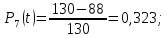
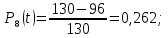
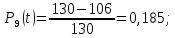
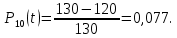
Вероятность отказа Q(t) – вероятность того, что рассматриваемый элемент или система в заданный промежуток времени выйдет из строя.

( )

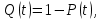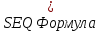
Пример расчета:







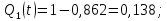
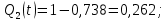
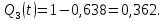
Функция плотности распределения вероятности безотказной работы f(t) – приращение отказавших элементов за время t.

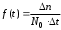, (2)

где Δt = 1 год.

Пример расчета:

---

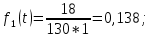
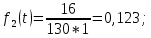
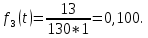
Интенсивность отказов (t) – отношение числа отказавших элементов или систем в единицу времени к числу элементов, исправно работающих в данный отрезок времени.

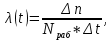(3)

где N_раб – число элементов, оставшихся в работе в рассматриваемый интервал времени от начала испытаний, (напр. для первого года,
N_ср =N₀-n₁, для второго года, N_ср =N₀-n₁–n₂).


Пример расчета:













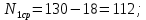
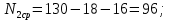
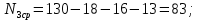
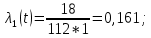
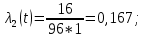
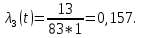
Средне время безотказной работы (наработка на отказ) Т_ср – есть математическое ожидание времени работы элемента или системы до его отказа.

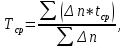(4)

где t_ср – среднее время от начала отсчета до интервала времени, в котором отказали nэлементов.


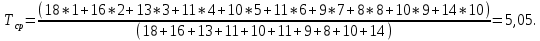
Таблица 2 – результаты расчетов

Годы	Δn	Р(t)	Q(t)	Nср	f(t)	λ(t)	Tср
1	18	0,862	0,138	112	0,138	0,161	5,05
2	16	0,738	0,262	96	0,123	0,167
3	13	0,638	0,362	83	0,100	0,157
4	11	0,554	0,446	72	0,085	0,153
5	10	0,477	0,523	62	0,077	0,161
6	11	0,392	0,608	51	0,085	0,216
7	9	0,323	0,677	42	0,069	0,214
8	8	0,262	0,738	34	0,062	0,235
9	10	0,185	0,815	24	0,077	0,418
10	14	0,077	0,923	10	0,108	1,400

---

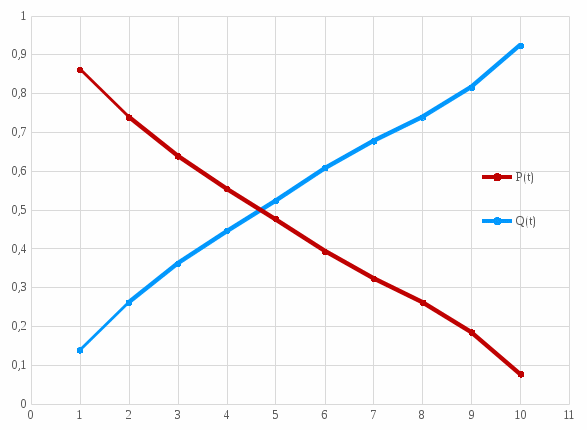
Рисунок 1 – зависимость вероятности безотказной работы элементов P(t) и вероятности отказа Q(t) от времени



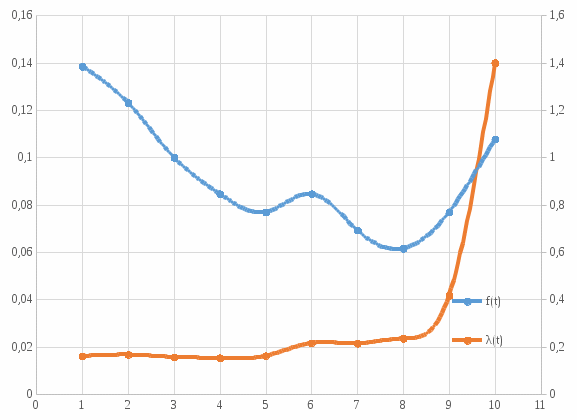
Рисунок 2 – зависимость вероятности безотказной работы элемента f(t) и интенсивности отказа λ(t) от времени

2.   1   2   3   4   5   6

---