Файл: Otvety_po_fizike_2013_1.doc

7Й вопрос. Момент инерции. Теорема Штейнера. Момент инерции однородных тел простейшей формы(стержень,цилиндр,шар).Расчет момента инерции однородного диска.

Момент инерции системы тела относительно данной оси называется физическая величина, равная сумме произведений масс N материальных точек системы на квадраты их расстояний до рассматриваемой оси.

J=(знак сум.:i=1;n)(mi•ri^2)

Теорема Штейнера-момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно парралельной оси, проходящей через центр масс C тела ,сложенному с произведением массы m тела на квадрат расстояния а между осями:

J=Jc+ma^2

Полый тонкостенный цилиндр радиусом R(ось симметрии) J=mR^2

Сплошной цилиндр или диск радиусом R(ось симметрии) J=mR^2/2

Прямой тонкий стержень длиной l(ось перпенд-на стержню и проходит через его середину) J=ml^2/12

Прямой тонкий стержень длиной l(ось перпенд-на стержню и проходит через его конец) J=ml^2/3

Шар радиусом R(ось проходит через центр) J=2mR^2/5

(см рис2).p(ро)-плотность матер.;r,dr.

dV=2Пи•r•dвки

dm=pdv

J=(простой интег)(dm•r^2)=(интег от 0 до R)(p•2Пи•r•dr•b•r^2)=2Пи•b•p(интегр от 0 до R)(r^3dr)=2Пи•b•p•R^4/4=(m=ПиR^2bp)=mR^2/2

8Й вопрос. Основной закон динамики вращ. Дв. ,его выводы на примере одной частицы. Внешние и внутренние силы.

Основной закон динамики вращательного движения твердого тела формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.

Производная момента импульса по времени, относительно полюса О равна моменту внешних сил относительно полюса.

dL/dt=M

(ситема из 3х ур-ий):

dLx/dt=Mx

dLy/dt=My

dLz/dt=Mz

Пусть вращение тела происходит вокруг оси z, т.е. вектор w сонаправлен с осью z,тогда

Lz=Jz•w

dLz/dt=d(Jz•w)/dt=Jz•dw/dt=Jz•E=Mz,где Е--эпсилон.

Mz=Jz•E

Вывод:

Везде вектора!!! L=[rp]=[r,mv]

dL/dt=d([r,mv])/dt=[dr/dt,mv]+[r,mdv/dt]=m[v,v]+[r,ma]=(т.к. m[v,v]=0 и ma=F)=[r,F]

9 й вопрос. Закон сохранения момента импульса для замкнутой системы. Сохраняющиеся величины-интегралы движения: законы сохранения энергии, импульса ,момента импульса .Кинетическая энергия частицы ,ее связь с работой результирующей силы.

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.         Это один из фундаментальных законов природы.         Аналогично для замкнутой системы тел, вращающихся вокруг оси z:

         отсюда                  или         .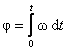

Импульс замкнутой системы сохраняется.

В системе тел между которыми действуют только консервативные силы- полная энергия сохраняется.

Кинетическая энергия механической системы -энергия механического движения этой системы.

Зависит от выбора системы отсчета.

Момент импульса замкнутой системы сохраняется, и не изменяется с течением времени.

В замкнутой системе момент внешних сил M=0 и dl/dt=0 откуда L=const

Гироскоп-массивное однородное тело, вращающиеся с большой угловой скоростью около оси своей симметрии, являющейся свободной осью.

Гироскоп сохраняет свое положение в пространстве тк моменты сил тяжести и трения относительно центра масс равны 0. Следовательно момент импульса гироскопа сохраняет свою величину и направления.

Чтобы ось гидроскопа изменила свое направление в пространстве,необходимо отличие от нуля момента внешних сил.Если момент внешних сил, приложенных к вращающемуся гидроскопу, относительно его центра масс отличен от нуля, то наблюдается явление,которое назыв. гидроскопическим эффектом.Оно состоит в том, что под действием пары сил F,приложенных к оси вращающегося гидроскопа,ось гидроскопа поворачивается вокруг прямой О3О3,а не вокруг прямой О2О2.

10Й вопрос. Потенциальная энергия взаимодействия. Полная мех. Энергия системы взаимодействующих друг с другом частиц ,находящихся во внешнем поле сил.

Потенциальная энергия-мех. энергия системы тел,определяемая их взаимным расположением и характером сил взаимодействия м-ду ними.

Если тела взаимодействуют силовыми полями (гравитация и тп) то они называются потенциальными а силы консервативными.

Зависит только от конфигурации системы и ее положения по отношению к внешним телам.

Полная мех. энергия ситемы- энергия мех. движения и взаимодеиствия:

Е=Т+П, т.е. равна сумме кинетической и потенциальной энергии.

11Й вопрос. Потенциальная энергия во внешнем поле сил. Однородное и стационарное поле. Консервативные силы. Полная мех. Энергия. Работа консервативных и неконсервативных сил.

Стационарное поле отличается от электростатического не только тем, что заряд источника этого поля непрерывно восстанавливается, но и тем, что такое поле обнаруживается как вокруг проводящих тел, так и внутри этих тел.

Работа кинитической энергии совершается движение вызванными силой действующей на тело

Работа консервативной силы равна приращению потенциальной энергии.

12Й вопрос. Закон всемирного тяготения. Гравитационное поле ,его напряженность.

Закон всемирного тяготения Сила взаимодействия м-ду частицами м1 и м2 пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния м-ду ними.

F12=Km1m2/r^2, где К=6,6722•10^(-4) Н•м^2./кг^2 - гравитационная постоянная.

Расчет показывает,что при взаимод. тел, обладающих сферической симметрии(сплошной или полый шар), сила взаим. равна взаим. точечных масс равных массами этих тел и расположенных в центре этих тел..

Гравитационное взаимодействие м-ду телами осущ-ся с помощью поля тяготения или гравитационного поля.Это поле порождается телами и явл. формой существования материи.Основное св-во поле тяготения заключается в том, что на всякое тело массой m,внесенное в это поле, действует сила тяготения, т.е. F=mg

Вектор g не зависит от m и назыв. напряженностью поля тяготения.Напряженностью поля тяготения определяется силой, действующей со стороны поля на матер. точку единичной массы, и совпадает по направлению с действующей силой.Напряженность есть силовая хар-ка поля тяготения.

13Й вопрос. Первая,вторая и третья космические скорости.

I.Для того чтобы тело устойчиво двигалось по круговой орбите вокруг земли с радиусом движения мало отличающего от радиуса земли, необходимо чтобы силы согласно второму закону Ньютона

GmM/R=mV1^2/R

V1=Кореннь из GM/R=(т.к mg=GmM/R^2)=sqrt gR

V1=8*10^3 м/с=8 км/с

II. Для того, чтобы тело покинуло пределы земного притяжения и попало в область притяжения Солнца

E=E(бесконеч)

E=mV2^2/2-GmM/r

Е(бесконеч)=mV(беск)^2/2

V2=Vmin при V(бескон)=0 =>

mV2^2/2=GmM/R =>

V2=корень 2GM/R=V1 на Корень из 2=11,2 км/с

III. Для того, чтобы выйти за пределы солнечной системы тело должно обладать скоростью V3=73 км/с при запуске против направления орбитального движения Земли.

V3=17 км/с - по направлению движения.

Если не учитывать орбитальную скорость Земли относительно Солнца и притяжение относительно Земли то V3=42 км/с

V3max=72 км/с

V3min=12 км/с

14Й вопрос. Неинерциальные системы отсчета. Силы инерции. Центробежная сила инерции .Сила Кориолиса.

Неинерциальные системы отсчёта - те, которые движутся относительно инерциальной системы с ускорением.

Силы инерции действуют на нитку с шариком прикреплённым к потолкувагона двигающегося с ускорением a.

в инерц. СО ma=F=T+mg

в инерц СО ma=F+Fин Fин=-(T+mg)=-ma

Для того, чтобы заставить шарик катиться по вращяющемуся диску вдоль радиуса, используем жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения, равномерно и прямолинейно, со скоростью V'.. При отклонении шарика стержень действует на него с некоторой силой F. Относительно диска (вращающейся СО) шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила F уравновешивается приложенной к шарику силой инерции F(k), перпендикулярной к скорости V'. Эта сила называется Кориолисовой силой инерции. F(k)=2m[V' • w] ,w - угловая скорость.

Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчёта (Земли). Этим объясняется то, что если тело движется в северном полушарии на север, то сила Кориолиса будет направленна на восток, если тело движется на юг то отклонится на запад.

Центробежная сила инерция действует на шарик, закреплённый к оси вращающегося диска

15Й вопрос. Релятивистская механика. Постулаты Эйнштейна. Длительность событий в разных системах отсчета. Размеры тела в направлении движения и в направлении, поперечном движению.

I. Постулат Эйнштейна

Принцип относительности - никакие опыты (механические, электрические, оптические), проведенные внутри данной инерц. СО, не дают возможности обнаружить, покоится она или движется равномерно и прямолинейно, и все законы природы инвариантны по отношению к переходу от одной инерциальной СО к другой.

II. Принцип инвариантности скорости света, скорость света в вакуме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных СО.

Длительность события в разных СО происходит в некоторой точке, наименьшая в той инерциальной системе отсчёта, относительно которой эта точка неподвижна.

Часы, движущиеся относительно инерциональной СО, идут медленнее покоящихся часов

t'=t • sqrt1-b^2

Из этого отношения вытекает, что t<t' , т.е. длительность события, происходящего в некоторой точте, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.