Файл: Пояснительная записка к курсовому проекту по дисциплине Информатика Выполнил студент гр.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждениевысшего образования
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждениевысшего образованияТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕТРОНИКИ
(ТУСУР)
Кафедра сверхвысокочастотной и квантовой радиоэлектроники (СВЧ и КР)
Численные методы интегрирования Пояснительная записка к курсовому проекту по дисциплине
«Информатика»
Выполнил студент гр
«»2020 г.
Руководитель
доцент кафедры СВЧ и КР к. ф.-м. н.
А.О. Семкин
«»2020 г.
Томск 2020

Реферат
Метод левых прямоугольников, метод правых прямоугольников, метод трапеций, метод Симпсона.
Объектом исследования является численное интегрирование с применением языка C++ .
Цель работы состоит в разработке программы на языке C++ демонстрирующей интегрирование различными методами и получении результатов.
К полученным результатам относятся численные значения интеграла, вычисленного разными способами.
1.1. В результате выполнения курсового проекта было разработано приложение, вычисляющее определенный интеграл: ;
 Министерство науки и высшего образования Российской Федерации
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
(ТУСУР)
Кафедра сверхвысокочастотной и квантовой радиотехники (СВЧиКР)
"УТВЕРЖДАЮ"
Зав. каф. СВЧиКР
Шарангович С.Н. ""2018г.
ЗАДАНИЕ
На курсовую работу по дисциплине «Информатика» студенту группы з-17 Заочного и вечернего факультета Алейникову Александру Викторовичу
-
Тема работы: Численные методы интегрирования (утверждено приказом по университету от2018г. №) -
Срок сдачи работы на кафедру:2018г. -
Цель работы: разработка приложения на языке C++, выполняющего интегрирование заданной функции в заданных интервалах. -
Исходные данные:-
Функция задана в следующем виде: -
 Необходимо разработать приложение, вычисляющее определенный интеграл:
Необходимо разработать приложение, вычисляющее определенный интеграл: -
Приложение должно быть разработано на языке программирования C++.
-
-
Вопросы, подлежащие разработке:-
Провести аналитический обзор литературы по численным методам интегрирования. -
Разработать алгоритм решения задачи, начертить блок-схему. -
Реализовать разработанный алгоритм на языке C++. Приложение должно выводить на экран результат вычисления интеграла от заданной функции. -
Провести отладку приложения на ПК. -
Проверить работоспособность разработанного приложения путем сравнения результатов вычисления интеграла с аналогичными вычислениями в любом математическом пакете (предпочтительно: MathCAD , Matlab).
-
-
Содержание пояснительной записки:-
Титульныйлист. -
Реферат. -
Лист задания с подписью преподавателя. -
Содержание. -
Введение. Постановка задачи. -
Аналитический обзор литературы. -
Разработка алгоритма решения задачи (блок-схема алгоритма обязательна). -
Описание исходного кода программы (описание работы функций, назначения переменных ит.д.). -
Результаты отладки приложения на ПК (скриншоты окна работающего приложения). -
Результаты проверки работоспособности приложения, сравнение результатов вычислений с математическими пакетами (описание кода математического пакета, скриншоты результатов вычислений). -
Выводы по проделанной работе. -
 Список использованной литературы.
Список использованной литературы. -
Приложения с исходным кодом программы.
-
-
Рекомендуемая литература:-
Язык программирования C++. Лекции и упражнения / С. Прата. – М.: ДиаСофт. – 2002. –896с. -
Qt. Профессиональное программирование на C++ : Наиболее полное руководство / М. Шлее. – СПб.: БХВ-Петербург, 2005. – 544с. -
Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль / А.Е. Мудров–Томск: МП "РАСКО", 1991. – 272с. -
Дополнительную литературу студент ищет самостоятельно.
-
Дата выдачи задания""2018г.
Подпись руководителя// Подпись студента//
 Содержание
СодержаниеЧисленное интегрирование 8
-
Заключение 15
Список используемых источников 20
-
 Введение
Введение
Необходимо рассчитать значение данного интеграла следующими методами:
-
методом левых прямоугольников; -
методом правых прямоугольников; -
методом трапеций; -
методом Симпсона; -
методом «трехвосьмых».
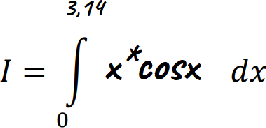
-
 Постановка задачи Разрабатываемая программа должна обладать следующими
Постановка задачи Разрабатываемая программа должна обладать следующими
качествами:
-
Производить интегрирование заданной функции методом прямоугольников, трапеций, парабол на основе входных данных и выводить результат; -
Иметь графический интерфейс, позволяющий вводить исходные данные, а также визуализировать результаты вычислений, выводя на экран график подынтегральной функции, значения вычисленных интегралов и погрешности их вычислений. -
При написании исходных текстов программы необходимым условием является использование основных принципов объектно- ориентированного программирования, обработки исключительных ситуаций, потоков выполнения, наличие подключаемых библиотек.
 3. Алгоритм решения задачи
3. Алгоритм решения задачи
Данная курсовая работа посвящена разработке программы на языке C++, которая вычисляет определенный интеграл от функции, имеющей первообразную, которую можно вычислить с помощью той или иной приближённой формулы. Для решения задачи применяются методы прямоугольников, трапеций и парабол (Симпсона).
Задача курсового проекта – разработать программу на языке C++, такую, чтобы при работе с этой программой пользователь имел возможность:
-
Найти определенный интеграл выше упомянутыми методами от следующей функции:
б) увидеть на экране результаты вычислений интеграла от заданной функции

Ход работы
-
Метод правых и левых прямоугольников
Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под
графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах.
Если отрезок [a;b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по следующим формулам:
b
a
Формула правых прямоугольников:
f x dx≈f a b-a .
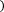
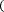
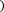
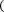
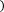
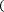
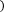
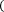
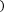 b
ba
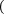
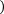 В случае разбиения отрезка интегрирования на n элементарных отрезков приведённые выше формулы применяются на каждом из этих элементарных отрезков между двумя соседними узлами. В результате, получаются составные квадратурные формулы:
В случае разбиения отрезка интегрирования на n элементарных отрезков приведённые выше формулы применяются на каждом из этих элементарных отрезков между двумя соседними узлами. В результате, получаются составные квадратурные формулы:-
Для левыхпрямоугольников:
b n=1
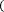
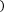
a i=0
f xi xi+1-xi .
-
Для правыхпрямоугольников:
b n
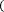
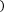
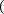
a i=0
f xi xi-xi-1 .
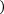
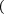
 Код программы для метода левых прямоугольников:
Код программы для метода левых прямоугольников:#include
{
setlocale(LC_ALL, "RUSSIAN"); double a, b, h, n, x, I;
cout<<"Введите нижний предел: " <<endl; cin>>a;
cout<<"Введитеверхнийпредел: " <<endl; cin>>b; cout<<endl; for (inti = 0; i <4;i++)
{
cout<<"Введите количество разбиений: "; cin>>n; h = (b - a) /n;
cout<<"Шаг: " <<h <<endl; x =a;
I =0;
for(inti = 0; i <n;i++)
{
I += (x*cos(x)); x += h;
}

I = I * h;
cout<<"Ответ: " <
}
return0;
}
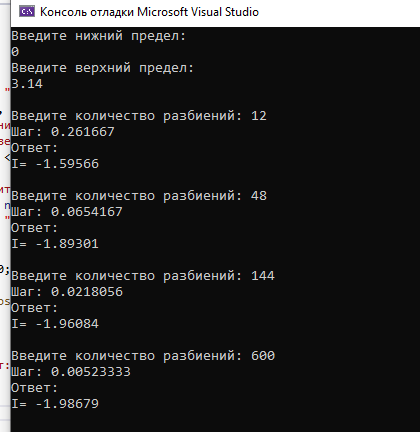 Результат выполнения программы (рисунок 2.1).
Результат выполнения программы (рисунок 2.1).Рисунок 2.1 – Метод левых прямоугольников Код программы для метода правых прямоугольников:
#include
{
setlocale(LC_ALL, "RUSSIAN"); double a, b, h, n, x, I;
cout<<"Введите нижний предел: " <<endl; cin>>a;
cout<<"Введитеверхнийпредел: " <<endl; cin>>b; cout<<endl; for (inti = 0; i <4;i++)
{
cout<<"Введите количество разбиений: "; cin>>n; h = (b - a) /n;
cout<<"Шаг: " <
I = 0;
for(inti = 0; i <n;i++)
{
I += (x * cos(x)); x += h;
}
I = I * h;

cout<<"Ответ: " <
}
return0;
}
Результат выполнения программы (рисунок 2.2).
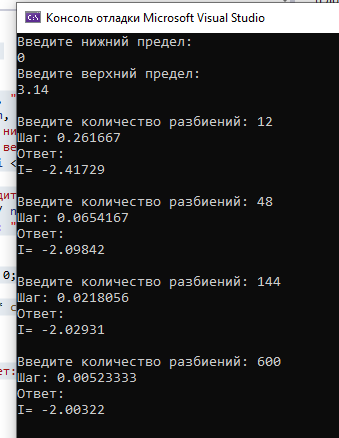
Рисунок 2.2 – Метод правых прямоугольников
-
Методтрапеций
Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную
функцию. Площадь под графиком функции аппроксимируется прямоугольнымитрапециями.



 Если отрезок [a;b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти поформуле:
Если отрезок [a;b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти поформуле:
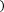 b
bf a +f b
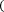
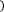
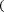
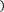
= b-a +E f ,
a 2
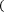
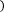
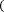
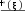 3
3E f =-
12
b-a .
 Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования).
Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования).Кодпрограммы:
#include
{
return(x * cos(x));
}
intmain()
{
setlocale(LC_ALL, "RUSSIAN"); double a, b, n, h, y, I;
cout<<"Введите нижний предел: " <<endl; cin>>a;
cout<<"Введитеверхнийпредел: " <<endl; cin>>b; cout<<endl; for (inti = 0; i <4;i++)
{
cout<<"Введите количество разбиений: "; cin>>n; h = (b - a) /n;
cout<<"Шаг: " <
for(inti = 1; i < n - 1;i++)
{
y += fun(a + h *i);
}
I = (((fun(a) + fun(b)) / 2) + y) * h; cout<<"I= " <<I <<endl<<endl;
}
return0;
}
Результат выполнения программы (рисунок 2.3).
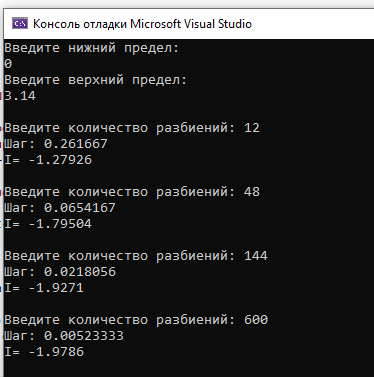
Рисунок 2.3 – Метод трапеций
-
МетодСимпсона
Суть метода заключается в приближении подынтегральной функции на отрезке [a;b] интерполяционным многочленом второй степени, то есть приближение графика функции на отрезке параболой.
 Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a;b]:
Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a;b]: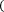
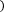 b b
b b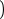
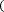
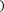 a α
a αp2 x dx=b-a
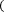
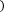 6
6f a +4f
a+b
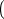 2
2+f(b) ,где
 f a ,f a+b
f a ,f a+b2
иf b -значенияфункциивсоответствующихточках(на
 концах отрезка и в его середине).
концах отрезка и в его середине).Кодпрограммы:
#include

{
return(x * cos(x));
}
intmain()
{
setlocale(LC_ALL, "RUSSIAN"); double a, b, h, n, y1, y2,I;
cout<<"Введите нижний предел: " <<endl; cin>>a;
cout<<"Введитеверхнийпредел: " <<endl; cin>>b; cout<<endl; for (inti = 0; i <4;i++)
{
cout<<"Введите количество разбиений: "; cin>>n; h = (b - a) /n;
cout<<"Шаг: " <
y1 = fun(a + h);
for(inti = 2; i <n; i +=2)
{
y1 += fun(a + (i + 1) * h); y2 += fun(a + i *h);
}
I = (fun(a) + 4 * y1 + 2 * y2) * h / 3; cout<<"I= " <<I <<endl<<endl;
}
return0;
}
Результат выполнения программы (рисунок 2.4).
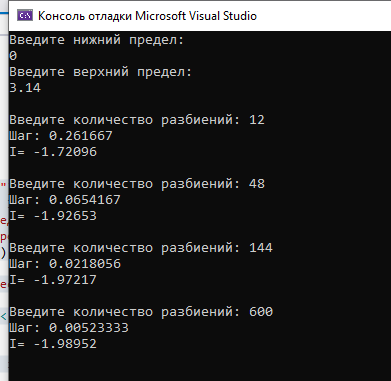
Рисунок 2.4 – Метод Симпсона
-
Метод трёхвосьмых
Метод основан на интерполяции функции на малом отрезке кубической параболой, проходящей через крайние и две равноотстоящие по "x" точки кривой f(x). Данный метод вычисляется по формуле:
b
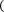
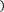
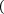
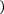


a 8
y0+y3n+2 y3+y6+…+yn-3 +3 y1+y2+…+yn-2+yn-1 ,
где h=b-a.
n
Код программы:
#include
{
return(x * cos(x));
}
intmain()
{
setlocale(LC_ALL, "RUSSIAN"); double a, b, h, I, n, y1,y2;
cout<<"Введите нижний предел: " <<endl; cin>>a;
cout<<"Введитеверхнийпредел: " <<endl; cin>>b; cout<<endl; for (inti = 0; i <4;i++)
{
cout<<"Введите количество разбиений: "; cin>>n; h = (b - a) /(n);
y1 = 0;
y2 = fun(a + h);
for(inti = 2; i <n;i++)
{
if(i % 3 == 0)
{
}
else
{
}
}
y1 += fun(a + i *h);
y2 += fun(a + (i * h));
 I = (fun(a) + fun(b) + 2 * y1 + 3 * y2) * 3 * h / 8; cout<<"I= " <<I <<endl<<endl;
I = (fun(a) + fun(b) + 2 * y1 + 3 * y2) * 3 * h / 8; cout<<"I= " <<I <<endl<<endl;}
return0;
}
Результат выполнения программы (рисунок 2.5).

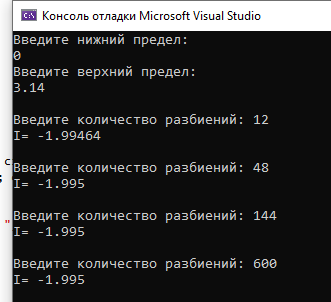
Рисунок 2.4 – Метод трёх восьмых
-
Результатывычислений
Результаты вычислений (таблица 2.1).
Таблица 2.1 – Результаты вычислений
| | n =12 | n = 48 | n =144 | n = 600 |
| Метод левых прямоугольников | -1.59566 | -1.89301 | -1.96084 | -1.98679 |
| Метод правых прямоугольников | -2.41729 | -2.09842 | -2.02931 | -2.00322 |
| Метод трапеций | -1.27926 | -1.79504 | -1.9271 | -1.9786 |
| Метод Симпсона | -1.72096 | -1.92653 | -1.97217 | -1.98952 |
| Метод трех восьмых | -1.99464 | -1.995 | -1.995 | -1.995 |

-
Заключение
В результате выполнения данной курсовой работы были получены навыки разработки программ, использующих в своей работе вычисление интеграла методами прямоугольников, Симпсона, трапеции и трех восьмых.
 Список используемых источников
Список используемых источников-
Язык программирования C++. Лекции и упражнения / С. Прата. – М.: ДиаСофт. – 2002. –896с. -
Рено Н.Н.: Численные методы. - М.: КДУ, 2007-182с. -
Qt. Профессиональное программирование на C++ : Наиболее полное руководство / М. Шлее. – СПб.: БХВ-Петербург, 2005. – 544с.
