Файл: Лекция 2_2.doc

В 1508 р. абат з Німеччини Йоганн Трисемус уперше описав застосування таблиць, що шифрують, заповненим алфавітом у випадковому порядку. Для одержання такого шифру заміни звичайно використовували таблицю для запису букв алфавіту та ключового слова (або фрази). У таблицю спочатку заносили по рядках ключове слово, причому букви, які повторюються, відкидалися. Потім ця таблиця доповнювалася буквами алфавіту, що ввійшли в неї з ключовим словом.

Оскільки ключове слово або фразу легко зберігати в пам'яті, то такий підхід спрощував процеси шифрування й розшифрування.

Розглянемо цей метод шифрування на прикладі. Для українського алфавіту таблиця, що шифрує, може мати розмір 48 (32 літери алфавіту). Виберемо як ключ слово “БАНДЕРОЛЬ”. Таблиця для шифрування має вигляд, поданий на рисунку 2.

Б	А	Н	Д	Е	Р	О	Л
Ь	В	Г	Є	Ж	З	И	І
Ї	Й	К	М	П	С	Т	У
Ф	Х	Ц	Ч	Ш	Щ	Ю	Я

Рисунок 2 – Таблиця для шифрування за методом Трисемуса з ключовим словом “БАНДЕРОЛЬ”

При шифруванні в таблиці знаходять чергову букву відкритого тексту й записують у шифротекст букву, розміщену нижче неї в тому самому стовпці. Якщо буква тексту виявляється в нижньому рядку таблиці, тоді для шифротексту беруть верхню букву з того самого стовпця.

Наприклад, при шифруванні за допомогою таблиці (рис. 2) повідомлення “МАГІСТРАЛЬ ЗРУЙНОВАНО”, одержимо шифротекст, записаний блоками по п’ять букв

ЧВКУЩ ЮЗВШЇ СЗЯХГ ИЙВГИ.

Такі табличні шифри називаються монограмними, тому що шифрування виконується по одній букві.

Криптографічний аналіз системи одноалфавітної заміни

Криптоаналіз системи одноалфавітної заміни, аналогічно шифру Цезаря, починається з підрахунку частот появи символів: визначається число появ кожної букви в шифротексті. Потім отриманий розподіл частот букв у шифротексті порівнюється з розподілом частот букв в алфавіті вихідних повідомлень, наприклад, в українському. Буква з найвищою частотою появи в шифротексті замінюється на букву з найвищою частотою появи в українській мові і т.д. Імовірність успішного розкриття системи шифрування підвищується зі збільшенням довжини шифротексту.

6 Біграмний шифр Плейфейра

Шифр Плейфейра (1854 р.), є найбільш відомим біграмним шифром заміни. Він застосовувався Великобританією під час Першої світової війни.

Основою шифру Плейфейра є таблиця, що шифрує, з випадково розміщеними буквами алфавіту вихідних повідомлень.

Для зручності запам'ятовування таблиці, що шифрує, відправник та одержувач повідомлень використовують ключове слово (або фразу) при заповненні початкових рядків таблиці. Загалом структура таблиці для шифрування системи Плейфейра повністю аналогічна структурі таблиці, що шифрує, Трисемуса. Тому для пояснення процедур шифрування й розшифрування в системі Плейфейра скористаємося таблицею шифрування Трисемуса (рис 2).

Процедура шифрування вміщує такі кроки:

Відкритий текст вихідного повідомлення розбивається на пари букв (біграми). Текст повинен мати парну кількість букв та не повинен містити біграми, що мають дві однакові букви. Якщо ці вимоги не виконані, то текст модифікується навіть через незначні орфографічні помилки.
Послідовність біграм відкритого тексту перетворюється за допомогою таблиці, що шифрує, у послідовність біграм шифротексту за такими правилами:

якщо обидві літери біграми відкритого тексту не стоять в одному рядку або стовпці, наприклад, літери А і П (рис. 2), тоді знаходять літери в кутах прямокутника, обумовленого вихідною парою літер. У нашому прикладі це букви АЙПЕ. Пара літер АП відображається в пару ЙЕ. Послідовність літер у біграмі шифротексту повинна бути дзеркально розміщеною щодо послідовності літер у біграмі відкритого тексту;
якщо обидві літери біграми відкритого тексту належать одному стовпцю таблиці, то за літери шифротексту беруть літери, які лежать під ними. Наприклад, біграма НК (рис 2) дає біграму шифротексту ГЦ. Якщо при цьому літера відкритого тексту стоїть в нижньому рядку, то для шифротексту береться відповідна літера з верхнього рядка того самого стовпця. Наприклад, біграма НЦ дає біграму шифротексту ГН;
якщо обидві літери біграми відкритого тексту належать одному рядку таблиці, то літерами шифротексту вважаються букви, які знаходяться праворуч від них. Наприклад, біграма НО дає біграму шифротексту ДЛ. Якщо при цьому літера відкритого тексту знаходиться в крайньому правому стовпці, то для шифру беруть відповідну літеру з лівого стовпця у тому самому рядку. Так біграма ЕЛ дає біграму шифротексту РБ).

Виконаємо зашифрування тексту

ВСЕ ТАЄМНЕ СТАЄ ЯВНИМ.

Розіб’ємо текст на біграми

ВС ЕТ АЄ МН ЕС ТА ЄЯ ВН ИМ.

Дана послідовність біграм відкритого тексту перетворюється за допомогою таблиці для шифрування (рис. 2) в таку послідовність біграм шифротексту:

ЗЙ ОП ДВ КД РП ЙО ІЧ ГА ЄТ.

При розшифруванні застосовується зворотний порядок дій.

Слід зазначити, що шифрування біграмами різко підвищує стійкість шифрів до розкриття.

7 Криптосистема Хілла

Алгебраїчний метод, що узагальнює афінну підстановку Цезаря:

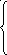для визначення n-грам, був сформульований Лестером С. Хіллом.

Множина цілих чисел , для яких визначені операції додавання, віднімання та множення за модулем m, є кільцем.

Множина всіх n-грам =(x₀, x₁, x₂, …, x_n-1) з компонентами кільця утворить векторний простір над кільцем . Кожна n-грама називається вектором. У векторному просторі для векторів визначені операції додавання та віднімання за модулем m, а також скалярне множення вектора на елемент t кільця . Додавання і скалярне множення є операціями, що задовольняють комутативний, асоціативний та дистрибутивний закони.

Вектор є лінійною комбінацією векторів , якщо

. (3.1)

Лінійне перетворення є відображенням

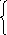, (3.2)

яке задовольняє умову лінійності

для всіх s, t та .

Лінійне перетворення може бути представлене матрицею розміром nn вигляду

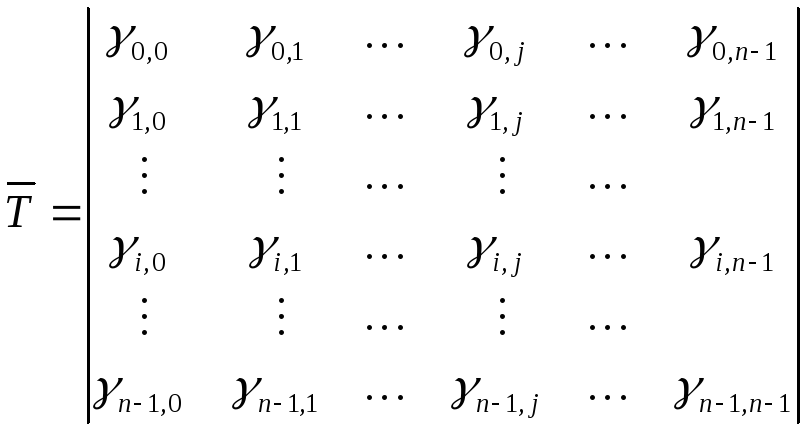, (3.3)

причому

або .

Базисом для векторного простору є набір векторів з , які лінійно незалежні і породжують . Кожен базис для містить n лінійно незалежних векторів. Довільний набір з n векторів, які лінійно незалежні над , є базисом.

Нехай є лінійним перетворенням, що описується матрицею (3.3), причому

Якщо вектори лінійно незалежні над , тоді їх образи лінійно незалежні над тільки в тому випадку, якщо визначник матриці не ділиться на будь-яке просте p, що ділить m. У цьому випадку перетворення називається невиродженим лінійним перетворенням, що має зворотне перетворення