ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 51
Скачиваний: 0
Традиційні симетричні криптосистеми Шифри простої заміни План
1 Полібіанський квадрат
2 Система шифрування Цезаря
3 Аффінна система підстановок Цезаря
4 Система Цезаря із ключовим словом
5 Таблиці Трисемуса
6 Біграмний шифр Плейфейра
7 Криптосистема Хілла
8 Система омофонів
Шифри простої заміни
При шифруванні заміною (підстановкою) символи тексту, що шифруються, замінюються символами того самого або іншого алфавіту із заздалегідь установленим правилом заміни. У шифрі простої заміни кожен символ вихідного тексту замінюється символами того самого алфавіту однаково протягом всього тексту. Часто шифри простої заміни називають шифрами одноалфавітної підстановки.
1 Полібіанський квадрат
Одним з перших шифрів простої заміни вважається так званий полібіанський квадрат. За два століття до нашої ери грецький письменник-історик Полібій винайшов для цілей шифрування квадратну таблицю розміром 55, заповнену буквами грецького алфавіту у випадковому порядку (рис. 1).
|
(лямбда) |
(ні) |
(тета) |
(сігма) |
(хі) |
|
(ро) |
(пі) |
(іпсилон) |
(альфа) |
(йота) |
|
(мі) |
(ета) |
(дельта) |
(фі) |
(гама) |
|
(псі) |
(ксі) |
(бета) |
(омега) |
(омікрон) |
|
(каппа) |
(епсилон) |
|
(дзета) |
(тау) |
Рисунок 1 – Полібіанський квадрат
При шифруванні в полібіанському квадраті знаходили букву відкритого тексту та записували в шифротекст букву, розміщену нижче у тому самому стовпці. Якщо буква відкритого тексту виявлялася в нижньому рядку таблиці, то для шифротексту брали верхню букву з того самого стовпця. Наприклад, для слова
одержимо такий шифротекст
Концепція полібіанського квадрата виявилася плідною і знайшла застосування в криптосистемах наступного часу.
2 Система шифрування Цезаря
Шифр Цезаря є окремим випадком шифру простої заміни (одноалфавітної підстановки). Шифр одержав свою назву від імені римського імператора Гая Юлія Цезаря, який використовував цей шифр при листуванні із Цицероном (близько 50 р. до н.е.).
При шифруванні вихідного
тексту кожна буква замінялася на іншу
букву того самого алфавіту за таким
правилом. Буква для підстановки
визначалася шляхом зсуву по алфавіту
від букви відкритого тексту на
![]() позицій.
При досягненні кінця алфавіту виконувався
циклічний перехід до його початку. Цезар
використав шифр із значенням K=3.
позицій.
При досягненні кінця алфавіту виконувався
циклічний перехід до його початку. Цезар
використав шифр із значенням K=3.
Наприклад, послання Цезаря ALEA JACTA EST («Жереб кинутий») для ключа K=3 у зашифрованому вигляді виглядає так: DOHD MDFWD HVW.
Таким чином, система Цезаря
являє собою одноалфавітну підстановку,
що шифрує n-граму
![]() відкритого тексту в n-граму
відкритого тексту в n-граму
![]() шифротексту відповідно до такого
правила:
шифротексту відповідно до такого
правила:
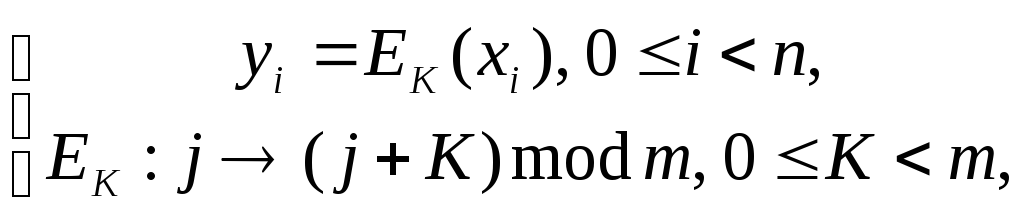
де
j – числовий код букви відкритого тексту;
![]() – числовий код відповідної букви
шифротексту.
– числовий код відповідної букви
шифротексту.
Система шифрування Цезаря
утворює сімейство одноалфавітних
підстановок для обраних значень ключа
![]() ,
причому
,
причому
![]() .
.
Перевагою системи шифрування Цезаря є простота шифрування та розшифрування.
До недоліків системи Цезаря необхідно віднести такі:
-
підстановки, що виконуються відповідно до системи Цезаря, не маскують частот появи букв вихідного відкритого тексту;
-
зберігається алфавітний порядок у послідовності букв, якими замінюються букви відкритого тексту; при зміні значення
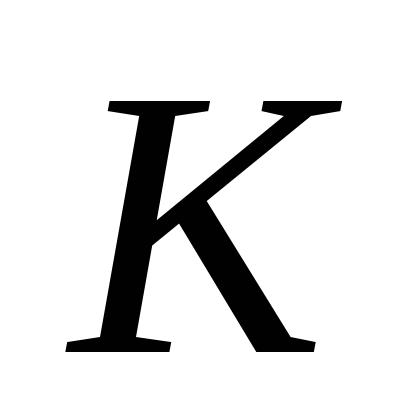 змінюються тільки початкові позиції
такої послідовності;
змінюються тільки початкові позиції
такої послідовності; -
число можливих ключів
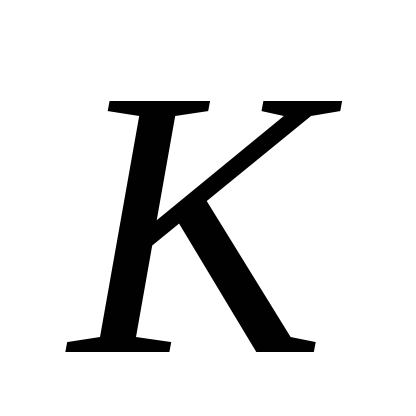 досить мале і обмежене кількістю букв
алфавіту;
досить мале і обмежене кількістю букв
алфавіту; -
шифр Цезаря легко розкривається на основі аналізу частот появи букв у шифротексті.
Криптоаналіз шифру Цезаря
Алгоритм злому шифру Цезаря можна виконати, використовуючи такий алгоритм:
-
Визначити частоти символів алфавіту. Занести їх у масив FiA.
-
Визначити частоти символів шифротексту. Занести їх у масив FiC:
а) обчислити скільки разів трапляється той або інший символ у шифротексті (занести в масив freq);
б) визначити кількість символів у шифротексті (l);
в) нормувати частоти символів, обчислені в пункті 2(a), результат помістити в масив FiC, тобто
![]() .
.
-
Знайти таке значення k, при якому сума одноіменних різниць d була б мінімальною:
а) обчислити для всіх значень k=0, 1, … , 26 суми різниць
![]() , де
, де
![]() ;
;
б) знайти мінімальну суму різниць d;
в) запам'ятати значення k.
-
Розшифрувати шифротекст, використовуючи ключ k.
Алгоритм, що розглянуто вище, можна застосовувати до текстів англійської мови. Це пояснюється тим, що процес аналізу шифротексту виконувався за модулем 27 (26 літер латинського алфавіту та пропуск). У випадку аналізу шифрів інших мов необхідно змінити в залежності від кількості літер в алфавіті, що розглядається, значення модуля, за яким ведеться аналіз.
3 Аффінна система підстановок Цезаря
У системі шифрування Цезаря
використовувалися тільки адитивні
властивості множини цілих чисел
![]() .
Однак елементи множини
.
Однак елементи множини
![]() можна
також множити за модулем m.
Застосовуючи одночасно операції
додавання та множення за модулем m
над елементами множини
можна
також множити за модулем m.
Застосовуючи одночасно операції
додавання та множення за модулем m
над елементами множини
![]() ,
можна одержати систему підстановок,
яку називають аффінною
системою підстановок Цезаря.
,
можна одержати систему підстановок,
яку називають аффінною
системою підстановок Цезаря.
Визначимо перетворення в такій системі:
![]()
![]()
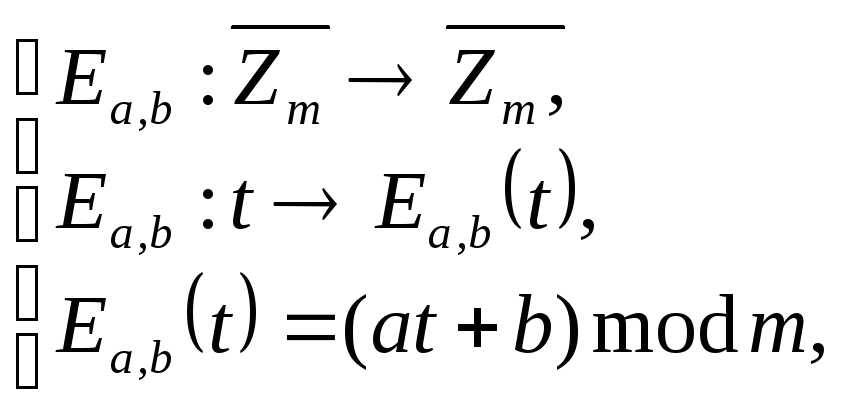
де
![]() ,
0
a<m, 0
b<m ,
,
0
a<m, 0
b<m ,
![]() .
.
У такому перетворенні літера, що відповідає числу t, замінюється літерою, що відповідає числовому значенню (at+b) за модулем m.
Слід помітити, що перетворення
![]() є взаємно однозначним відображенням
на множині
є взаємно однозначним відображенням
на множині
![]() тільки
в тому випадку, якщо числа а
та m є
взаємно простими.
тільки
в тому випадку, якщо числа а
та m є
взаємно простими.
Наприклад, візьмемо m = 26 (літери англійського алфавіту), а = 3, b = 5. Видно, НСД (3,26)=1. Отримаємо таку відповідність між числовими кодами букв:
|
T |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
3t+5 |
5 |
8 |
11 |
14 |
17 |
20 |
23 |
0 |
3 |
6 |
9 |
12 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
3t+5 |
18 |
21 |
24 |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
2 |

