Файл: Техническая термодинамика цели и задачи. Основные понятия и определения рабочее тело, термодинамическая система (тдс), виды тдс.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 72
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
19.Холодильная машина
Осуществим цикл Карно в обратном направлении. Рабочее тело с начальными параметрами точки а расширяется адиабатно, совершая работу расширения за счет внутренней энергии, и охлаждается от температуры Т1 до температуры T2 Дальнейшее расширение происходит по изотерме, и рабочее тело отбирает от нижнего источника с температурой T2 теплоту q2. Далее газ подвергается сжатию сначала по адиабате, и его температура от Т2повышается до T1, а затем — по изотерме (T1=const). При этом рабочее тело отдает верхнему источнику с температурой T1количество теплоты q1.
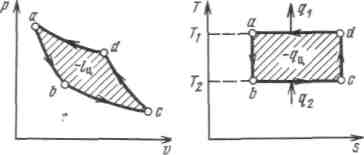
Рисунок 4.4 - Обратный цикл Карно в р,v- и T, s-диаграммах
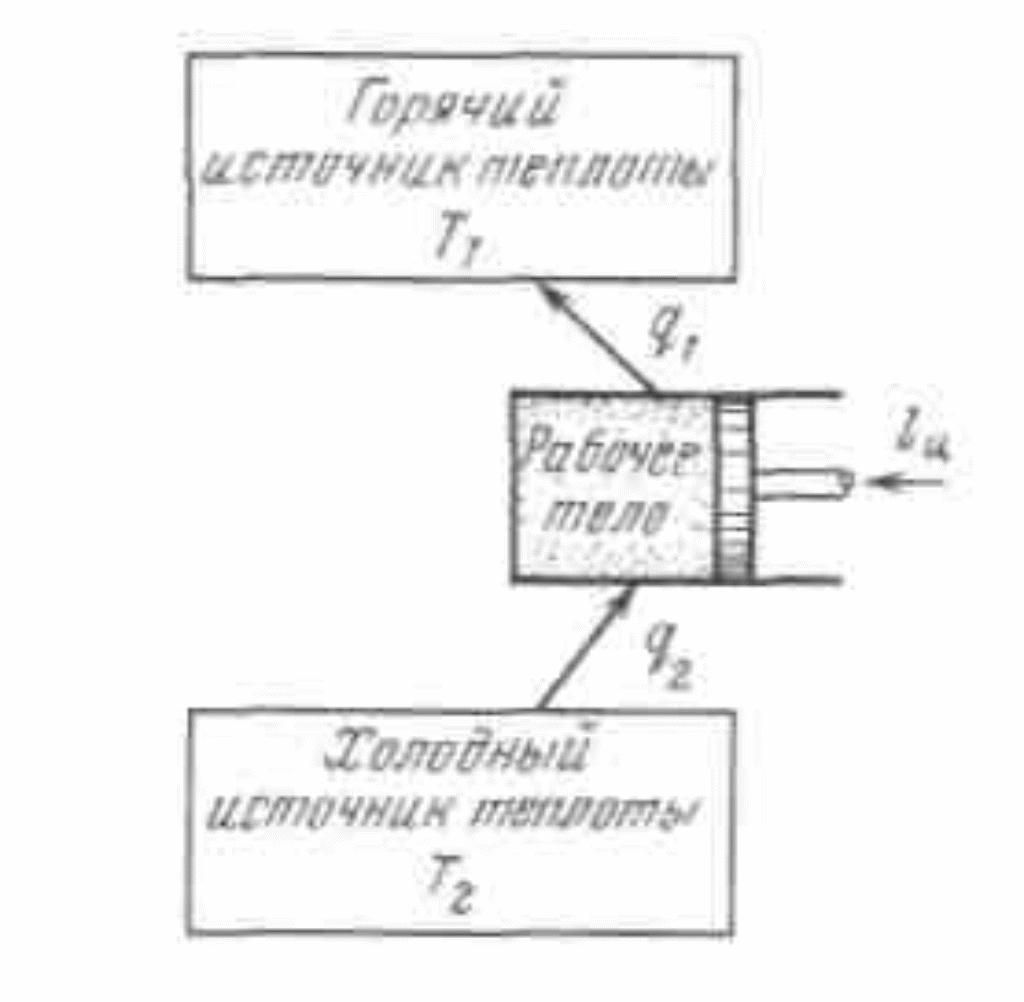
Рисунок 4.5 - Термодинамическая схема холодильной машины
Поскольку в обратном цикле сжатие рабочего тела происходит при более высокой температуре, чем расширение, работа сжатия, совершаемая внешними силами, больше работы расширения на величину площади abcd, ограниченной контуром цикла. Эта работа превращается в теплоту и вместе с теплотой q2 передается верхнему источнику. Таким образом, затратив на осуществление обратного цикла работу lц, можно перенести теплоту от источника с низкой температурой к источнику с более высокой температурой, при этом нижний источник отдаст количество теплоты q2, а верхний получит количество теплоты ql=q2lц.
Обратный цикл Карно является идеальным циклом холодильных установок и так называемых тепловых насосов.
В холодильной установке рабочими телами служат, как правило, пары легкокипящих жидкостей — фреона, аммиака и т.п. Процесс «перекачки теплоты» от тел, помещенных в холодильную камеру,
к окружающей среде происходит за счет затрат электроэнергии.
Эффективность холодильной установки оценивается холодильным коэффициентом, определяемым как отношение количества теплоты, отнятой за цикл от холодильной камеры, к затраченной в цикле работе:
Для обратного цикла Карно
Заметим, что чем меньше разность температур между холодильной камерой и окружающей средой, тем меньше нужно затратить энергии для передачи теплоты от холодного тела к горячему и тем выше холодильный коэффициент.
Холодильную установку можно использовать в качестве теплового насоса. Если, например, для отопления помещения использовать электронагревательные приборы, то количество теплоты, выделенное в них, будет равно расходу электроэнергии. Если же это количество электроэнергии использовать в холодильной установке, горячим источником, т. е. приемником теплоты,в которой является отапливаемое помещение, а холодным — наружная атмосфера, то количество теплоты, полученное помещением,
где q2— количество теплоты, взятое от наружной атмосферы, а
20.Адиабатный процесс.
Процесс, происходящий без теплообмена с окружающей средой, называется адиабатным, т. е.
ратуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа. Как правило, это возможно, ибо теплообмен происходит значительно медленнее, чем сжатие или расширение газа.
Уравнения первого закона термодинамика для адиабатного процесса принимают вид:
Интегрируя последнее уравнение при условии, что k =cp/cv=const, находим
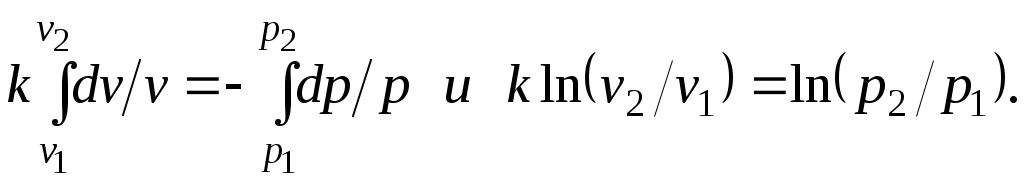
После потенцирования имеем
Это и есть уравнения адиабаты идеального газа при постоянном отношении теплоемкостей (k= const). Величина
называется показателемадиабаты. Подставив cp = cv-R, получим k. Согласно классической кинетической теории теплоемкость газов не зависит от температуры, поэтому можно считать, что величина kтакже не зависит от температуры и определяется числом степеней свободы молекулы. Для одноатомного газа k=1,66 для двухатомного k=1,4, для трех- и многоатомных газов k=l,33.
Поскольку k>1, то в координатах р,vлиния адиабаты идет круче линии изотермы: при адиабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.
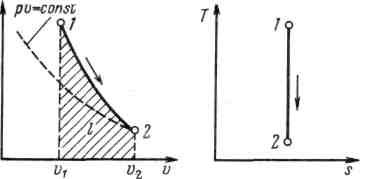
Рисунок 5.4 - Изображение адиабатного процесса в р, v- и Т, s-координатах
Определив из уравнения состояния, написанного для состояний 1и 2, отношение объемов или давлений, получим уравнение адиабатного процесса в форме, выражающей зависимость температуры от объема или давления:
;
Работа расширения при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по одной из следующих формул:
Так как
В данном процессе теплообмен газа с окружающей средой исключается, поэтому q=0. Выражение
Поскольку при адиабатном процессе
21. Изотермический процесс.
При изотермическом процессе температура постоянна, следовательно, pv = RT = const, или
т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении — падает (закон Бойля — Мариотта, 1662 г.).
Графиком изотермического процесса в р,v–координатах является равнобокая гипербола, для которой координатные оси служат асимптотами .
Работа процесса:
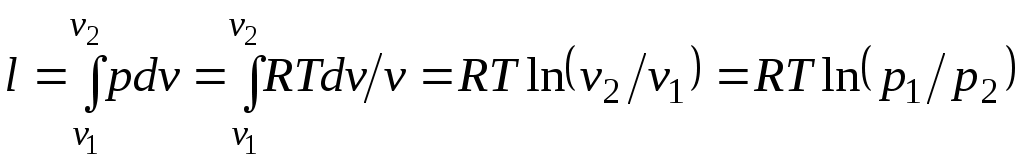 .
.Так как температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (
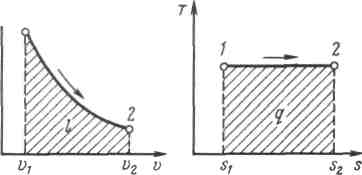
Рисунок 5.3 - Изображение изотермического процесса в р, v- и T, s-координатах.
При изотермическом сжатии от газа отводится теплота в количестве, равном затраченной на сжатие работе.
Изменение энтропии в изотермическом процессе выражается формулой
22. Изобарный процесс.
Из уравнения состояния идеального газа при р=const находим
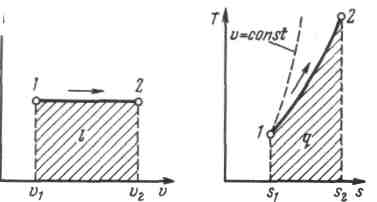
Рисунок 5.2 - Изображение изобарного процесса в p,v- и T,s-координатах
Из выражения
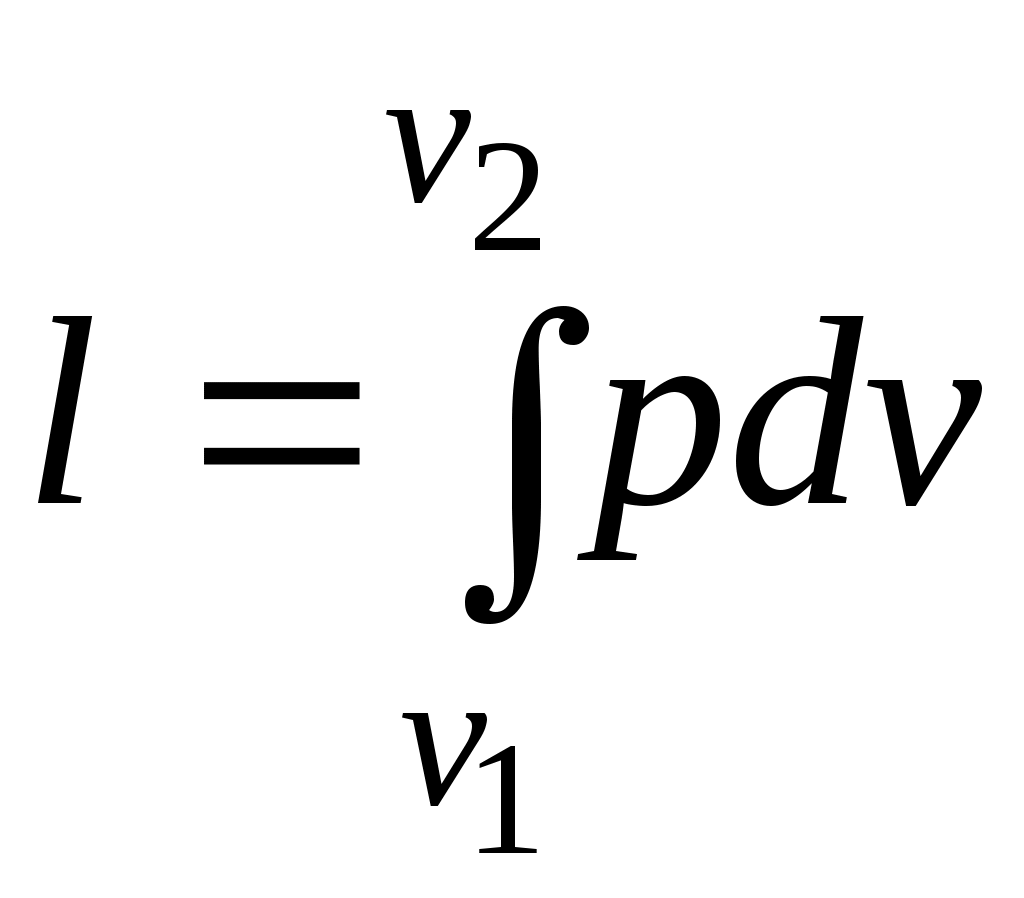 следует, что
следует, что Так как
Количество теплоты, сообщаемое газу при нагревании (или отдаваемое им при охлаждении):
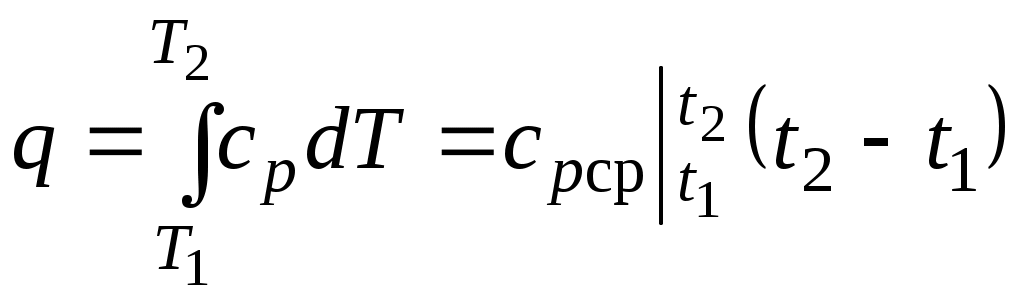 ,
,где
Изменение энтропии при ср = const согласно равно
