Файл: Техническая термодинамика цели и задачи. Основные понятия и определения рабочее тело, термодинамическая система (тдс), виды тдс.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 84
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,
т. е. температурная зависимость энтропии при изобарном процессе тоже имеет логарифмический характер, но поскольку ср>сv, то изобара в Т,s-диаграмме идет более полого, чем изохора.
23. Политропный процесс.
Любой произвольный процесс можно описать в р,v-координатах (по крайней мере на небольшом участке) уравнением
,
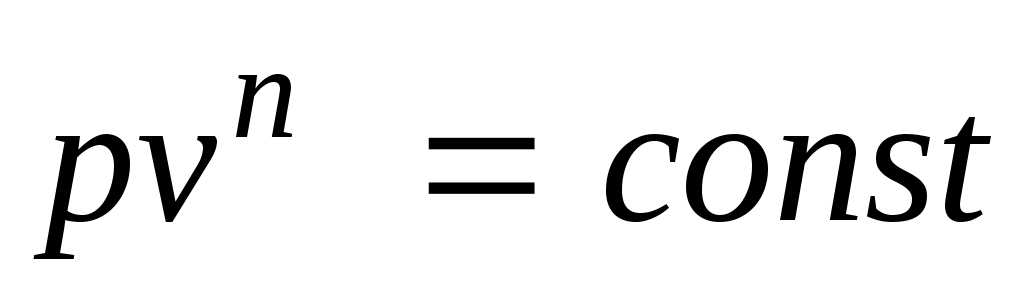подбирая соответствующее значение п. Процесс, описываемый таким уравнением, называется политропным. Показатель политропы n может принимать любое численное значение в пределах от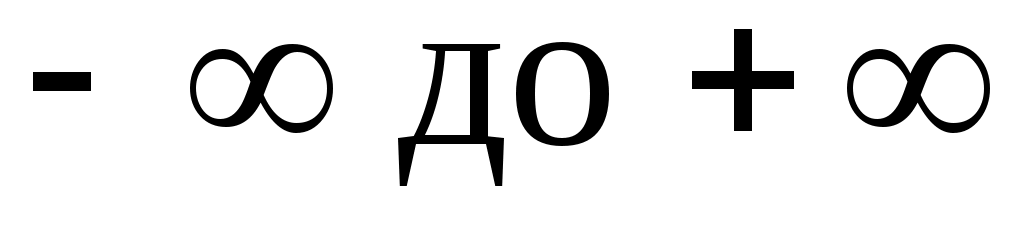
, но для данного процесса он является величиной постоянной.
Из уравнения Клапейрона нетрудно получить выражения, устанавливающие связь между р, vи Т в любых двух точках на политропе, аналогично тому, как это было сделано для адиабаты:
; 
; 
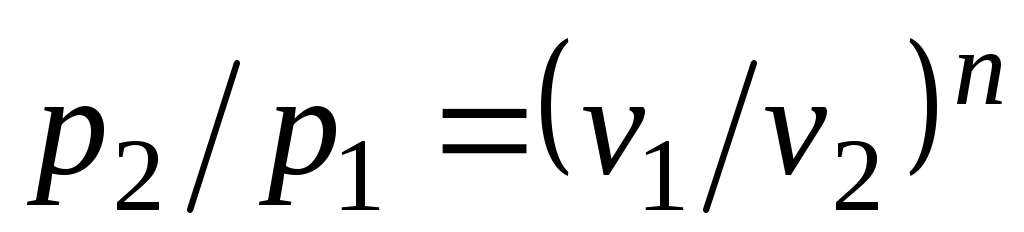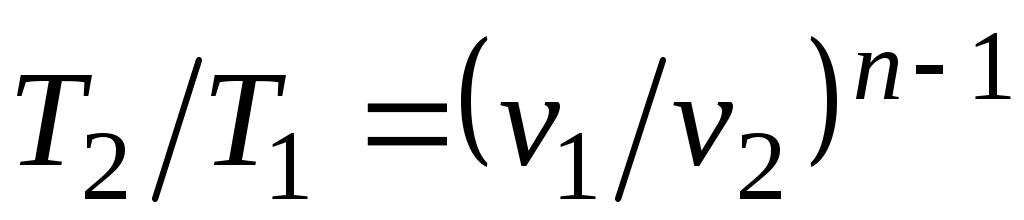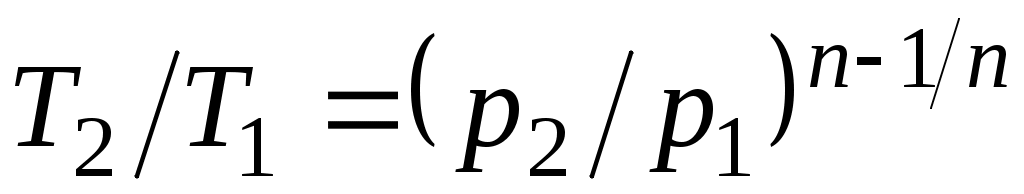. (5.1)
Работа расширения газа в политропном процессе имеет вид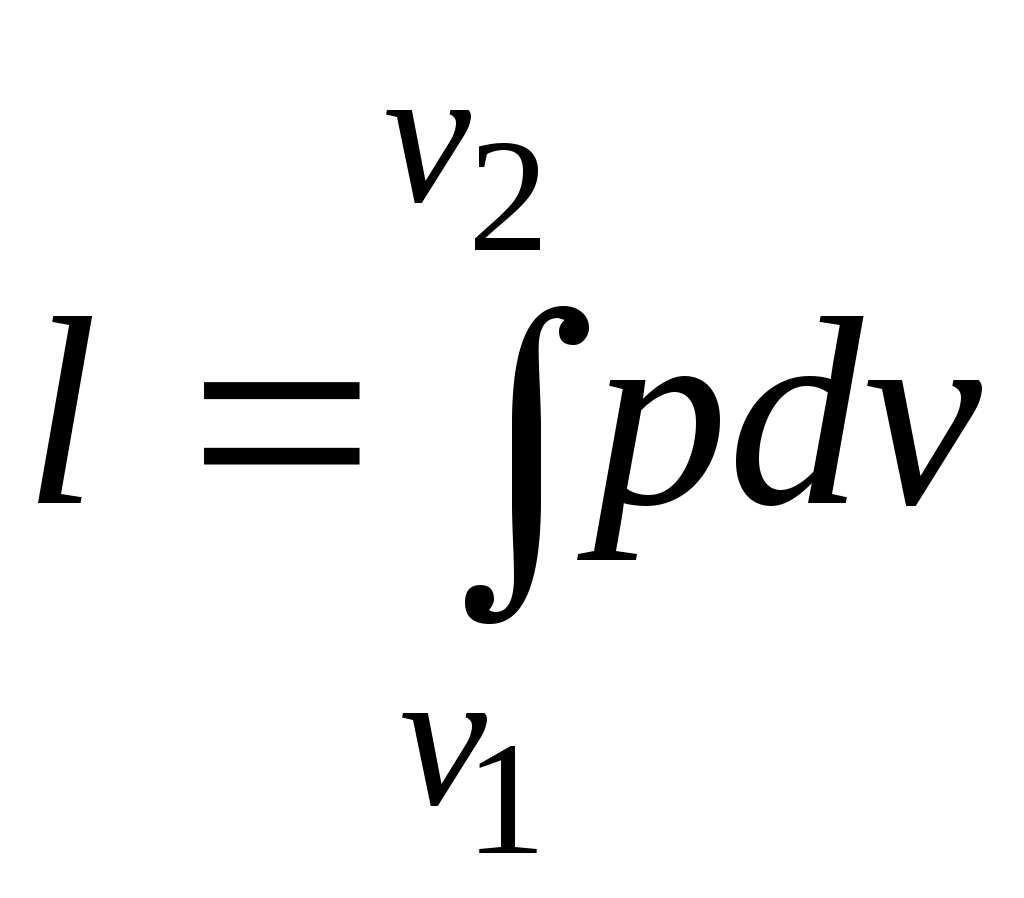
.
,
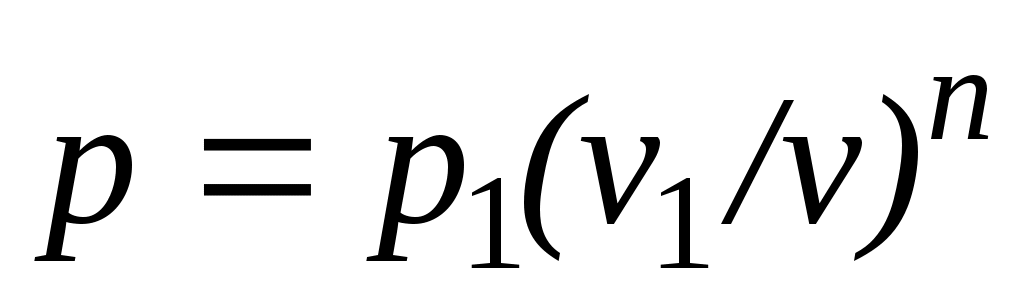то
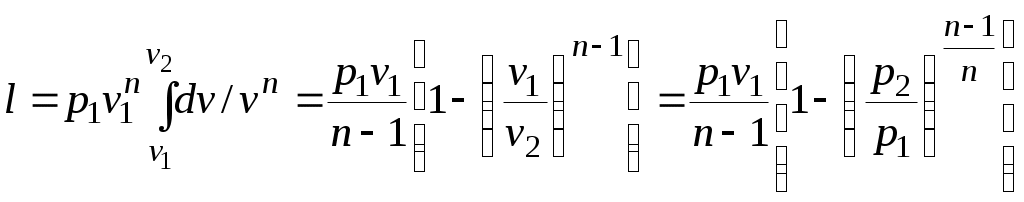(5.2)
Уравнение (5.1) можно преобразовать к виду:
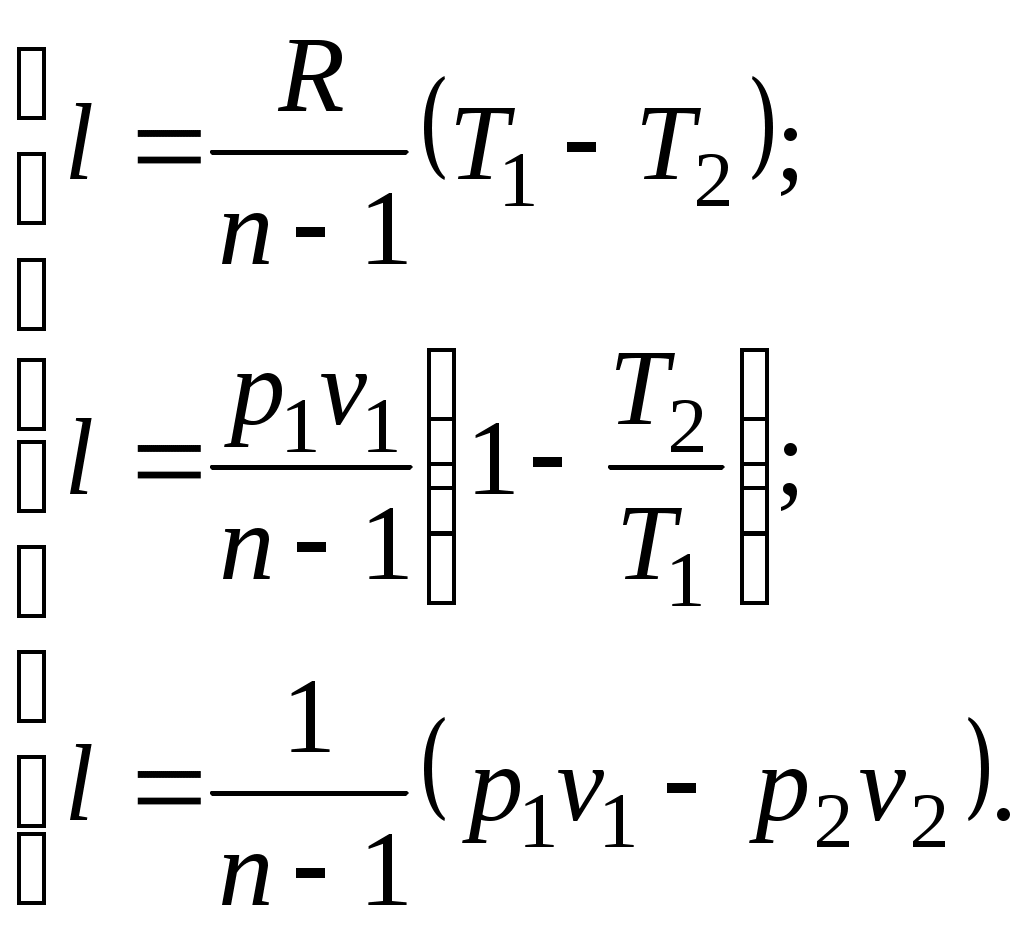
Количество подведенной (или отведенной) в процессе теплоты можно определить с помощью уравнения первого закона термодинамики: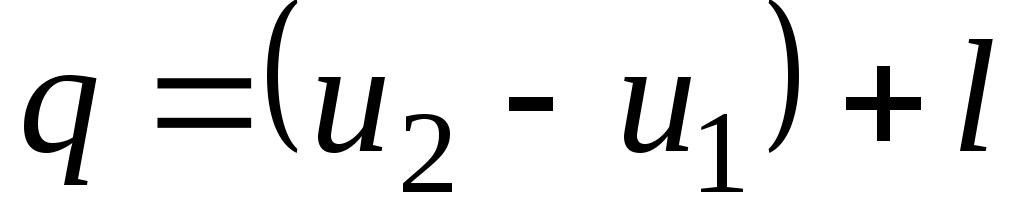
.
Поскольку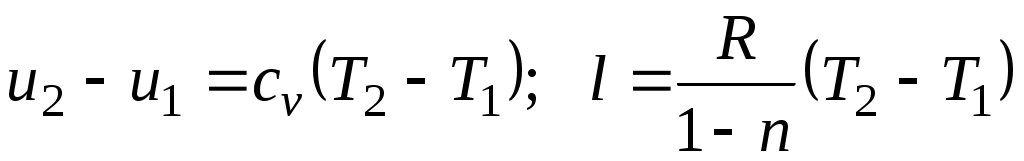
, то
,
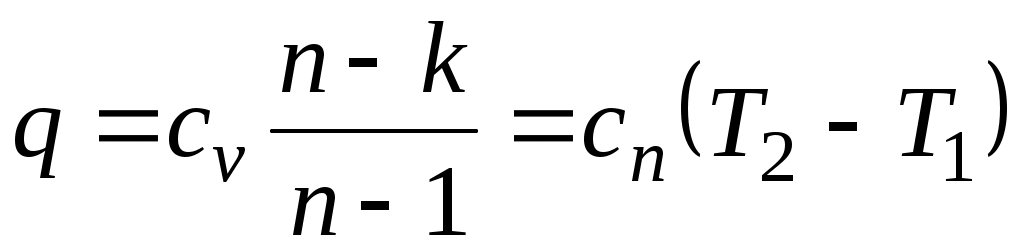где
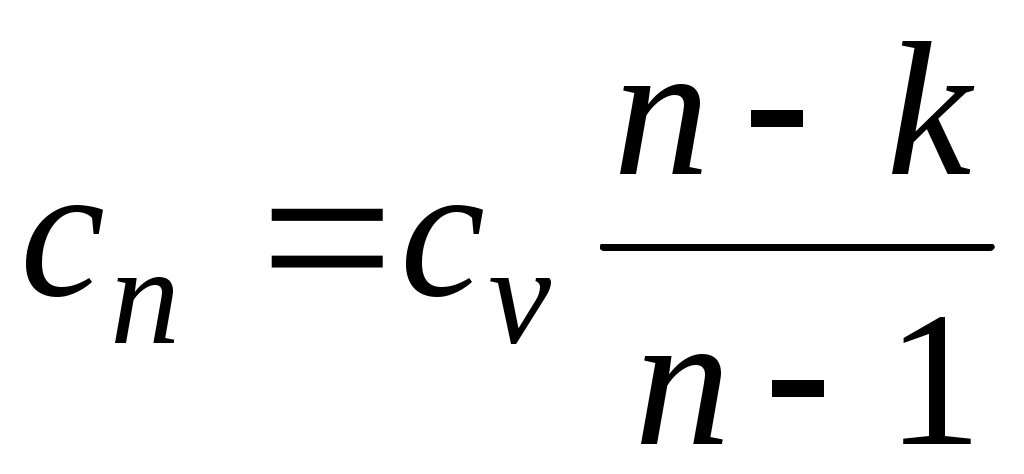
представляет собой теплоемкость идеального газа в политропном процессе. При постоянных cv, kи п теплоемкость сn = const, поэтому политропный процесс иногда определяют как процесс с постоянной теплоемкостью.
Изменение энтропии
.
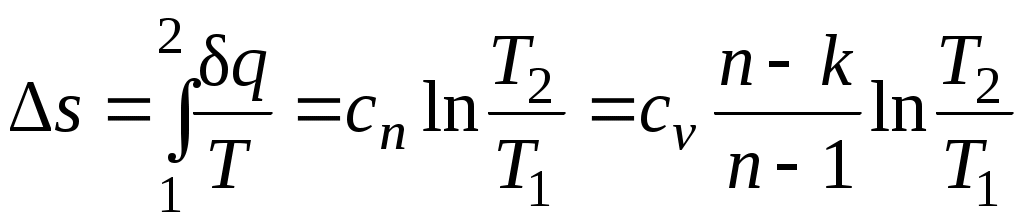Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов. Ниже приведены характеристики термодинамических процессов.
На рисунке показано взаимное распо
ложение на р, V- и Т, s-диаграммах политропных процессов с разными значениями показателя политропы. Все процессы начинаются в одной точке («в центре»).
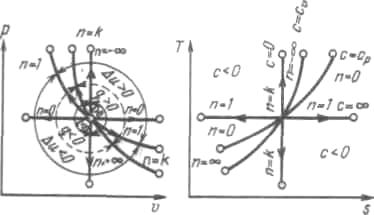
Рисунок 5.5 - Изображение основных термодинамических процессов идеального газа в р, v- и Т, s-координатах
Изохора (п= ±
) делит поле диаграммы на две области: процессы, находящиеся правее изохоры, характеризуются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных левее изохоры, характерна отрицательная работа.
Процессы, расположенные правее и выше адиабаты, идут с подводом теплоты к рабочему телу; процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты.
Для процессов, расположенных над изотермой ( = 1), характерно увеличение внутренней энергии газа; процессы, расположенные под изотермой, сопровождаются уменьшением внутренней энергии.
Процессы, расположенные между адиабатой и изотермой, имеют отрицательную теплоемкость, так как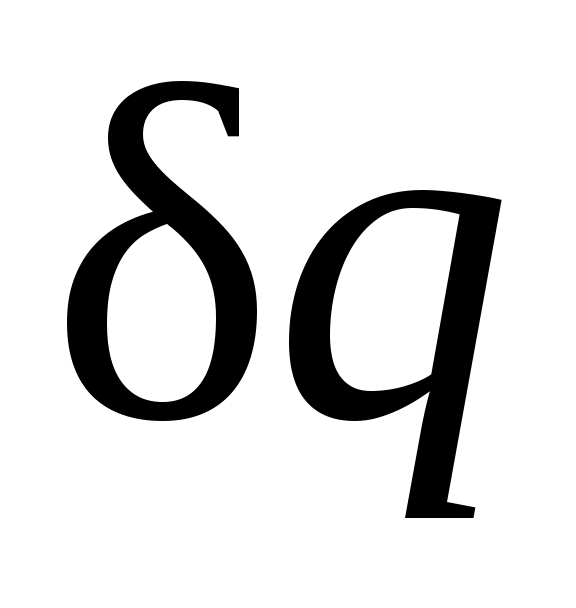
и du(а следовательно, и dT), имеют в этой области противоположные знаки. В таких процессах 
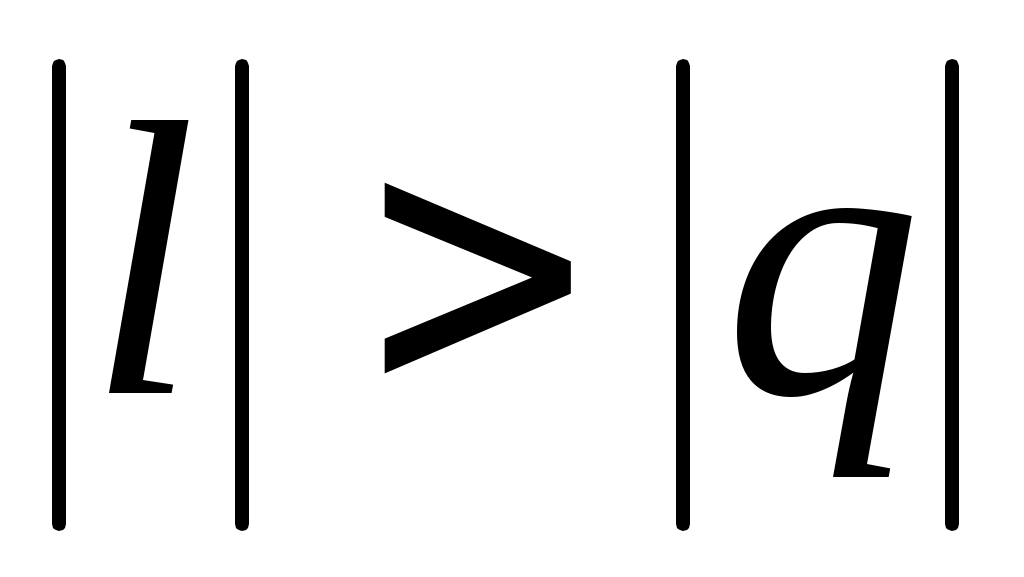, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела.
24. Изохорный процесс.
При изохорном процессе выполняется условие
dv = 0 или v= const. Из уравнения состояния идеального газа следует, что p/T=R/v=const, т. е. давление газа прямо пропорционально его абсолютной температуре:
.
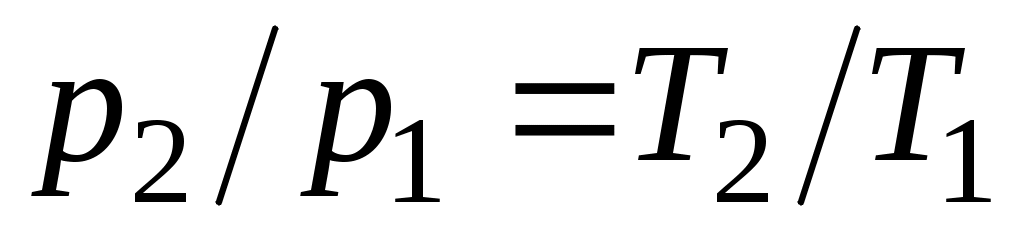Рисунок 5.1 - Изображение изохорного процесса в р,v- и T, s-координатах
Работа расширения в этом процессе равна нулю, так как dv= 0.
Количество теплоты, подведенной к рабочему телу в процессе
12 при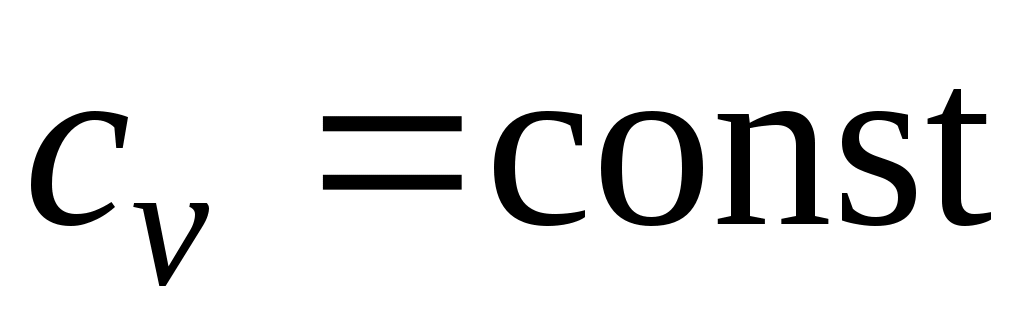
, определяется как:
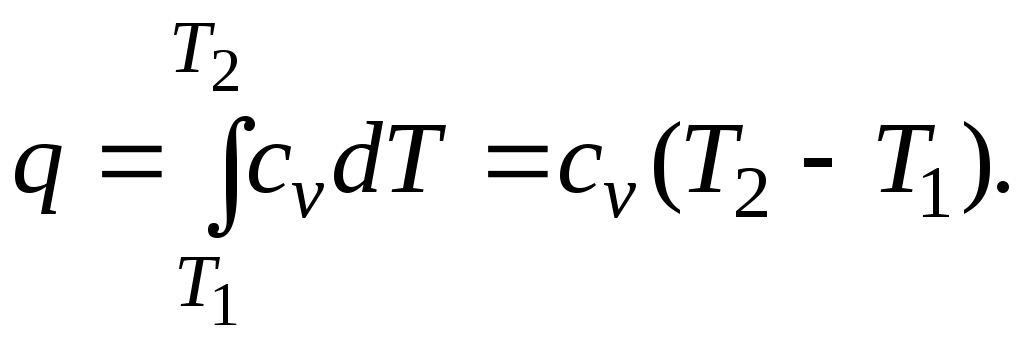
При переменной теплоемкости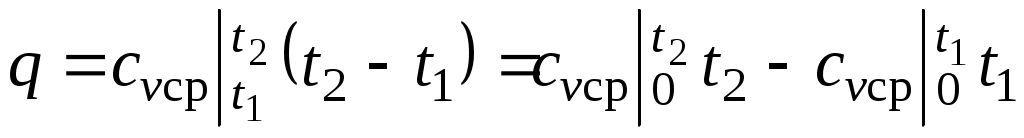
, где 
— средняя массовая изохорная теплоемкость в интервале температур от t1 до t2.
Так как 1= 0, то в соответствии с первым законом термодинамик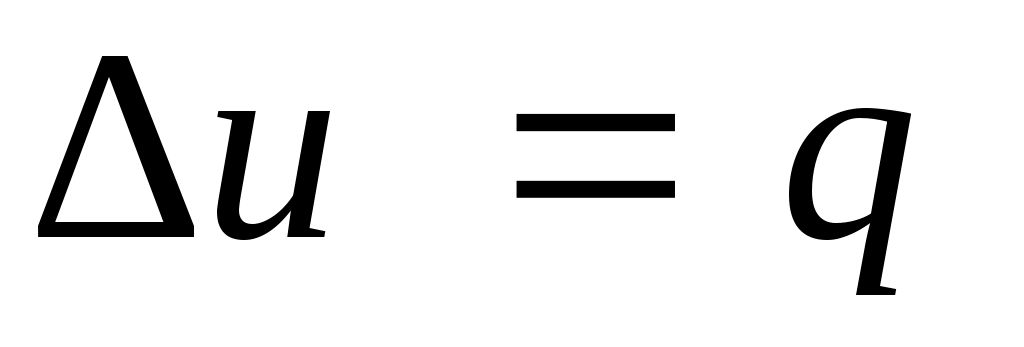и
и
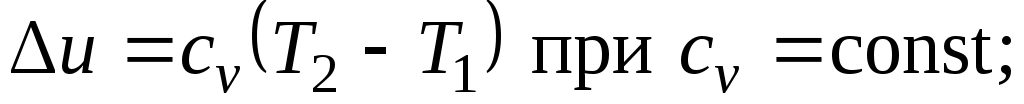
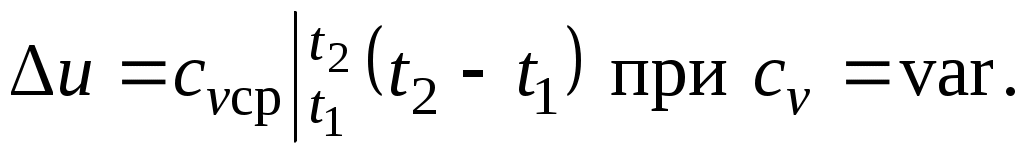
Поскольку внутренняя энергия идеального газа является функцией только его температуры, то полученные формулы справедливы для любого термодинамического процесса идеального газа.
Изменение энтропии в изохорном процессе определяется по формуле
,
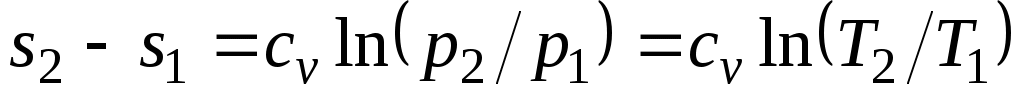т. е. зависимость энтропии от температуры на изохоре при сv = const имеет логарифмический характер.
25. Водяной пар.
Пар – это реальный газ в состоянии, близком к жидкой фазе (насыщению).
Водяной пар широко используется в качестве рабочего тела в теплоэнергетических и в промышленных установках. Он производится в котельных агрегатах при заданном постоянном давлении. На рисунке 1 дана pv-диаграмма для водяного пара.
Р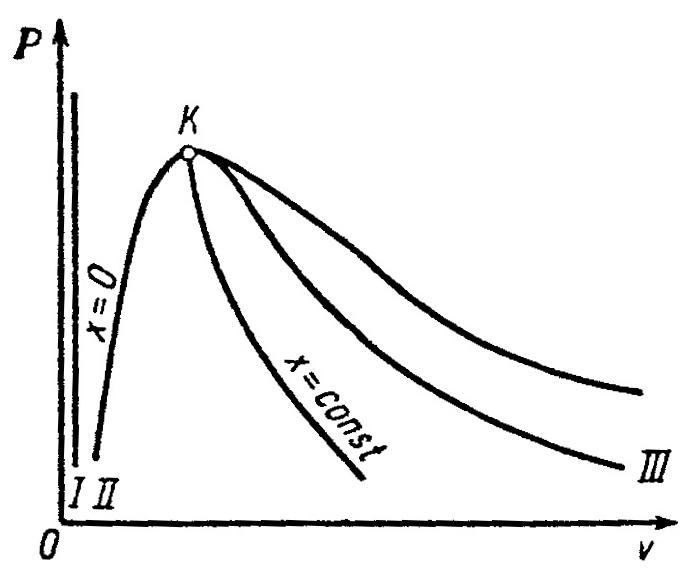
исунок 1 – PV-диаграмма для водяного пара
Кривая I- вода при 00С;
Кривая II- вода при температуре кипения (или температуре насыщения) – нижняя пограничная кривая;
Кривая III– сухой насыщенный пар – верхняя пограничная кривая.
Точка К– это критическая точка, разделяющая обе пограничные кривые.
Кривые I,II,IIIделят всю диаграмму на три части:
1) область между IиII– жидкость;
2) область между IIиIII– смесь кипящей жидкости и пара, т.е. влажный насыщенный пар;
3) область правее III– перегретый пар.
Критическая точка К характеризует критическое состояние, при котором исчезает различие в свойствах пара и жидкости. Критическая температура является наивысшей температурой жидкости и её насыщенного пара. При температурах выше критической возможно существование только перегретого пара.
Критические параметры водяного пара: tкр=374,150С; ркр=22,129МПа;vкр=0,00326м3/кг.
26. T-S диаграмма водяного пара. Теплота парообразования
Ввиду сложности уравнений состояния для пара в расчетной практике они не применяются. Для практических целей используют таблицы термодинамических параметров состояния. Две таблицы составлены для определения теплофизических свойств насыщенной жидкости и сухого насыщенного пара, т.е. в них приведены: ts, ps, u¢, u², h¢, h², r, s¢, s². В качестве независимой переменной в первой из этих таблиц использована температура, а во второй - давление. В третьей таблице приведены u, h и s для недогретой до температуры насыщения воды и перегретого пара в широком диапазоне давлений и температур.
Параметры влажного пара могут быть рассчитаны по приведенным выше формулам с использованием параметров насыщенной жидкости и сухого пара, взятых из таблиц.
T, s-диаграмма водяного пара. Наряду с табличными данными в практических расчетах широко пользуются графическими методами решения задач. Для этих целей используют T, s и h, s - диаграммы для пара.
Рассмотрим диаграмму - T, s. Начальное состояние 1 кг воды при Т0 = 273 К и s0 = 0 изобразится точкой а (рис. 8.3), а в - изобара подогрева воды до температуры насыщения Ts. Точка в соответствует насыщенной жидкости, вс - процесс парообразования (кипения) при p = const и Ts = const. Следовательно, вс является одновременно изобарой и изотермой. Точка с соответствует сухому насыщенному пару. Любая точка между точками в и с (например точка г) будет соответствовать влажному насыщенному пару. Линия cd - изобара перегрева пара. Точка d соответствует перегретому пару. Линии ав и cd согласно уравнениям (8.7) и (8.24) являются логарифмическими кривыми.
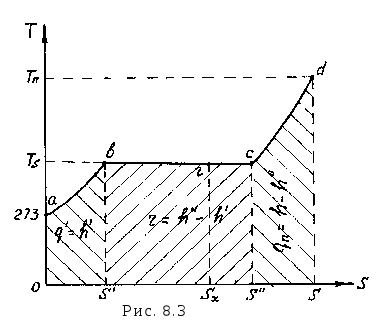
Площади под кривыми ав, вс и cd изображают соответственно теплоту жидкости q¢, теплоту парообразования r и теплоту перегрева пара qп. Из выражений (8.13) и (8.20) следует, что x = (sx - s¢)/(s² - s¢), т.е. х = вг / вс (рис. 8.3).
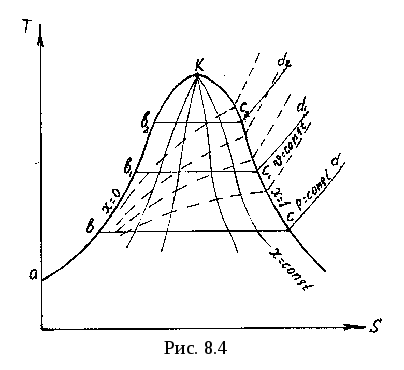
Таким образом, весь процесс парообразования от состояния воды при 0 оС до состояния перегретого пара с температурой Тп изображается изобарой авcd. При другом, более высоком давлении р
т. е. температурная зависимость энтропии при изобарном процессе тоже имеет логарифмический характер, но поскольку ср>сv, то изобара в Т,s-диаграмме идет более полого, чем изохора.
23. Политропный процесс.
Любой произвольный процесс можно описать в р,v-координатах (по крайней мере на небольшом участке) уравнением
, подбирая соответствующее значение п. Процесс, описываемый таким уравнением, называется политропным. Показатель политропы n может принимать любое численное значение в пределах от
, но для данного процесса он является величиной постоянной.Из уравнения Клапейрона нетрудно получить выражения, устанавливающие связь между р, vи Т в любых двух точках на политропе, аналогично тому, как это было сделано для адиабаты:
; ; . (5.1)Работа расширения газа в политропном процессе имеет вид
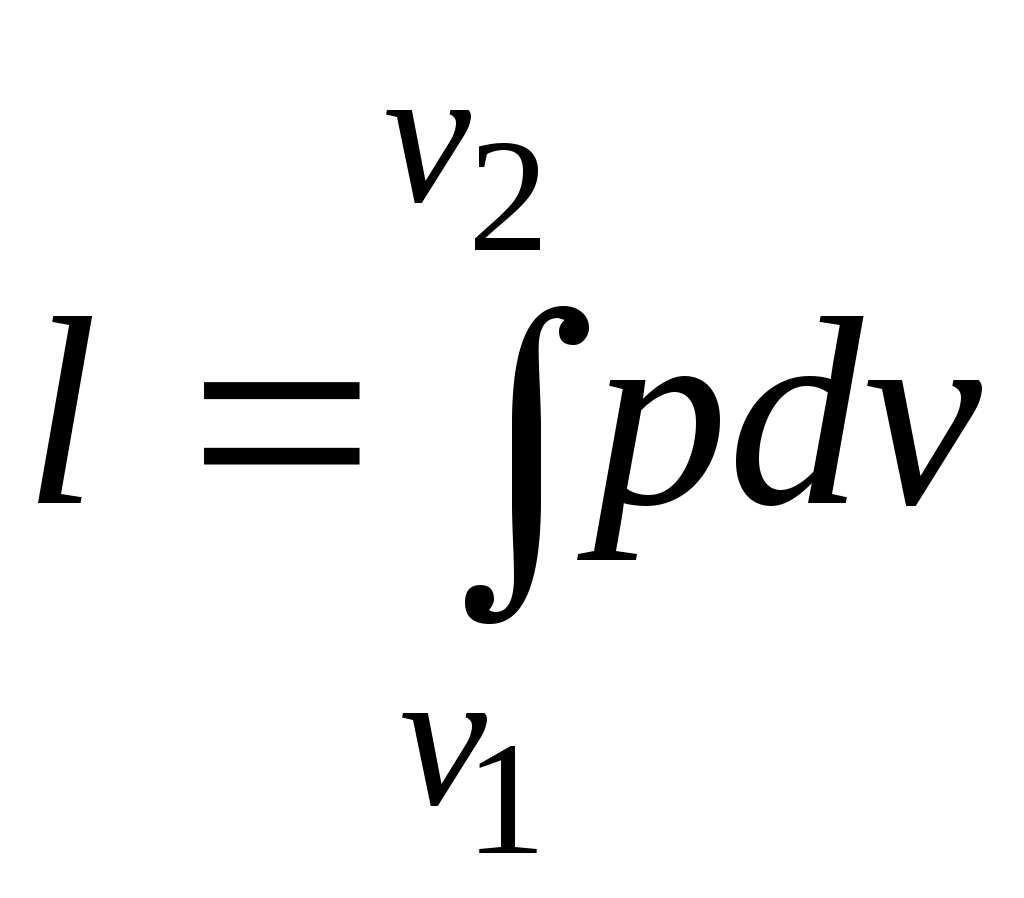.Так как для политропы в соответствии с (5.1)
,то
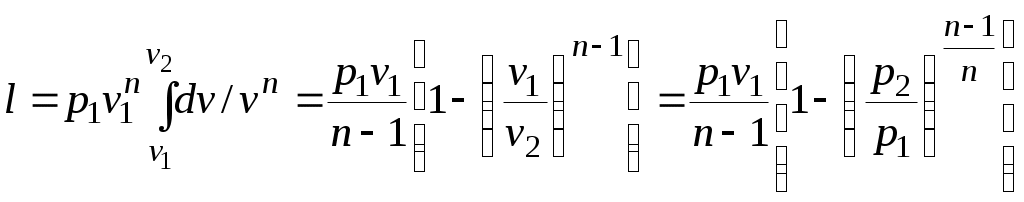(5.2)Уравнение (5.1) можно преобразовать к виду:
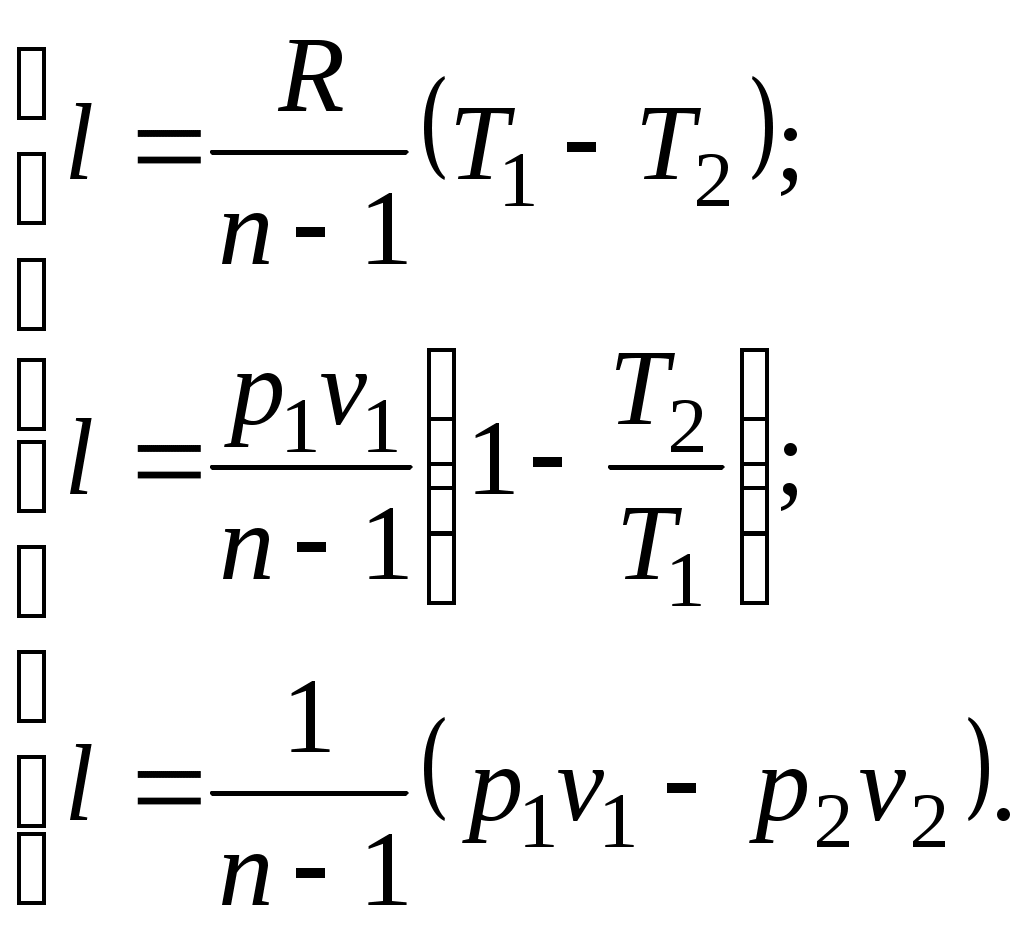
Количество подведенной (или отведенной) в процессе теплоты можно определить с помощью уравнения первого закона термодинамики:
.Поскольку
, то ,где
представляет собой теплоемкость идеального газа в политропном процессе. При постоянных cv, kи п теплоемкость сn = const, поэтому политропный процесс иногда определяют как процесс с постоянной теплоемкостью.
Изменение энтропии
.Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов. Ниже приведены характеристики термодинамических процессов.
| Процесс | п |  |
| Изохорный |  |  |
| Изобарный | 0 |  |
| Изотермический | 1 |  |
| Адиабатный | k | 0 |
На рисунке показано взаимное распо
ложение на р, V- и Т, s-диаграммах политропных процессов с разными значениями показателя политропы. Все процессы начинаются в одной точке («в центре»).
Рисунок 5.5 - Изображение основных термодинамических процессов идеального газа в р, v- и Т, s-координатах
Изохора (п= ±
) делит поле диаграммы на две области: процессы, находящиеся правее изохоры, характеризуются положительной работой, так как сопровождаются расширением рабочего тела; для процессов, расположенных левее изохоры, характерна отрицательная работа.Процессы, расположенные правее и выше адиабаты, идут с подводом теплоты к рабочему телу; процессы, лежащие левее и ниже адиабаты, протекают с отводом теплоты.
Для процессов, расположенных над изотермой ( = 1), характерно увеличение внутренней энергии газа; процессы, расположенные под изотермой, сопровождаются уменьшением внутренней энергии.
Процессы, расположенные между адиабатой и изотермой, имеют отрицательную теплоемкость, так как
и du(а следовательно, и dT), имеют в этой области противоположные знаки. В таких процессах , поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела. 24. Изохорный процесс.
При изохорном процессе выполняется условие
dv = 0 или v= const. Из уравнения состояния идеального газа следует, что p/T=R/v=const, т. е. давление газа прямо пропорционально его абсолютной температуре:
. Рисунок 5.1 - Изображение изохорного процесса в р,v- и T, s-координатах
Работа расширения в этом процессе равна нулю, так как dv= 0.
Количество теплоты, подведенной к рабочему телу в процессе
12 при
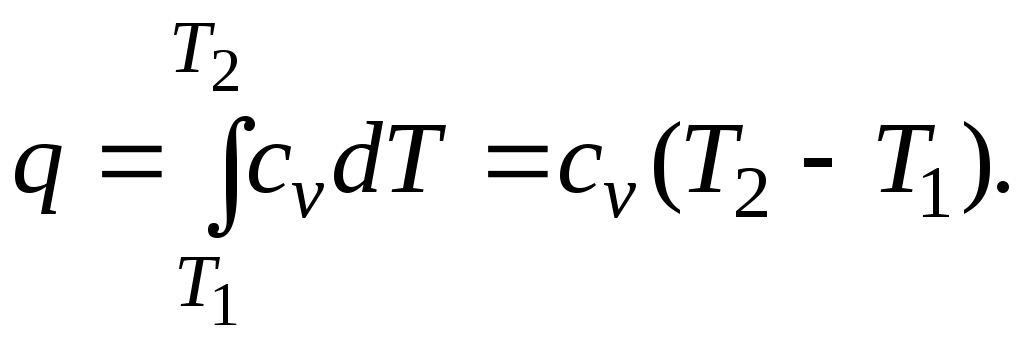
, определяется как: При переменной теплоемкости
, где — средняя массовая изохорная теплоемкость в интервале температур от t1 до t2.Так как 1= 0, то в соответствии с первым законом термодинамики
и Поскольку внутренняя энергия идеального газа является функцией только его температуры, то полученные формулы справедливы для любого термодинамического процесса идеального газа.
Изменение энтропии в изохорном процессе определяется по формуле
,т. е. зависимость энтропии от температуры на изохоре при сv = const имеет логарифмический характер.
25. Водяной пар.
Пар – это реальный газ в состоянии, близком к жидкой фазе (насыщению).
Водяной пар широко используется в качестве рабочего тела в теплоэнергетических и в промышленных установках. Он производится в котельных агрегатах при заданном постоянном давлении. На рисунке 1 дана pv-диаграмма для водяного пара.
Р
исунок 1 – PV-диаграмма для водяного параКривая I- вода при 00С;
Кривая II- вода при температуре кипения (или температуре насыщения) – нижняя пограничная кривая;
Кривая III– сухой насыщенный пар – верхняя пограничная кривая.
Точка К– это критическая точка, разделяющая обе пограничные кривые.
Кривые I,II,IIIделят всю диаграмму на три части:
1) область между IиII– жидкость;
2) область между IIиIII– смесь кипящей жидкости и пара, т.е. влажный насыщенный пар;
3) область правее III– перегретый пар.
Критическая точка К характеризует критическое состояние, при котором исчезает различие в свойствах пара и жидкости. Критическая температура является наивысшей температурой жидкости и её насыщенного пара. При температурах выше критической возможно существование только перегретого пара.
Критические параметры водяного пара: tкр=374,150С; ркр=22,129МПа;vкр=0,00326м3/кг.
26. T-S диаграмма водяного пара. Теплота парообразования
Ввиду сложности уравнений состояния для пара в расчетной практике они не применяются. Для практических целей используют таблицы термодинамических параметров состояния. Две таблицы составлены для определения теплофизических свойств насыщенной жидкости и сухого насыщенного пара, т.е. в них приведены: ts, ps, u¢, u², h¢, h², r, s¢, s². В качестве независимой переменной в первой из этих таблиц использована температура, а во второй - давление. В третьей таблице приведены u, h и s для недогретой до температуры насыщения воды и перегретого пара в широком диапазоне давлений и температур.
Параметры влажного пара могут быть рассчитаны по приведенным выше формулам с использованием параметров насыщенной жидкости и сухого пара, взятых из таблиц.
T, s-диаграмма водяного пара. Наряду с табличными данными в практических расчетах широко пользуются графическими методами решения задач. Для этих целей используют T, s и h, s - диаграммы для пара.
Рассмотрим диаграмму - T, s. Начальное состояние 1 кг воды при Т0 = 273 К и s0 = 0 изобразится точкой а (рис. 8.3), а в - изобара подогрева воды до температуры насыщения Ts. Точка в соответствует насыщенной жидкости, вс - процесс парообразования (кипения) при p = const и Ts = const. Следовательно, вс является одновременно изобарой и изотермой. Точка с соответствует сухому насыщенному пару. Любая точка между точками в и с (например точка г) будет соответствовать влажному насыщенному пару. Линия cd - изобара перегрева пара. Точка d соответствует перегретому пару. Линии ав и cd согласно уравнениям (8.7) и (8.24) являются логарифмическими кривыми.
Площади под кривыми ав, вс и cd изображают соответственно теплоту жидкости q¢, теплоту парообразования r и теплоту перегрева пара qп. Из выражений (8.13) и (8.20) следует, что x = (sx - s¢)/(s² - s¢), т.е. х = вг / вс (рис. 8.3).
Таким образом, весь процесс парообразования от состояния воды при 0 оС до состояния перегретого пара с температурой Тп изображается изобарой авcd. При другом, более высоком давлении р