Файл: Техническая термодинамика цели и задачи. Основные понятия и определения рабочее тело, термодинамическая система (тдс), виды тдс.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 81
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 весь процесс изобразится линией ав1с1d1 (рис. 8.4), при давлении p2 > р1 - линией ав2с2d2 и т.д. При увеличении давления точки в и с сближаются. Соединив между собой точки в, в1, в2 ... и т.д., получим линию насыщенной жидкости или нижнюю пограничную кривую. Строго говоря, линии подогрева жидкости ав, ав1, ав2 и т.д. не совпадают, но различие между ними очень невелико и практически они сливаются в одну линию, поэтому можно считать, что пограничная кривая совпадает с линиями подогрева жидкости до Ts при различных давлениях.
Соединяя точки с, с1, с2 ... и т.д., получим линию сухого насыщенного пара или верхнюю пограничную кривую. Точка соединения верхней и нижней пограничных кривых дает критическую точку к. Между пограничными кривыми лежит область влажного насыщенного пара. Правее и выше верхней пограничной кривой кс будет перегретый пар, а часть диаграммы, лежащая левее нижней пограничной кривой, ак будет областью жидкости. В области влажного пара наносят линии постоянной степени сухости x = const. На диаграмму также наносятся изохоры u = const.
Некоторым неудобством данной диаграммы является то, что при определении количества теплоты приходится измерять соответствующие площади.
Диаграмма h. s для водяного пара. Более удобной для расчетных целей является диаграмма h, s (диаграмма Молье). Одним из ее основных преимуществ перед T, s - диаграммой является то, что количество теплоты, участвующее в процессе, изображается линейным отрезком, а не площадью, как в системе координат T, s.
По значениям h¢, s¢, h², s², взятым из таблиц для разных давлений, строят верхнюю КВ и нижнюю ОК пограничные кривые (рис. 8.5).
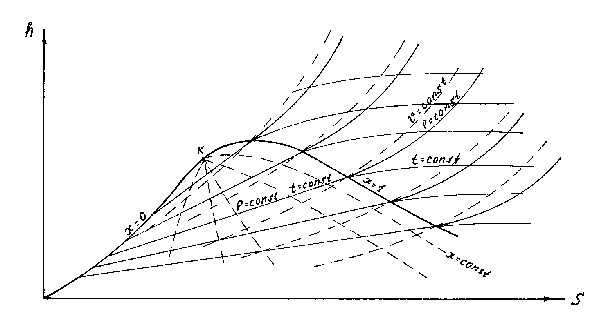
Рис. 8.5
Между пограничными кривыми будет влажный пар, над верхней пограничной кривой перегретый пар, слева от нижней пограничной кривой жидкость. Нижняя пограничная кривая будет соответствовать насыщенной жидкости, а верхняя пограничная кривая сухому пару при различных давлениях.
В области влажного пара изобары и изотермы совпадают (являясь линиями парообразования или кипения) и представляют собой слабо расходящиеся прямые линии. После верхней пограничной кривой изобары и изотермы расходятся. Изобары в виде логарифмических кривых поднимаются вверх, а изотермы направлены вправо. В области влажного пара наносятся линии постоянной степени сухости x = const. На диаграмме наносятся также изохоры u = const, которые идут под небольшим углом к изобарам. Обычно всю h, s-диаграмму не выполняют, а
вычеркивают только верхнюю часть, достаточную для нахождения встречающихся на практике параметров пара, и выполняют ее в большом масштабе.
27. Влажный воздух.
В сушильной технике в качестве рабочего тела широко используют влажный воздух, представляющий собой смесь сухого воздуха и водяного пара.
Содержание водяного пара в атмосферном воздухе зависит от метеорологических условий, а также от наличия источников испарения воды и колеблется в широких пределах: от малых долей до 4 % (по массе).
Смесь сухого воздуха и насыщенного водяного пара называется насыщенным влажным воздухом. Смесь сухого воздуха и перегретого водяного пара называется ненасыщенным влажным воздухом. Температура, до которой необходимо охлаждать ненасыщенный влажный воздух, чтобы содержащийся в нем перегретый пар стал насыщенным, называется температурой точки росы. При дальнейшем охлаждении влажного воздуха (ниже температуры точки росы) происходит конденсация водяного пара. Поэтому температуру точки росы часто используют как меру содержания в воздухе воды в парообразном состоянии.
Обычно к влажному воздуху применяют уравнения для идеальных газовых смесей. Так как в процессах сушки количество водяного пара в воздухе может меняться, а количество сухого воздуха остается постоянным, то целесообразно относить все величины к 1 кг сухого воздуха (а не смеси).
Влагосодержание, абсолютная и относительная влажность. Масса пара в 1 м3 влажного воздуха, численно равная плотности пара ρп при парциальном давлении рп, называется абсолютной влажностью. Отношение действительной абсолютной влажности воздуха ρn к максимально возможной абсолютной влажности ρs при той же температуре называют относительной влажностью и обозначают через φ: φ = ρn / ρs = рn /рs, где рп — парциальное давление водяного пара во влажном воздухе; р5 — максимально возможное парциальное давление водяного пара при данной температуре.
Величина ф выражается в процентах или относительных единицах. Поскольку 0 < рn < р5, то 0 < φ < 100%. Для сухого воздуха φ = 0, для насыщенного ф= 100 %.
Отношение массы водяного пара Мпсодержащегося во влажном воздухе, к массе сухого воздуха Мв
, называется влагосодержанием воздуха и измеряется в килограммах на килограмм: d = Мп / Мв.
Максимально возможное влагосодержание достигается при полном насыщении воздуха водяными парами (ф=1)
dиакс =0,622 (рs / p – рs) Если давление насыщенного пара становится равным внешнему давлению , что достигается при температуре кипения, то d= ∞.
Теплоемкость и энтальпия влажного воздуха. Изобарную теплоемкость влажного воздуха Ср обычно относят к 1 кг сухого воздуха, т. е. к (1 + d) кг влажного воздуха. Она равна сумме теплоемкостей 1 кг сухого воздуха и dкг пара: ср = срв + dсрп. В приближенных термодинамических расчетах процессов с влажным воздухом в небольшом диапазоне температур можно применять удельную изобарную теплоемкость сухого воздуха срв= 1 кДж/(кг-К) = const, удельную изобарную теплоемкость водяного пара срв=2 кДж/(кг- К) = const. В этом случае, выражая теплоемкость в кДж/( кг-К), получаем ср=1+2d.
Энтальпия влажного воздуха определяется как энтальпия газовой смеси, состоящей из 1 кг сухого воздуха и dкг водяного пара, т. е. h = hВ + dhп. Энтальпия 1 кг сухого воздуха, кДж/кг hв = срв t
28. Термодинамика потока газа или пара.
Под открытыми понимаются термодинамические системы, которые кроме обмена теплотой и работой с окружающей средой допускают также и обмен массой. В технике широко используются процессы преобразования энергии в потоке, когда рабочее тело перемещается из области с одними параметрами в область с другими. Это, например, расширение пара в турбинах, сжатие газов в компрессорах.
Будем рассматривать лишь одномерные стационарные потоки, в которых параметры зависят только от одной координаты, совпадающей с направлением вектора скорости, и не зависят от времени. Условие неразрывности течения в таких потоках заключается в одинаковости массового расхода m рабочего тела в любом сечении:
,
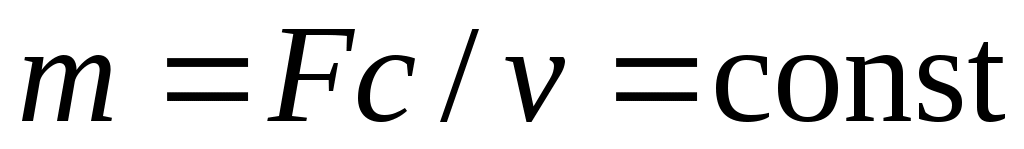где F— площадь поперечного сечения канала; с — скорость рабочего тела.
Рассмотрим термодинамическую
систему, представленную схематически на рисунке 7.1.
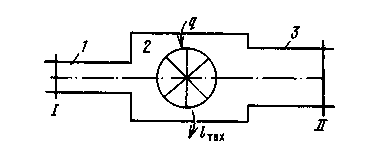
Рисунок 7.1 - Открытая термодинамическая система
По трубопроводу 1 рабочее тело с параметрами Т1 , p1, v1 подается со скоростью c1в тепломеханический агрегат 2 (двигатель, паровой котел, компрессор и т. д.). Здесь каждый килограмм рабочего тела в общем случае может получать от внешнего источника теплоту qи совершать техническую работу lтех, например, приводя в движение ротор турбины, а затем удаляется через выхлопной патрубок со скоростью с2, имея параметры Т2 , p2, v2.
Если в потоке мысленно выделить замкнутый объем рабочего тела и наблюдать за изменением его параметров в процессе перемещения, то для описания его поведения будут пригодны все полученные выше термодинамические соотношения и, в частности, первый закон термодинамики в обычной записи: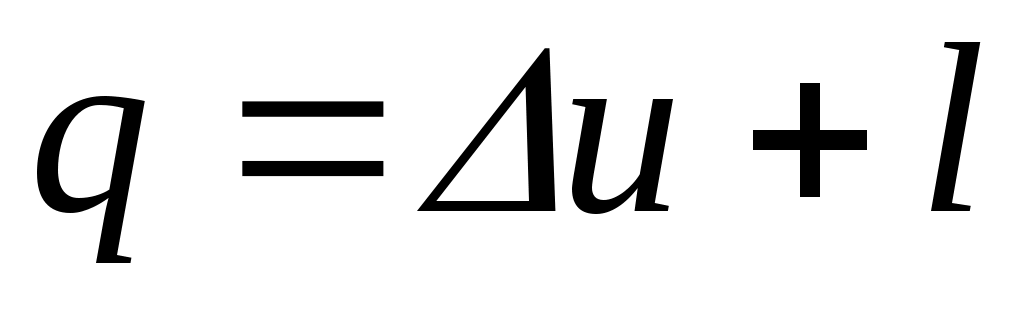
.
Внутренняя энергия есть функция состояния рабочего тела, поэтому значение определяется параметрами рабочего тела при входе (сечение потока I), а значение — параметрами рабочего тела при выходе из агрегата (сечение II).
Работа расширения l совершается рабочим телом на поверхностях, ограничивающих выделенный движущийся объем, т. е. на стенках агрегата и границах, выделяющих этот объем в потоке. Часть стенок агрегата неподвижна, и работа расширения на них равна нулю. Другая часть стенок специально делается подвижной (рабочие лопатки в турбине и компрессоре, поршень в поршневой машине), и рабочее тело совершает на них техническую работу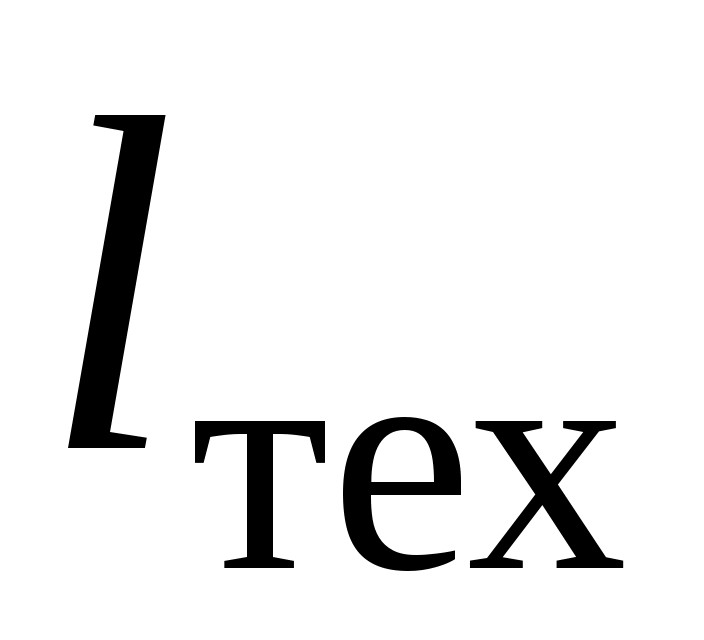
При входе рабочее тело вталкивается в агрегат. Для этого нужно преодолеть давление p1. Посколькуp1=const, то каждый килограмм рабочего тела может занять объем лишь при затрате работы, равной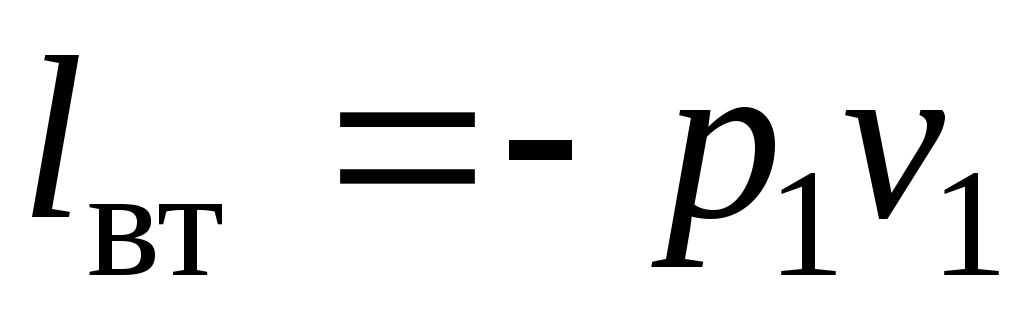
.
Для того чтобы выйти в трубопровод 3, рабочее тело должно вытолкнуть из него такое же количество рабочего тела, ранее находившегося в нем, преодолев
давление р2, т. е. каждый килограмм, занимая объем v2 должен произвести определенную работу выталкивания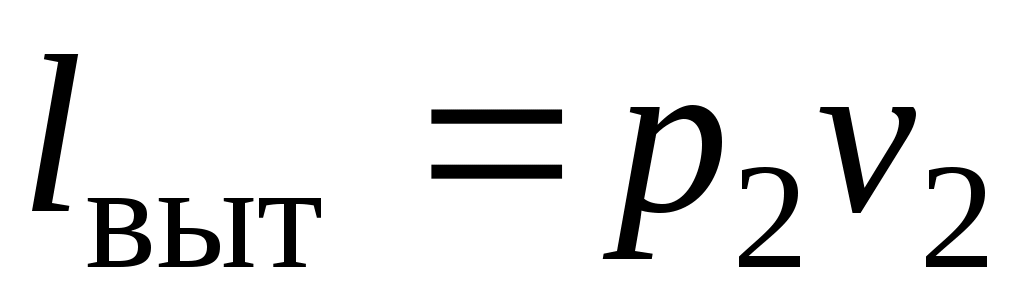
.
Сумма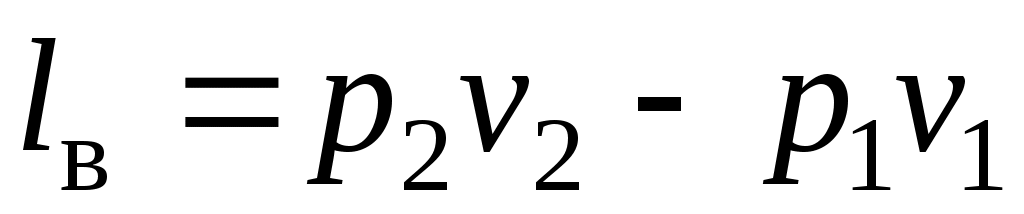
называется работой вытеснения.
Если скорость на выходе больше, чем на входе, то часть работы расширения будет затрачена на увеличение кинетической энергии рабочего тела в потоке, равное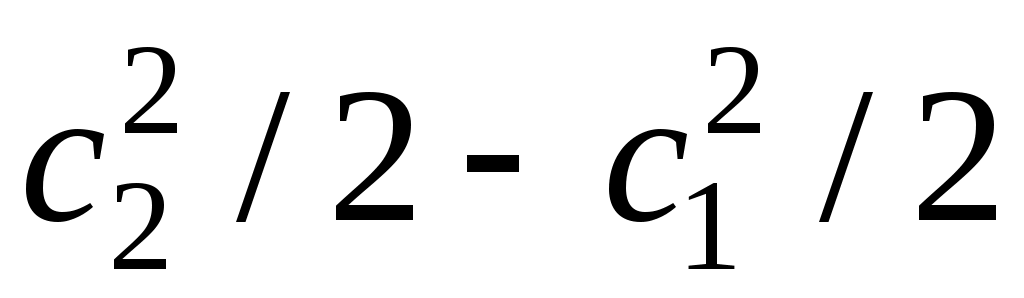
.
Наконец, в неравновесном процессе некоторая работа может быть затрачена на преодоление сил трения. Окончательно
.
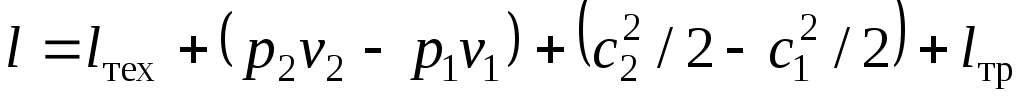Теплота, сообщенная каждому килограмму рабочего тела во время прохождения его через агрегат, складывается из теплоты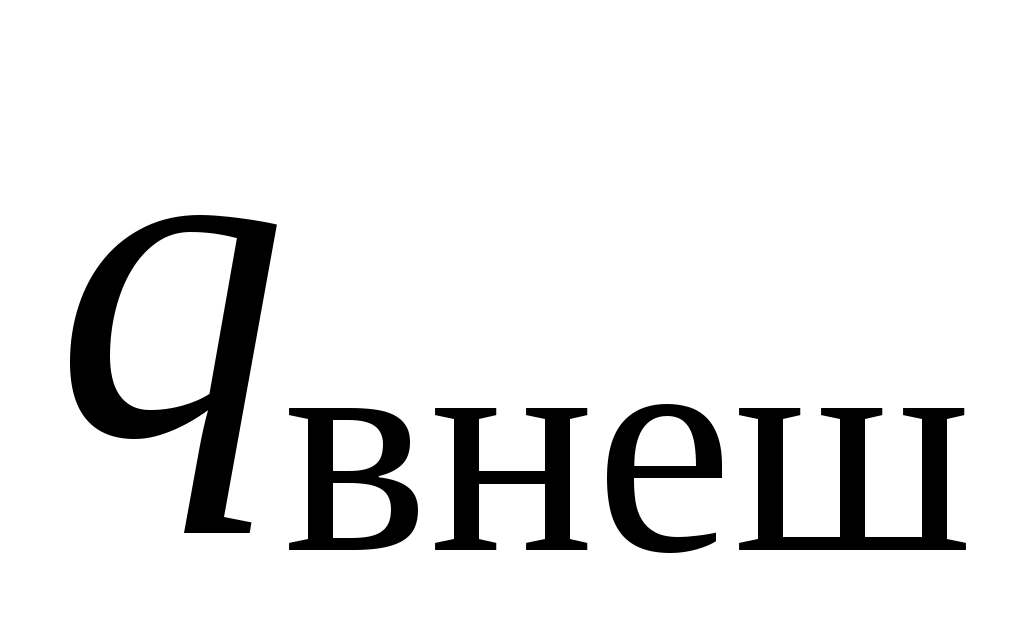
, подведенной снаружи, и теплоты 
, в которую переходит работа трения внутри агрегата, т. е. 
.
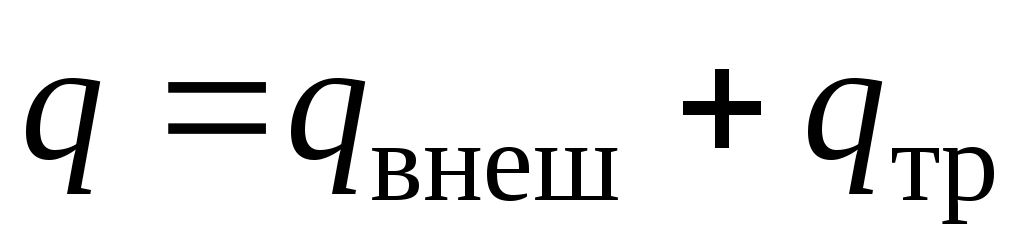Подставив полученные значения q и l в уравнение первого закона термодинамики, получим
.
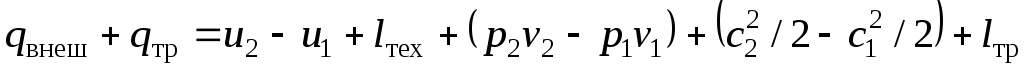Поскольку теплота трения равна работе трения, окончательно запишем:
.
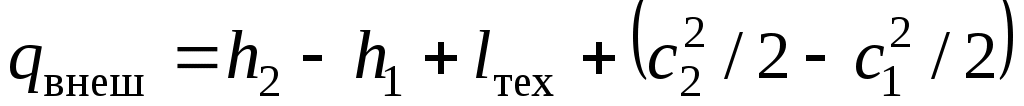Это и есть выражение первого закона термодинамики для потока, который можно сформулировать так: теплота, подведенная к потоку рабочего тела извне, расходуется на увеличение энтальпии рабочего тела, производство технической работы и увеличение кинетической энергии потока.
В дифференциальной форме уравнение записывается в виде
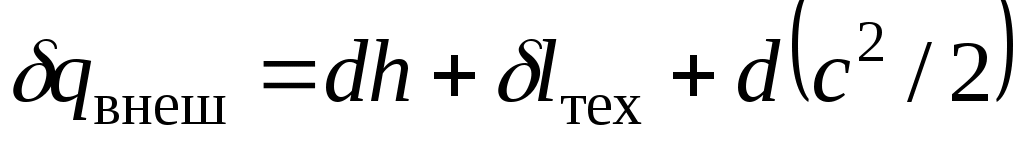. (7.1)
Оно справедливо как для равновесных
Соединяя точки с, с1, с2 ... и т.д., получим линию сухого насыщенного пара или верхнюю пограничную кривую. Точка соединения верхней и нижней пограничных кривых дает критическую точку к. Между пограничными кривыми лежит область влажного насыщенного пара. Правее и выше верхней пограничной кривой кс будет перегретый пар, а часть диаграммы, лежащая левее нижней пограничной кривой, ак будет областью жидкости. В области влажного пара наносят линии постоянной степени сухости x = const. На диаграмму также наносятся изохоры u = const.
Некоторым неудобством данной диаграммы является то, что при определении количества теплоты приходится измерять соответствующие площади.
Диаграмма h. s для водяного пара. Более удобной для расчетных целей является диаграмма h, s (диаграмма Молье). Одним из ее основных преимуществ перед T, s - диаграммой является то, что количество теплоты, участвующее в процессе, изображается линейным отрезком, а не площадью, как в системе координат T, s.
По значениям h¢, s¢, h², s², взятым из таблиц для разных давлений, строят верхнюю КВ и нижнюю ОК пограничные кривые (рис. 8.5).
Рис. 8.5
Между пограничными кривыми будет влажный пар, над верхней пограничной кривой перегретый пар, слева от нижней пограничной кривой жидкость. Нижняя пограничная кривая будет соответствовать насыщенной жидкости, а верхняя пограничная кривая сухому пару при различных давлениях.
В области влажного пара изобары и изотермы совпадают (являясь линиями парообразования или кипения) и представляют собой слабо расходящиеся прямые линии. После верхней пограничной кривой изобары и изотермы расходятся. Изобары в виде логарифмических кривых поднимаются вверх, а изотермы направлены вправо. В области влажного пара наносятся линии постоянной степени сухости x = const. На диаграмме наносятся также изохоры u = const, которые идут под небольшим углом к изобарам. Обычно всю h, s-диаграмму не выполняют, а
вычеркивают только верхнюю часть, достаточную для нахождения встречающихся на практике параметров пара, и выполняют ее в большом масштабе.
27. Влажный воздух.
В сушильной технике в качестве рабочего тела широко используют влажный воздух, представляющий собой смесь сухого воздуха и водяного пара.
Содержание водяного пара в атмосферном воздухе зависит от метеорологических условий, а также от наличия источников испарения воды и колеблется в широких пределах: от малых долей до 4 % (по массе).
Смесь сухого воздуха и насыщенного водяного пара называется насыщенным влажным воздухом. Смесь сухого воздуха и перегретого водяного пара называется ненасыщенным влажным воздухом. Температура, до которой необходимо охлаждать ненасыщенный влажный воздух, чтобы содержащийся в нем перегретый пар стал насыщенным, называется температурой точки росы. При дальнейшем охлаждении влажного воздуха (ниже температуры точки росы) происходит конденсация водяного пара. Поэтому температуру точки росы часто используют как меру содержания в воздухе воды в парообразном состоянии.
Обычно к влажному воздуху применяют уравнения для идеальных газовых смесей. Так как в процессах сушки количество водяного пара в воздухе может меняться, а количество сухого воздуха остается постоянным, то целесообразно относить все величины к 1 кг сухого воздуха (а не смеси).
Влагосодержание, абсолютная и относительная влажность. Масса пара в 1 м3 влажного воздуха, численно равная плотности пара ρп при парциальном давлении рп, называется абсолютной влажностью. Отношение действительной абсолютной влажности воздуха ρn к максимально возможной абсолютной влажности ρs при той же температуре называют относительной влажностью и обозначают через φ: φ = ρn / ρs = рn /рs, где рп — парциальное давление водяного пара во влажном воздухе; р5 — максимально возможное парциальное давление водяного пара при данной температуре.
Величина ф выражается в процентах или относительных единицах. Поскольку 0 < рn < р5, то 0 < φ < 100%. Для сухого воздуха φ = 0, для насыщенного ф= 100 %.
Отношение массы водяного пара Мпсодержащегося во влажном воздухе, к массе сухого воздуха Мв
, называется влагосодержанием воздуха и измеряется в килограммах на килограмм: d = Мп / Мв.
Максимально возможное влагосодержание достигается при полном насыщении воздуха водяными парами (ф=1)
dиакс =0,622 (рs / p – рs) Если давление насыщенного пара становится равным внешнему давлению , что достигается при температуре кипения, то d= ∞.
Теплоемкость и энтальпия влажного воздуха. Изобарную теплоемкость влажного воздуха Ср обычно относят к 1 кг сухого воздуха, т. е. к (1 + d) кг влажного воздуха. Она равна сумме теплоемкостей 1 кг сухого воздуха и dкг пара: ср = срв + dсрп. В приближенных термодинамических расчетах процессов с влажным воздухом в небольшом диапазоне температур можно применять удельную изобарную теплоемкость сухого воздуха срв= 1 кДж/(кг-К) = const, удельную изобарную теплоемкость водяного пара срв=2 кДж/(кг- К) = const. В этом случае, выражая теплоемкость в кДж/( кг-К), получаем ср=1+2d.
Энтальпия влажного воздуха определяется как энтальпия газовой смеси, состоящей из 1 кг сухого воздуха и dкг водяного пара, т. е. h = hВ + dhп. Энтальпия 1 кг сухого воздуха, кДж/кг hв = срв t
28. Термодинамика потока газа или пара.
Под открытыми понимаются термодинамические системы, которые кроме обмена теплотой и работой с окружающей средой допускают также и обмен массой. В технике широко используются процессы преобразования энергии в потоке, когда рабочее тело перемещается из области с одними параметрами в область с другими. Это, например, расширение пара в турбинах, сжатие газов в компрессорах.
Будем рассматривать лишь одномерные стационарные потоки, в которых параметры зависят только от одной координаты, совпадающей с направлением вектора скорости, и не зависят от времени. Условие неразрывности течения в таких потоках заключается в одинаковости массового расхода m рабочего тела в любом сечении:
,где F— площадь поперечного сечения канала; с — скорость рабочего тела.
Рассмотрим термодинамическую
систему, представленную схематически на рисунке 7.1.
Рисунок 7.1 - Открытая термодинамическая система
По трубопроводу 1 рабочее тело с параметрами Т1 , p1, v1 подается со скоростью c1в тепломеханический агрегат 2 (двигатель, паровой котел, компрессор и т. д.). Здесь каждый килограмм рабочего тела в общем случае может получать от внешнего источника теплоту qи совершать техническую работу lтех, например, приводя в движение ротор турбины, а затем удаляется через выхлопной патрубок со скоростью с2, имея параметры Т2 , p2, v2.
Если в потоке мысленно выделить замкнутый объем рабочего тела и наблюдать за изменением его параметров в процессе перемещения, то для описания его поведения будут пригодны все полученные выше термодинамические соотношения и, в частности, первый закон термодинамики в обычной записи:
.Внутренняя энергия есть функция состояния рабочего тела, поэтому значение определяется параметрами рабочего тела при входе (сечение потока I), а значение — параметрами рабочего тела при выходе из агрегата (сечение II).
Работа расширения l совершается рабочим телом на поверхностях, ограничивающих выделенный движущийся объем, т. е. на стенках агрегата и границах, выделяющих этот объем в потоке. Часть стенок агрегата неподвижна, и работа расширения на них равна нулю. Другая часть стенок специально делается подвижной (рабочие лопатки в турбине и компрессоре, поршень в поршневой машине), и рабочее тело совершает на них техническую работу
При входе рабочее тело вталкивается в агрегат. Для этого нужно преодолеть давление p1. Посколькуp1=const, то каждый килограмм рабочего тела может занять объем лишь при затрате работы, равной
.Для того чтобы выйти в трубопровод 3, рабочее тело должно вытолкнуть из него такое же количество рабочего тела, ранее находившегося в нем, преодолев
давление р2, т. е. каждый килограмм, занимая объем v2 должен произвести определенную работу выталкивания
.Сумма
называется работой вытеснения.Если скорость на выходе больше, чем на входе, то часть работы расширения будет затрачена на увеличение кинетической энергии рабочего тела в потоке, равное
.Наконец, в неравновесном процессе некоторая работа может быть затрачена на преодоление сил трения. Окончательно
.Теплота, сообщенная каждому килограмму рабочего тела во время прохождения его через агрегат, складывается из теплоты
, подведенной снаружи, и теплоты , в которую переходит работа трения внутри агрегата, т. е. .Подставив полученные значения q и l в уравнение первого закона термодинамики, получим
.Поскольку теплота трения равна работе трения, окончательно запишем:
.Это и есть выражение первого закона термодинамики для потока, который можно сформулировать так: теплота, подведенная к потоку рабочего тела извне, расходуется на увеличение энтальпии рабочего тела, производство технической работы и увеличение кинетической энергии потока.
В дифференциальной форме уравнение записывается в виде
. (7.1)Оно справедливо как для равновесных