Файл: Элементы специальной теории относительности.docx

ХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХ

ХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХХ

ХХХХХХХХХХХХХХХХХХ


РЕФЕРАТ

По дисциплине «________________________»

Тема «Элементы специальной теории относительности»

Выполнила студент гр. _____________

___________________________________

Проверил: __________________________


________________ 2022

Оглавление

Введение

Специальная теория относительности была разработана в конце XIX – начале XX века усилиями Г. А. Лоренца, А. Пуанкаре, Лармора и А. Эйнштейна, и затем представлена Минковским в четырёхмерном формализме, объединяющем пространство и время. Вопрос приоритета в создании СТО имеет дискуссионный характер: основные положения и полный математический аппарат теории, включая групповые свойства преобразований Лоренца, в абстрактной форме были впервые сформулированы А. Пуанкаре в работе 1905 г. «О динамике электрона» на основе предшествующих результатов Г. А. Лоренца, а явный абстрактный вывод базиса теории — преобразований Лоренца, из минимума исходных постулатов был дан А. Эйнштейном в практически одновременной работе 1905 г. «К электродинамике движущихся сред». Однако Лармор ещё в 1897 г., до работы Лоренца 1899 г., приходит к преобразованиям Лоренца. Он также даёт релятивистскую формулу сложения скоростей.

Имя Эйнштейна неразрывно связано с великой революцией в физике, свершившейся в начале века, – с созданием квантовой теории и теории относительности, причем вклад Эйнштейна в становление современной физической картины мира оказался определяющим. Он стоял у колыбели квантовой механики. Ему принадлежат первоклассные работы по статистике. Именно за работы в этих областях в 1921 г. ему была присуждена Нобелевская премия. Эйнштейну мы воздаем славу как человеку, сказавшему решительное слово в формировании специальной теории относительности, взявшему ответственность за ее физическое содержание и последовательно отстаивавшему созданную теорию, а также как создателю общей теории относительности. Теория относительности Эйнштейна перестала быть академическим учением – сейчас ею интересуются очень широкие круги. Ведь без эйнштейновской формулы о взаимосвязи энергии и массы нельзя понять ядерные процессы, а замедленное старение организмов в условиях быстрого движения волнует умы многих в связи с проблемами полета к далеким звездам. Велико и мировоззренческое значение теории относительности, так как она затрагивает коренные свойства времени и пространства[1].

---

Целью данной работы является изучение элементов СТО, выполнив следующие задачи: рассмотреть принцип теории относительности Эйнштейна, преобразование координат и скоростей по Лоренцу, длительности событий в разных системах отсчёта и релятивистскую энергию и импульс.

1. Принцип теории относительности Эйнштейна

1.1 Создание СТО

Предпосылкой к созданию теории относительности явилось развитие в XIX веке электродинамики. Результатом обобщения и теоретического осмысления экспериментальных фактов и закономерностей в областях электричества и магнетизма стали уравнения Максвелла, описывающие все проявления электромагнитного поля и его взаимодействие с зарядами и токами.

Другим следствием развития электродинамики стал переход от ньютоновской концепции дальнодействия (согласно которой взаимодействующие на расстоянии тела воздействуют друг на друга через разделяющую их пустоту, причём взаимодействие осуществляется с бесконечной скоростью, т.е. «мгновенно») к концепции близкодействия, предложенной Майклом Фарадеем. В ней взаимодействие передаётся с помощью промежуточных агентов – полей, заполняющих пространство – и при этом встал вопрос о скоростях распространения как взаимодействий, переносимых полями, так и самих полей. Скорость распространения электромагнитного поля в пустоте вытекала из уравнений Максвелла и оказалась постоянной и равной скорости света.

В связи с этим появляется новый вопрос – относительно чего постоянна скорость света? В максвелловой электродинамике скорость распространения электромагнитных волн (при условии измерения этой скорости с помощью электромагнитных часов и положения часов с помощью света) оказалась не зависящей от скоростей движения как источника этих волн, так и наблюдателя. Аналогичной оказалась и ситуация с магнитостатическими решениями, вытекающими из уравнений Максвелла: статические магнитные поля и силы Лоренца, действующие на движущиеся в магнитных полях заряды, зависят от скоростей зарядов по отношению к наблюдателю, т.е. уравнения Максвелла оказались неинвариантными относительно принципа относительности и преобразований Галилея. А это противоречило ньютоновской концепции абсолютного пространства классической механики.

1.2. Постулаты СТО

СТО полностью выводится на физическом уровне строгости из пяти постулатов (предположений):

---

1. Справедлив принцип относительности Пуанкаре-Эйнштейна, являющийся расширением принципа относительности Галилея на все явления.

2. Скорость света не зависит от скорости движения как источников, так и приёмников во всех инерциальных системах отсчёта. Это позволяет дистанционно произвести однозначную первоначальную синхронизацию всех имеющихся часов как в неподвижной, так и в движущейся системе отсчёта.

3. Справедливость симметрий относительно поворотов в пространстве-времени Евклида.

4. Справедливость симметрий относительно сдвигов в пространстве-времени Евклида.

5. Пространственно-временные измерения осуществляются с помощью электромагнитных волн.

Формулировка второго постулата может быть шире: «Скорость света постоянна во всех инерциальных системах отсчёта», но для вывода СТО достаточно его формулировки, записанной выше. Некоторые постулаты сформулированы явно, а другие предполагаются неявным образом как в работах Эйнштейна, так и Пуанкаре, хотя и в разной степени.

Иногда пятый постулат СТО записывают как синхронизацию часов по А. Эйнштейну, но принципиального значения это не имеет: при различных условиях синхронизации изменяется математическое описание экспериментальной ситуации без изменения предсказываемых и измеряемых эффектов. Пятый постулат СТО является ключевым, так как без него скорость света не смогла бы появиться в преобразованиях Лоренца для координат и времени и в других формулах[2].

Раньше можно было встретить утверждение о том, что СТО обосновывает существование скорости света как предельной скорости распространения сигналов. Естественно, что это не может быть доказано в рамках СТО, которая не является теорией о распространении сигналов, а лишь использует свет в процессе измерений.

2. Преобразование координат и скоростей (по Лоренцу)

Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x', y', z') и моментом времени t' этого же события, наблюдаемого в системе отсчета K'.

Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

---

K' → K K → K'





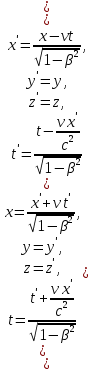
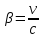
Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x' системы K' происходит процесс длительностью τ₀ = t'₂ – t'₁ (собственное время), где t'₁ и t'₂ – показания часов в системе K' в начале и конце процесса. Длительность τ этого процесса в системе K будет равна



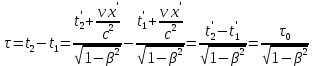
Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K' (x'₁ ≠ x'₂) одновременно с точки зрения наблюдателя в K' (t'₁ = t'₂ = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь






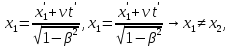
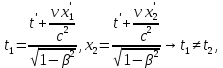
Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t₂ – t₁ определяется знаком выражения υ(x'₂ – x'₁), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.

Относительность одновременности пространственно-разобщенных событий можно проиллюстрировать на следующем примере.

Пусть в системе отсчета K' вдоль оси x' неподвижно расположен длинный жесткий стержень. В центре стержня находится импульсная лампа B, а на его концах установлены двое синхронизованных часов (рис.1(a)), система K' движется вдоль оси x системы K со скоростью υ. В некоторый момент времени лампа посылает короткие световые импульсы в направлении концов стержня. В силу равноправия обоих направлений свет в системе K' дойдет до концов стержня одновременно, и часы,

---

закрепленные на концах стержня, покажут одно и то же время t'. Относительно системы K концы стержня движутся со скоростью υ так, что один конец движется навстречу световому импульсу, а другой конец свету приходится догонять. Так как скорости распространения световых импульсов в обоих направлениях одинаковы и равны c, то, с точки зрения наблюдателя в системе K, свет раньше дойдет до левого конца стержня, чем до правого (рис. 1(b)).



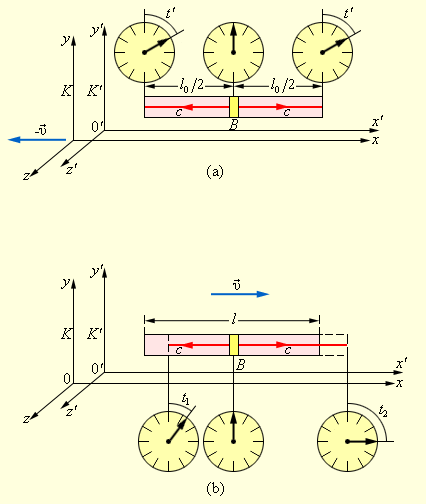
Рисунок 1. Относительность одновременности. Световой импульс достигает концов твердого стержня одновременно в системе отсчета K' (a) и не одновременно в системе отсчета K (b)
Преобразования Лоренца выражают относительный характер промежутков времени и расстояний. Однако, в СТО наряду с утверждением относительного характера пространства и времени важную роль играет установление инвариантных физических величин, которые не изменяются при переходе от одной системы отсчета к другой. Одной из таких величин является скорость света в вакууме c, которая в СТО приобретает абсолютный характер. Другой важной инвариантной величиной, отражающей абсолютный характер пространственно-временных связей, является интервал между событиями[3].

Пространственно-временной интервал определяется в СТО следующим соотношением:



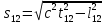
где t₁₂ – промежуток времени между событиями в некоторой системе отсчета, а l₁₂ – расстояние между точками, в которых происходят рассматриваемые события, в той же системе отсчета. В частном случае, когда одно из событий происходит в начале координат (x₁ = y₁ = z₁ = 0) системы отсчета в момент времени t₁ = 0, а второе – в точке с координатами x, y, z в момент времени t, пространственно-временной интервал между этими событиями записывается в виде



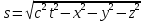
С помощью преобразований Лоренца можно доказать, что пространственно-временной интервал между двумя событиями не изменяется при переходе из одной инерциальной системы в другую. Инвариантность интервала означает, что, несмотря на относительность расстояний и промежутков времени, протекание физических процессов носит объективный характер и не зависит от системы отсчета.

---