Файл: Элементы специальной теории относительности.docx

Если одно из событий представляет собой вспышку света в начале координат системы отсчета при t = 0, а второе – приход светового фронта в точку с координатами x, y, z в момент времени t, то

x² + y² + z² = c²t²

и, следовательно, интервал для этой пары событий s = 0. В другой системе отсчета координаты и время второго события будут другими, но и в этой системе пространственно-временной интервал s' окажется равным нулю, так как

x'² + y'² + z'² = c²t'²,

Для любых двух событий, связанных между собой световым сигналом, интервал равен нулю.

Из преобразований Лоренца для координат и времени можно получить релятивистский закон сложения скоростей. Пусть, например, в системе отсчета K' вдоль оси x' движется частица со скоростью:



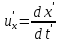
Составляющие скорости частицы u'_x и u'_z равны нулю. Скорость этой частицы в системе K будет равна:



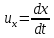
С помощью операции дифференцирования из формул преобразований Лоренца можно найти:



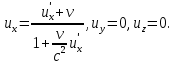
Эти соотношения выражают релятивистский закон сложения скоростей для случая, когда частица движется параллельно относительной скорости 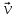систем отсчета K и K'.

При 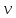<< c релятивистские формулы переходят в формулы классической механики: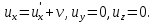



Если в системе K' вдоль оси x' со скоростью u'_x = c распространяется световой импульс, то для скорости u_x импульса в системе K получим



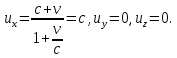
Таким образом, в системе отсчета K световой импульс также распространяется вдоль оси x со скоростью c, что согласуется с постулатом об инвариантности скорости света.

3. Длительность событий в разных системах отсчёта

Пусть в точке х', неподвижной относительно системы K', происходит событие длящееся время


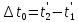
Началу события соответствует в этой системе координата

---

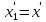и момент времени 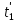, концу события - координата 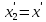и момент времени 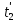. Относительно системы K точка, в которой происходит событие, перемещается. Согласно преобразованиям Лоренца, началу и концу события соответствуют в системе K'.

;

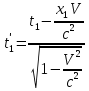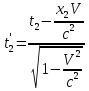
Откуда:

;

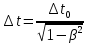Или:

/

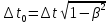Время 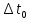, отсчитанное по часам, движущимся вместе с телом, называют собственным временем этого тела. Как видно из уравнения, собственное время всегда меньше, чем время, отсчитанное по часам, движущимся относительно тела. Релятивистский эффект замедления хода времени позволяет в принципе осуществить «путешествие в будущее» (но не в прошлое). В самом деле, пусть космический корабль, движущийся со скоростью 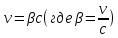относительно Земли, совершает перелет от Земли до некоторой звезды и обратно. Если свет проходит путь l₀ от звезды до Земли за время t₀, то l₀ = ct₀ и для земного наблюдателя продолжительность перелета равна: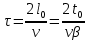



Именно настолько постареют люди на Земле к моменту возвращения космонавтов. С другой стороны, по часам, установленным на космическом корабле, полет займет меньшее время 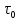, которое: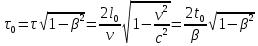



В соответствии с принципом относительности все процессы на космическом корабле (в том числе и процесс старения космонавтов) идут так же, как и на Земле, но не по земным часам, а по часам, установленным на корабле. Пусть, например, t₀= 500 лет и β = 0,9999. Тогда

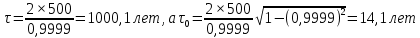
4. Релятивистская энергия и импульс

4.1 Импульс. Релятивистская масса

Принцип относительности Эйнштейна утверждает инвариантность всех законов природы по отношению к переходу от одной инерциальной системе отсчета к другой. Отсюда следует, что уравнения, которые описывают законы природы, должны быть инвариантны относительно преобразований Лоренца.

---

Во время создания СТО теории, удовлетворяющей данному условию, она подразумевала уже существующую теорию электродинамики Максвелла. Уравнения вышли неинвариантными относительно преобразований Лоренца, что требовало пересмотра и уточнения законов механики.

Для этого Эйнштейн основывался на требованиях выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Чтобы он выполнялся во всех инерционных системах отсчета, следовало изменить определение импульса тела.

Классический импульс 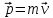заменяют релятивистским 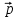с массой m и скоростью движения 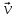. Запись принимает вид: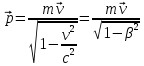



Если данное определение задействовать при решении, то закон сохранения суммарного импульса частиц выполнится во всех инерциальных системах, в которых есть связь с преобразованиями Лоренца. Когда β→0 релятивистский импульс перейдет в классический.

Масса m считается фундаментальной характеристикой частицы. Она не зависит от выбора инерциальной системы отсчета, скорости движения.

Некоторые учебники трактуют это как массу покоя, обозначаемую m₀. Позже вводилась релятивистская масса частицы 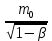, которая зависела от скорости движения частицы. Современная физика отказывается от данных терминологий[4].

Запись основного закона релятивистской динамики материальной точки принимает вид, аналогичный второму закону Ньютона:



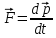
тогда 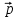примет значение релятивистского импульса частицы. Отсюда следует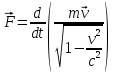


Скорость частицы в релятивистской механике не пропорциональна релятивистскому импульсу, то есть скорость изменения не будет пропорциональна ускорению. Отсюда имеем, что сила постоянна по модулю и по направлению, причем не вызывает равноускоренного движения. Если существует одномерное движение вдоль Ох, тогда ускорение частицы

---

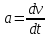с постоянной F равняется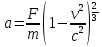

4.2 Движение релятивистской частицы

При росте скорости классической частицы под действием постоянной силы, скорость релятивистской частицы не превышает скорость света сс в пустоте.

Это очевидно, так как выполняется закон сохранения энергии релятивистской частицы. Определение E_k производится через работу внешней силы, которая необходима для сообщения телу заданной скорости. При разгоне частицы с массой m из состояния покоя до скорости ν₀ действует постоянная сила, совершающая работу



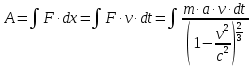
Так как α dt=dν, то запись примет вид



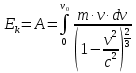
При вычислении интеграла произойдет упрощение выражения:



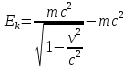
Интерпретация Эйнштейном первого члена правой части звучит как полная энергия Е движущейся частицы, а второго – энергией покоя E₀:

,

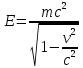E₀=mc².

Кинетической энергией E_k считают разность между полной Е и энергией покоя E₀. Запись принимает вид:

E_k=E−E₀.

На рисунке 2 изображено изменение E_k частицы, подчиняющейся классическому и релятивистскому законам.



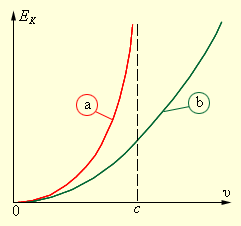
Рисунок 2. Зависимость кинетической энергии от скорости для релятивистской (a) и классической (b) частиц. При υ оба закона совпадают.
Вывод релятивистской механики в том, что масса m, находящаяся в покое, содержит большое количество энергии. Это применяется при ядерной энергии. Если наблюдалось уменьшение массы частицы на Δm, тогда выделившаяся энергия примет вид ΔE=Δm⋅c². Проводимые эксперименты дают понять, что существование энергии покоя реальное. Первый, кто подтвердил это, был Эйнштейн. Он использовал отношение, связывающее массу и энергию, полученное при их сравнении. При бета-распаде свободного нейтрона появлялись протон, электрон и антинейтрино с нулевой массой:

n→p+e⁻+

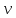
Конечные продукты обладали суммарной кинетической энергией, равной 1,25⋅10⁻¹³ Дж.

Масса нейтрона значительно превышает суммарную массу протона и электрона на Δm=13,9⋅10⁻³¹ кг. Так как прослеживается уменьшение массы, необходимо использовать соответствующую энергию ΔE=Δm⋅c²=1,25⋅10⁻¹³ Дж. Она равняется кинетической энергии релятивистской частицы.

4.3 Связь между энергией и импульсом релятивистской частицы

Самым важным выводом СТО является закон пропорциональности массы и энергии. Они обладают различными свойствами материи. Масса тела говорит о его инертности или способности вступать в гравитационное взаимодействие с другими телами. Важное свойство энергии – это способность превращения из одной формы в другую во время различных физических процессов, что подтверждает закон сохранения энергии.

Масса и энергия пропорциональны и выражают внутреннюю сущность материи.

Получаем, что формула Эйнштейна E₀=mc² выражает фундаментальный закон природы, называемый законом взаимосвязи массы и энергии.

Если скомбинировать выражения

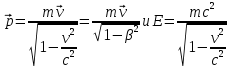, то придем к связывающему их соотношению.

Для этого следует переписать эти формулы в упрощенном виде





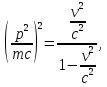
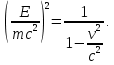
После почленного вычитания получаем



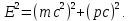
Следовательно, что для покоящихся частиц энергия фиксируется как E=E₀=mc²

Исходя из соотношения становится понятно, что частица может обладать энергией и импульсом, но не иметь массы, то есть m=0. Она получила название безмассовой. Для нее используется формула связи энергии и импульса в виде E=pc.

К частицам, которые не имеют массы, относят фотоны, называемые квантами электромагнитного излучения, и нейтрино. Существование безмассовых частиц в покое невозможно, поэтому их движение характеризуется предельной скоростью c[5].

Заключение

Теория относительности А. Эйнштейна – физическая теория, рассматривающая пространственно-временные свойства физических процессов. Так как закономерности, устанавливаемые теорией относительности, – общие для всех физических процессов, то обычно о них говорят просто как о свойствах пространства-времени. Эти свойства зависят от полей тяготения в данной области пространства-времени. Теория, описывающая свойства пространства-времени в приближении, когда полями тяготения можно пренебречь, называется специальной или частной теорией относительности, или просто теорией относительности. Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности, называемой также теорией тяготения Эйнштейна. Физические явления, описываемые теорией относительности, называются релятивистскими и проявляются при скоростях 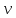движения тел, близких к скорости света в вакууме.

В основе теории относительности лежат два положения: принцип относительности, означающий равноправие всех инерциальных систем отсчета, и постоянство скорости света в вакууме, ее независимость от скорости движения источника света. Эти два постулата определяют формулы перехода от одной инерциальной системы отсчета к другой – преобразования Лоренца, для которых характерно, что при таких переходах изменяются не только пространственные координаты, но и моменты времени (относительность времени). Из преобразований Лоренца получаются основные эффекты специальной теории относительности: существование предельной скорости передачи любых взаимодействий – максимальной скорости, до которой можно ускорить тело, совпадающей со скоростью света в вакууме; относительность одновременности (события, одновременные в одной инерциальной системе отсчета, в общем случае не одновременны в другой); замедление течения времени в быстро движущемся теле и сокращение продольных – в направлении движения – размеров тел и др. Все эти закономерности теории относительности надежно подтверждены на опыте.

Теория относительности выявила ограниченность представлений классической физики об «абсолютных» пространстве и времени, неправомерность их обособления от движущейся материи; она дает более точное, по сравнению с классической механикой, отображение объективных процессов реальной действительности.

Ряд выводов общей теории относительности качественно отличаются от выводов ньютоновской теории тяготения. Важнейшие среди них связаны с возникновением черных дыр, сингулярностей пространства-времени, существованием гравитационных волн (гравитационного излучения).

Представления о пространстве и времени составляют основу физического миропонимания, что уже само по себе определяет значение теории относительности. Особенно велика ее роль в физике ядра и элементарных частиц, в том числе и для расчетов гигантских установок, которые предназначены для потоков очень быстрых частиц, необходимых для экспериментов, позволяющих продвинуться в изучении строения материи[6].

В данной работе мы рассмотрели принцип теории относительности Эйнштейна, преобразование координат и скоростей по Лоренцу, длительности событий в разных системах отсчёта и релятивистскую энергию и импульс.

Таким образом задачи выполнены, цель достигнута.

Список использованных источников

1. Шилов, В.Ф. Квантовая физика / В.Ф. Шилов. - М.: Просвещение, 2016. - 126 c.

2. Рашевский, П. К. Риманова геометрия и тензорный анализ. Часть 1. Евклидовы пространства и аффинные пространства. Тензорный анализ. Математические основы специальной теории относительности: моногр. / П.К. Рашевский. - М.: Красанд, 2019. - 352 c.

3. Франкфурт, У. И. Очерки по истории специальной теории относительности / У.И. Франкфурт. - Москва: ИЛ, 2017. - 200 c.

4. Угаров, В.А. Специальная теория относительности / В.А. Угаров. - Москва: Огни, 2010. - 922 c.

5. Фок, В. А. Квантовая физика и строение материи / В.А. Фок. - М.: Либроком, 2010. - 663 c.

6. Мицкевич, Н. В. Релятивистская физика. Специальная теория относительности. Общая теория относительности / Н.В. Мицкевич. - М.: Либроком, 2014. - 200 c.

---