Файл: Опорный конспект.doc

Цей шифр абсолютно надійний, якщо набір ключів дійсно випадковий і непередбачений. Якщо криптоаналітик спробує використати для заданого шифротексту всі можливі набори ключів і відновити всі можливі варіанти вихідного тексту, то вони всі матимуть однакову ймовірність. Не існує способу вибрати вихідний текст, що був дійсно посланий. Теоретично доведено, що одноразові системи не можуть бути розкриті без ключа, оскільки шифротекст не містить достатньої інформації для відновлення відкритого тексту.

На перший погляд здається, що завдяки абсолютній стійкості одноразової системи варто було б застосовувати її у всіх випадках, що вимагають абсолютної інформаційної безпеки. Однак можливості застосування одноразової системи обмежені лише практичними аспектами. Істотним моментом є вимога одноразового використання випадкової ключової послідовності. Ключова послідовність із довжиною, не меншої довжини повідомлення, повинна передаватися одержувачу повідомлення заздалегідь або окремо по деякому секретному каналу зв’язку. Ця вимога не буде занадто обтяжною для передавання дійсно важливих одноразових повідомлень. Однак така вимога практично нездійсненна для сучасних систем обробки інформації, де потрібно шифрувати багато мільйонів символів.

У деяких варіантах одноразового блокнота удаються до більш простого керування ключовою послідовністю, але це приводить до деякого зниження надійності шифру. Наприклад, ключ визначається вказівкою місця в книзі, відомої відправникові й одержувачеві повідомлення. Ключова послідовність починається із зазначеного місця цієї книги й використовується в такий самий спосіб, як у системі Віженера. Іноді такий шифр називають шифром із ключем, що біжить. Керування ключовою послідовністю в такому випадку набагато простіше, тому що довга ключова послідовність може бути представлена в компактній формі. Але з іншого боку, ці ключі не будуть випадковими. Тому у криптоаналітика з'являється можливість використати інформацію про частоти букв вихідної природної мови.

5 Шифрування методом Вернама

Значний внесок у розвиток криптографії зробив американець Г. Вернам. У 1917 році він, будучи співробітником телеграфної компанії, запропонував ідею автоматичного шифрування телеграфних повідомлень, суть якої полягає в наступному.

Відкритий текст представляється в коді Бодо (у вигляді п'ятизначних імпульсних комбінацій). У цьому коді, наприклад, буква «А» мала вигляд (+ + – – –). На паперовій стрічці ця буква одержувала такий вигляд (рис. 3) .

Знак «+» означав отвір, а знак «-» – його відсутність. При зчитуванні зі стрічки п'ятірка металевих щупів «пізнавала» отвір (при наявності отвору щуп замикав електричний ланцюг) і на лінії зв'язку посилався імпульс струму (рис. 4).

Рисунок 3 – Паперова стрічка системи Вернама

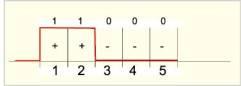
Рисунок 4 – Імпульс струму в системі Вернама

Вернам запропонував електромеханічно покоорди-натно додавати імпульси знаків секретного тексту з імпульсами гами.

Гама – це секретний ключ, що представляє хаотичний набір літер того самого алфавіту.

Додавання здійснювалося за модулем 2.

0  0 = 0,

0  1 = 1,

1  0 = 1,

1  1 = 0 ,

де

 – операція додавання за модулем 2,

0 – знак «-» коду Бодо,

1 – знак «+» коду Бодо.

Нехай, наприклад, знак гами має вигляд

+ – + – – (10100).

Тоді буква «А» при шифруванні переходить у двійкову комбінацію 01100 (– + + – –).

При розшифруванні необхідно повторити покоординатно ту саму операцію

(01100)  (10100) = (11000) = А.

Схема шифрування методом Вернама подана на рисунку 5

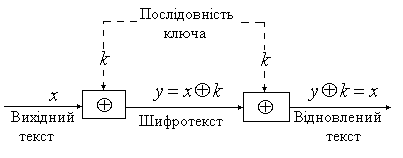
Рисунок 5 – Схема шифрування та розшифрування повідомлень методом Вернама

Вернам створив пристрій, що робить зазначені операції автоматично, без участі шифрувальника. Тим самим дав початок лінійному шифруванню, коли процеси шифрування та передачі повідомлення відбуваються одночасно. До цього шифрування було попереднім, тому лінійне шифрування істотно підвищувало оперативність зв'язку.

Відзначимо одну важливу особливість шифру Вернама, що послужила надалі обґрунтуванню теорії досконалого шифру, яку було запропоновано американським класиком криптографії К. Шенноном. Справа в тому, що при застосуванні шифру Вернама за перехопленим шифрованим текстом видгляу  може ховатися будь-який відкритий текст . Будь-якому відкритому тексту можна підібрати гаму, що породжує даний шифрований текст. Оскільки гама є ключем, то за перехопленням шифрованого повідомлення неможливо відкинути жодного відкритого тексту тієї самої довжини. Зусилля дешифровальників зводяться на “ні”.

Шифр Вернама має виняткову криптографічну стійкість. У той самий час стає ясним і недолік цієї системи шифрування. Хаотична гама (ключ) повинна мати ту саму довжину, що й відкритий текст. Для розшифрування на кінець лінії зв'язку, що приймає інформацію, необхідно передати (по таємних, захищених каналах) гаму достатньої довжини. При практичній реалізації це породжує істотні проблеми, причому досить істотні, що й визначило досить скромне поширення шифрів Вернама.

У цій ситуації був запропонований простий вихід: гама шифру записувалася на стрічку, склеєну в кільце. Таким чином, вона ставала не випадковою, а періодичною (як у шифрі Віженера). Шифр ставав нестійким.

Сам Вернам не був математиком-криптографом. Проте він наполягав на тому, що гама шифру не повинна повторюватися при шифруванні, і в цьому він був правий. Його ідеї покладені в основу нових підходів до надійного захисту інформації при передаванні значних за обсягом повідомлень.

6 Роторні машини

У 20-х роках XX століття були винайдені електромеханічні пристрої шифрування, що автоматизують процес шифрування. Принцип роботи таких машин заснований на багатоалфавітній заміні символів вихідного тексту згідно з значенням довгого ключа відповідно до версії шифру Віженера. Більшість із них – американська машина SIGABA (М-134), англійська TYPEX, німецька ENIGMA, японська PURPLE - були роторними машинами.

Головною деталлю роторної машини є ротор (або колесо) із дротовими перемичками усередині. Ротор має форму диска (розміром з хокейну шайбу). На кожній стороні диска рівномірно по колу розташовано m електричних контактів, де m – число знаків алфавіту (у випадку латинського алфавіту m=26). Кожен контакт на передній стороні диска з'єднаний з одним із контактів задньої сторони, як показано на рис. 6. У результаті електричний сигнал, що являє собою символ відкритого тексту, буде поданий відповідно до того, як він проходить через ротор від передньої сторони до задньої. Наприклад, ротор можна закомутувати дротовими перемичками для підстановки G замість A, U замість В, R замість С і т.д.

Ротори () можна об'єднати в банк роторів таким чином, щоб вихідні контакти одного ротора торкалися вхідних контактів наступного ротора (рис. 6). При цьому електричний імпульс від натиснутої клавіші з буквою вихідного тексту, що входить із одного кінця банку роторів, буде переставлятися кожним з роторів, доти, поки не залишить банк.

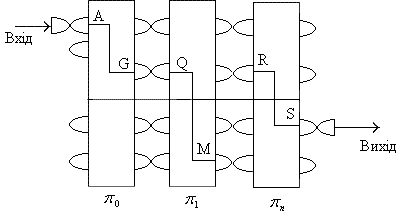
Рисунок 6 – Банк роторів

Шифротекст отриманий за допомогою роторної машини ускладнюється ще й тим, що ротори можуть обертатися по осі відносно один одного. Для одержання стійкої криптографічної системи розташування роторів повинне мінятися при переході від знаку до знаку повідомлення.

Роторна машина складається з банку роторів і механізму для зміни положення роторів з кожним зашифрованим знаком, об'єднаного із пристроями введення й виведення.

Найпростіше з можливих рухів ротора – це рух за принципом одометра; воно використовувалося в німецькій машині Enigma під час Другої світової війни. При шифруванні одного знаку праве крайнє колесо повертається на одну позицію. Коли це (і будь-яке інше) колесо переміститься на m позицій і зробить повний оборот, колесо, розміщене ліворуч від нього, пересунеться на одну позицію, і процес буде повторюватися. Цей процес проведе банк роторів крізь всі його можливі положення, перш ніж цикл повториться. Оскільки всі ротори переміщаються з різними швидкостями, період n-роторної машини становить (при m = 26).

Для закону руху ротора бажані такі характеристики:

• період повинен бути більшим;

• після шифрування кожного знаку всі ротори або більша їхня частина повинні повернутися один щодо іншого.

Рух за принципом одометра оптимально в змісті першої вимоги, але зовсім незадовільно відносно другої вимоги. Поліпшення руху за принципом одометра можна одержати, якщо повертати кожен ротор більш ніж на одну позицію. Якщо зсуву кожного ротора не мають загальних множників з обсягом алфавіту m, то період залишиться максимальним.

Інше рішення полягає в обмеженні числа допустимих зупинних місць для кожного ротора за рахунок введення зовнішнього фіксуючого кільця, на якому певним способом зафіксовані місця зупинок. При використанні латинського алфавіту можна змусити машини повертатися та зупинятися в такий спосіб. Першому колесу дозволяється зупинятися в кожній з 26 позицій, другому колесу - тільки в 25 позиціях, третьому колесу - тільки в 23 позиціях і так далі до шостого колеса, якому дозволяється зупинятися тільки в 17 позиціях. Період такої роторної машини тепер становить 101 млн, а не 26⁶≈309 млн, як у випадку руху за принципом одометра. Втрата в довжині періоду з успіхом окупається отриманою складністю руху роторів. Тепер друга вимога задовольняється досить добре, оскільки кожне з коліс прокручується після шифрування кожного знаку і колеса можуть рухатися відносно одне до одного.

Роторна машина може бути настроєна за ключем зміною будь-яких її змінних:

• роторів;

• порядку розміщення роторів;

• числа місць зупинки на колесо;

• характеру руху і т. д.