Файл: PR_Avtomobilnye_dvigateli_kursovoy_--_2017-1.docx

4 Порядок выполнения динамического расчета кривошипно-шатунного механизма двигателя

Динамический расчет кривошипно-шатунного механизма проектируемого двигателя заключается в определении суммарных сил и моментов, возникающих от давления газов и сил инерции, что требуется для выполнения расчетов деталей двигателя на прочность и износостойкость, расчета подшипников коленчатого вала, анализа уравновешенности двигателя.

Динамический расчет проводится для номинального режима работы двигателя. В течение каждого рабочего цикла силы, действующие в КШМ, непрерывно изменяются по величине и направлению. Поэтому расчет необходимо производить для ряда положений коленчатого вала. Для четырехтактного двигателя силы определяются через каждые 30° угла поворота коленчатого вала в диапазоне от 0 до 720°, а в области резкого изменения величин нагрузок (от 360 до 390°) – через 15°. В качестве нулевого выбирается такое положение кривошипа, при котором поршень находится в верхней мертвой точке (в.м.т.) во время такта впуска.

Силы давления газов, действующие на площадь поршня, для упрощения заменяются одной силой Р_Г, направленной вдоль оси цилиндра и приложенной к оси поршневого пальца (рисунок 4.1). Сила Р_Г определяется для ряда значений угла  поворота коленчатого вала (рисунок 4.2) по действительной развернутой (в координатах Р – ) индикаторной диаграмме.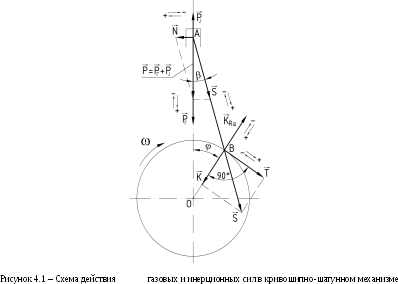

Построение развернутой диаграммы производится в следующей последовательности. На листе в координатах Р – V (Р – S) изображается полученная в тепловом расчете индикаторная диаграмма; затем правее ее наносится координатная сетка Р – , при этом ось абсцисс  по горизонтали должна располагаться на уровне линии Р₀ свернутой диаграммы (на развернутой диаграмме показывается не абсолютное давление Р_Г, а избыточное давление Р_Г над поршнем).

Дальнейшее перестроение индикаторной диаграммы осуществляется по методу Брикса: под свернутой диаграммой строится вспомогательная полуокружность и по формуле (2.71) определяется центр Брикса. Из центра О', от левой половины основания полуокружности под требуемыми углами  откладываются вспомогательные лучи, а из центра Брикса О₁ проводятся линии, параллельные этим лучам, до пересечения с полуокружностью. Из найденных таким образом точек проводятся вертикали, которые, пересекая диаграмму на участке, соответствующем требуемому такту двигателя, определяют положения поршня, при заданных значениях . Значения давлений в этих точках переносятся на вертикали соответствующих углов  развернутой диаграммы.

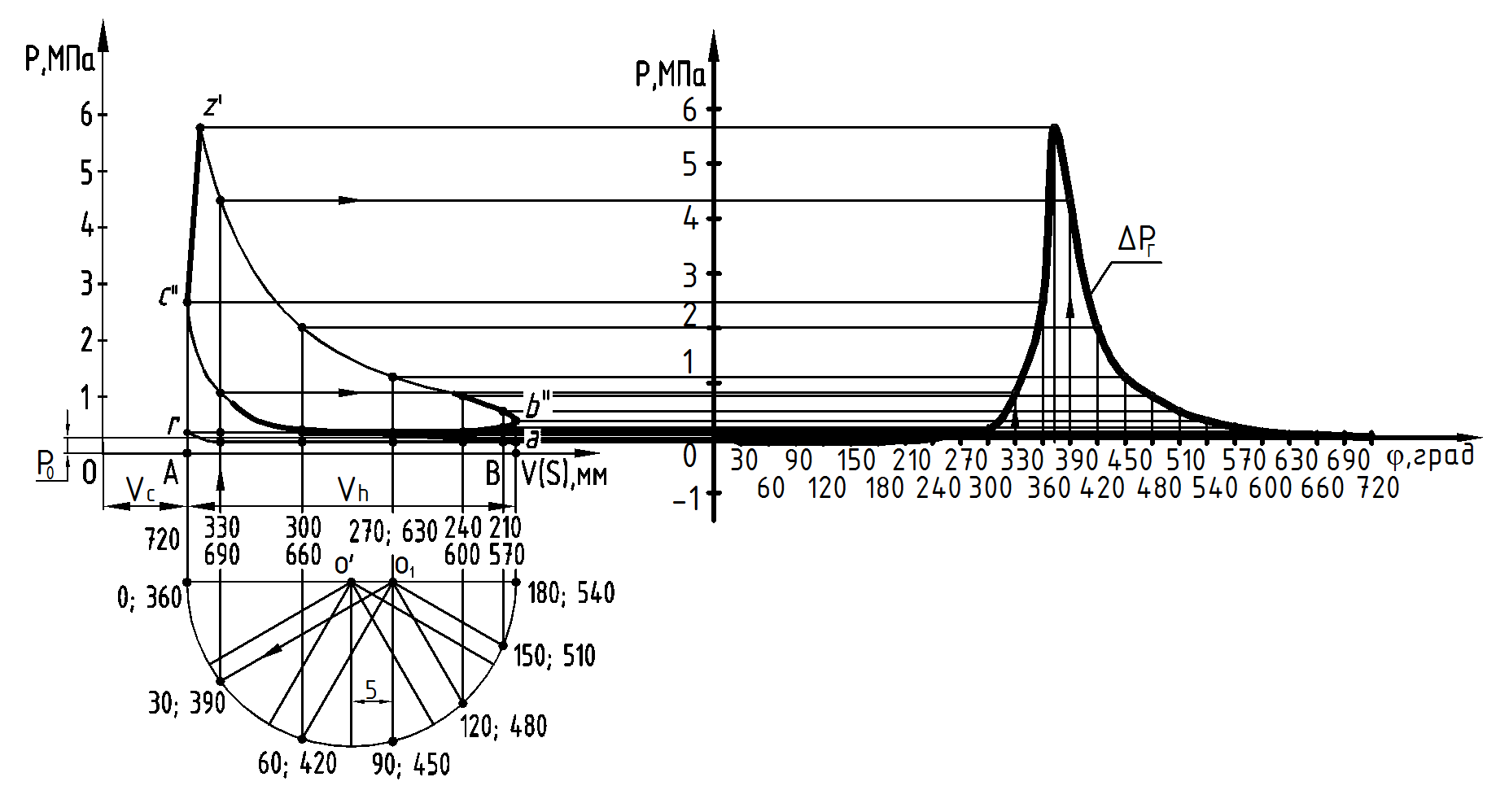
Рисунок 4.2 – Развертка индикаторной диаграммы в координатах Р – 

Удельная сила давления газов P_Г, МПа:

P_Г = р_Г / F_П = (Р – Р₀)  F_П / F_П = Р_Г, (4.1)

где Р – давление газов в любой момент времени, МПа;

F_П – площадь поршня, м². Причем

F_П = 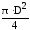. (4.2)

Величины Р_Г снимаются с развернутой индикаторной диаграммы для требуемых значений . Соответствующие им силы Р_Г рассчитываются по формуле (4.1). Силы давления газов, направленные к оси коленчатого вала, считаются положительными, а от него – отрицательными (на рисунке 4.1 стрелками указаны положительные и отрицательные направления).

4.1 Приведение масс частей кривошипно-шатунного механизма

Для упрощения динамического расчета действительный КШМ заменяется эквивалентной системой сосредоточенных масс (рисунок 4.3), которая состоит из массы m_J, совершающей возвратно-поступательное движение и сосредоточенной в точке А, и массы m_R, совершающей вращательное движение и сосредоточенной в точке В.

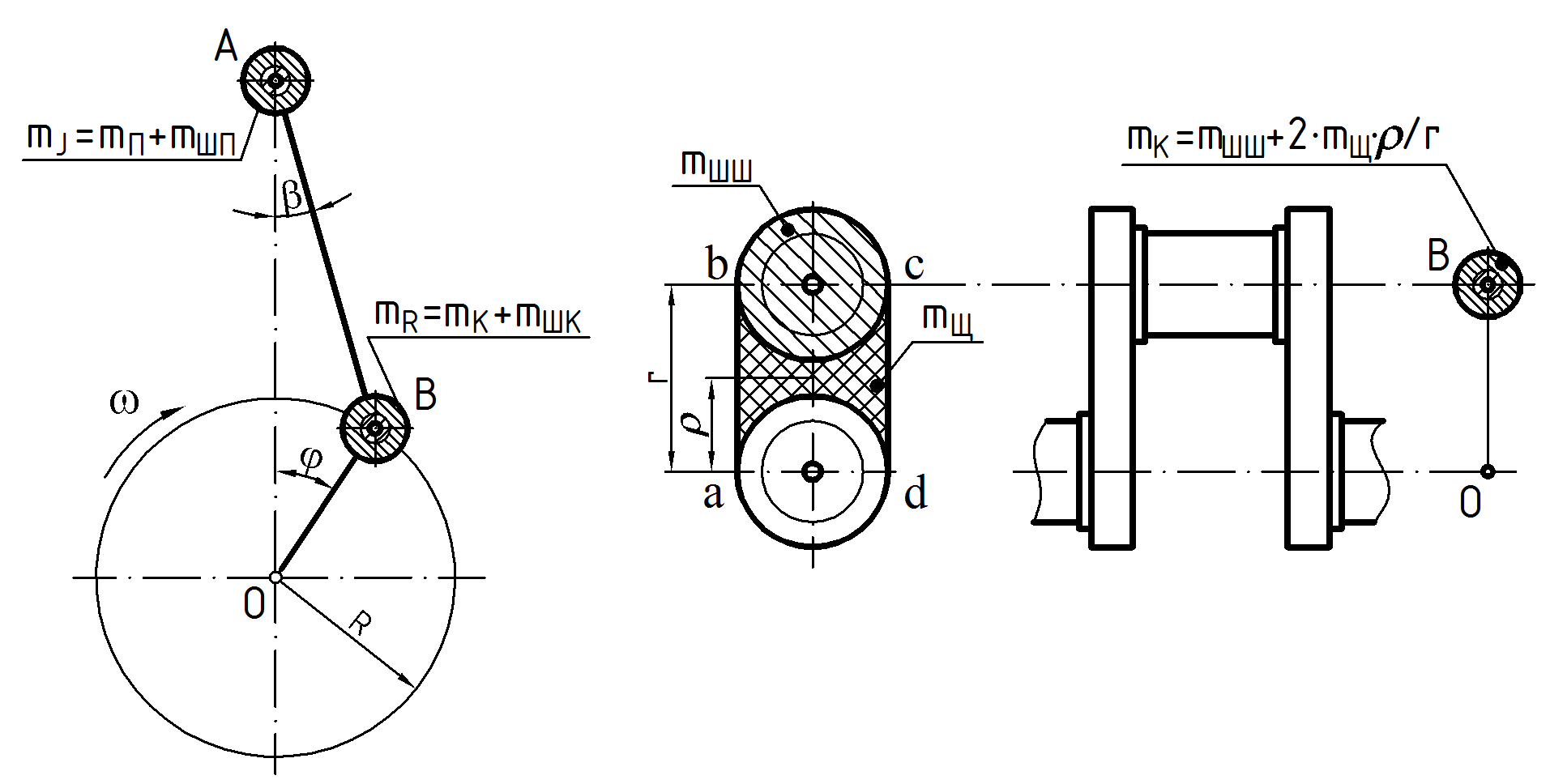
Рисунок 4.3 – Схемы системы сосредоточенных масс, динамически эквивалентной кривошипно-шатунному механизму

Сосредоточенные массы m_J, кг, и m_R, кг, находят по формулам:

m_J = m_П + m_ШП; m_R = m_К + m_ШК, (4.3)

где m_П – масса поршневой группы, кг;

m_ШП – часть массы шатунной группы, сосредоточенная в точке А (на оси поршневого пальца), m_ШП = 0,275  m_Ш;

m_ШК – часть массы шатунной группы, сосредоточенная в точке В (на оси кривошипа), m_ШК = 0,725  m_Ш;

m_К – часть массы кривошипа, сосредоточенная в точке В.

Полная масса шатунной группы m_Ш, кг:

m_Ш = m_ШП + m_ШК. (4.4)

Часть массы кривошипа m_К, кг, находят по формуле

m_К = m_ШШ + 2 m_Щ  /r, (4.5)

где m_ШШ – масса шатунной шейки с прилегающими частями щек, кг;

m_Щ – масса средней части щеки, заключенная в контуре abсd, центр тяжести которой расположен на расстоянии  от оси вращения вала.

Для приближенного определения значений m_П и m_Ш следует использовать конструктивные массы m_i' (массы, отнесенные к площади поршня), значения которых представлены в таблице 4.1, то есть по формулам:

m_П = m_П'  F_П; m_Ш = m_Ш'  F_П. (4.6)

Таблица 4.1 – Конструктивные массы элементов КШМ

При выборе значений из таблицы 4.1 следует учитывать, что большие значения m_i' соответствуют двигателям с большим диаметром цилиндров; уменьшение S/D снижает m_Ш' и m_К' ; V-образным двигателям с двумя шатунами на шейке соответствуют большие значения m_К'.

4.2 Расчет сил инерции

Силы инерции, действующие в КШМ, в соответствии с характером движения приведенных масс (см. рисунок 4.1) подразделяются на силы инерции поступательно движущихся масс Р_J и центробежные силы инерции вращающихся масс K_R.

Значение силы Р_J , Н, находят по формуле

Р_J = –m_J  j, (4.7)

где j – ускорение поршня, м/с². Причем

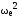
j = r  (cos  + λ  cos 2). (4.8)

Значение силы K_R, Н, находят по формуле

K_R = – m_R  r 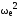. (4.9)

Для рядного двигателя центробежная сила инерции К_R является результирующей двух сил:

– силы инерции вращающихся масс шатуна К_RШ, Н:

К_RШ = – m_ШК  r 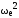; (4.10)

– силы инерции вращающихся масс кривошипа K_RK, Н:

K_RK = – m_К  r 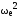. (4.11)

Силы инерции возвратно-поступательно движущихся масс Р_J действуют по оси цилиндра и, как силы давления газов, являются положительными, если направлены к оси коленчатого вала. Центробежная сила инерции K_R действует по радиусу кривошипа и направлена от оси коленчатого вала.

4.3 Расчет суммарных сил, действующих в кривошипно-шатунном механизме

Суммарная сила Р, МПа, действующая в КШМ, есть сумма удельных сил давления газов и сил возвратно-поступательно движущихся масс:

Р = Р_Г + Р_J. (4.12)

Суммарная сила Р, как и силы Р_Г и Р_J, направлена по оси цилиндра и приложена к оси поршневого пальца (см. рисунок 4.1). Воздействие от силы Р передается на стенки цилиндра перпендикулярно его оси и на шатун по направлению его оси.

Удельная нормальная сила N, МПа, действующая перпендикулярно оси цилиндра, воспринимается стенками цилиндра и ее значение равно:

N = Р  tg β, (4.13)

где β – угол отклонения шатуна от оси цилиндра, β = arcsin (λ  sin).