ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.02.2024
Просмотров: 630
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. Описание и классификация активных фильтров. Фильтр нижних частот.
4. Описание и классификация активных фильтров. Фильтр верхних частот.
5. Описание и классификация активных фильтров. Полосовые фильтры.
9. Генераторы гармонических сигналов. Теоретические сведения. Принцип работы. Генератор Буббы.
6 – 10 вопросы. Заключение по всем генераторам.
14. Принципы автоматического управления. Общие сведения о структурах систем управления. Регуляторы.
15. Электрический ток в вакууме. Вакуумный диод. Вакуумный триод.
), поскольку только в этом случае полосно-пропускающий фильтр будет работать достаточно эффективно.
Заграждающий RC-фильтр состоит из одного звена ФНЧ и одного звена ФВЧ, включенных параллельно.
Одиночный RC-фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области довольно часто используют многозвенные фильтры (см. ниже).
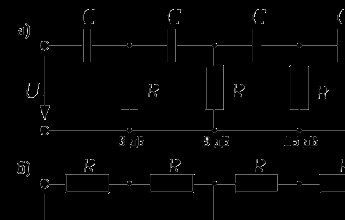
Частота среза многозвенного фильтра определяется по формуле ВЧ, НЧ RC-фильтра. Добавление каждого звена приводит к увеличению затухания на заданной частоте среза примерно на 6 дБ.
На рисунке а) – многозвенный ФВЧ, б) – многозвенный ФНЧ.
Сравнение пассивных фильтров с другими видами фильтров.
Достоинства пассивных фильтров: в качестве фильтрующих цепей, особенно в области низких частот (десятки килогерц и ниже), могут быть использованы различные схемы, образованные только из резисторов и емкостей (RC-цепи). В последнее время в связи с требованиями к микроминитюаризации электронной аппаратуры широко внедряются в практику RC-цепи, образованные не только дискретными R- и C-элементами, но и распределенными. Замена дискретных элементов распределенными приводит в ряде случаев не только к уменьшению габаритных размеров, но и к улучшению электрических характеристик фильтров. К достоинствам следует также отнести простоту конструкции фильтров и надежность.
К недостаткам пассивных фильтров следует отнести их большие масса габариты, особенно это относится к LC-фильтрам. Низкочастотные фильтры обычно никогда не делают на таких базисных элементах, так как здесь потребовались бы слишком громоздкие и дорогостоящие катушки индуктивности.
Назначение, классификация и принцип работы пассивных фильтров.
Электронный фильтр – это частотно-избирательное устройство, которое служит для передачи (пропускания) сигналов в заданном диапазоне частот (полосе пропускания) и подавления сигналов в других диапазонах частот (полоса задерживания). Фильтры широко используются в системах связи, в схемах защиты электронных систем от помех. Основное назначение фильтра состоит в том, чтобы исключить прохождение сигналов определенного диапазона частот и в то же время обеспечить передачу сигналов другого диапазона частот.
Функциональная схема трехфазного тиристорного выпрямителя показана ниже, одним из составляющих данной схемы является фильтр.

Различают аналоговые фильтры, в которых обрабатываемый сигнал имеет аналоговую форму, и цифровые фильтры, предназначенные для обработки цифровых сигналов. Рассмотрим аналоговые фильтры.
Фильтры делятся на активные и пассивные. Активные фильтры представляют собой частотно-избирательный усилительный каскад. К пассивным фильтрам относятся RC- и LC-фильтры. Фильтры также можно классифицировать исходя из диапазона частот, которые они пропускают или подавляют.
Существуют четыре типа фильтров:
1) Фильтр нижних частот, который пропускает все сигналы с частотой ниже некоторого заданного значения и подавляет сигналы более высоких частот.
2) Фильтр верхних частот, который пропускает все сигналы с частотой выше некоторого заданного значения и подавляет сигналы более низких частот.
3) Полосно-заграждающий фильтр (режекторный), который используется для подавления сигналов определенного диапазона частот, тогда как сигналы с частотами выше и ниже этого диапазона проходят беспрепятственно.
4) Полосно-пропускающий фильтр (полосовой), который пропускает сигналы заданной полосы частот и препятствует прохождению сигналов любых других частот.
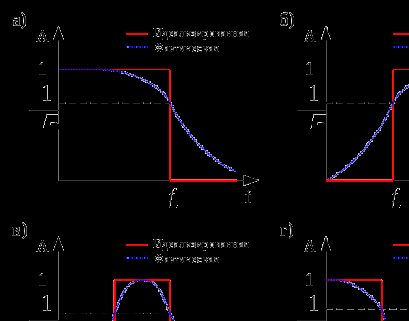
Амплитудно-частотные характеристики данных четырех типов фильтров представлены выше, где:
а) фильтр нижних частот;
б) фильтр верхних частот;
в) полосно-пропускающий фильтр;
г) полосно-заграждающий фильтр.
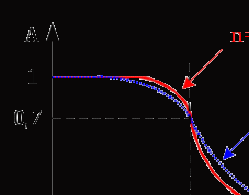
Частотой среза фильтра называют частоту, при которой амплитуда выходного сигнала составляет 1/√2 (≈0,71) от амплитуды входного сигнала или -3 дБ (по логарифмической шкале).
Передаточные функции аналоговых фильтров.
Аналоговый фильтр представляет линейную частотно-селективную цепь, поведение которой определяется операторной передаточной функцией H(p). Операторная передаточная функция – отношение изображений по Лапласу выходного и входного сигналов (см. выражение (1)), где U1(p) и U2(p) – изображения напряжений на входе и выходе фильтра, р – комплексная частотная переменная.
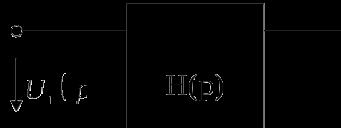
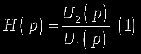
Известно, что передаточная функция линейной цепи является дробно-рациональной, т. е. представляет отношение двух полиномов от комплексной переменной р (см. выражение (2)).
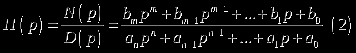
Полагая в (2) p = jω, получаем комплексную передаточную функцию, определяющую реакцию фильтра на гармоническое воздействие (см. выражение (3)).
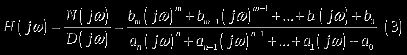
Представим передаточную функцию в показательной форме (см. выражение (4)).
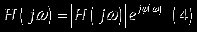
Модуль комплексной передаточной функции – амплитудно-частотная характеристика, а ее аргумент – фазочастотная характеристика.
Операторная передаточная функция H(p). Числитель и знаменатель H(p) можно записать в виде произведения сомножителей первого порядка в соответствии с выражением (5).
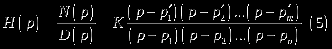
Корни полинома числителя называют нулями, а корни полинома знаменателя – полюсами передаточной функции. Расположение полюсов и нулей H(p) на комплексной плоскости определяет поведение цепи как в частотной, так и во временной областях. В частности, от расположения полюсов и нулей зависит форма частотных характеристик фильтра. Как правило, нули передачи частотно-селективных фильтров расположены на мнимой оси, включая начало координат и бесконечность.
В простейших случаях нули передачи расположены в начале координат (ФВЧ) или в бесконечности (ФНЧ). Такие фильтры имеют меньшую селективность, чем фильтры с нулями передачи на мнимой оси. Однако уменьшение селективности окупается значительным упрощением структуры цепи, реализующей передаточную функцию с нулями в начале координат или бесконечности.
В общем случае для получения передаточной функции, обеспечивающей заданную форму частотных характеристик, используют методы оптимизации. На практике часто используют типовые передаточные функции, имеющие аналитическое решение. Перечислим наиболее распространенные передаточные функции, аппроксимирующие АЧХ фильтра нижних частот:
Порядок передаточной функции n выбирают из условия обеспечения требуемого затухания в полосе задерживания на частоте ω > ωс:
Описание LC-фильтров.
Фильтры более высокого качества реализуются на основе катушек индуктивности и конденсаторов. В LC-фильтр могут входить также и резисторы. Связь входной и выходной цепей большинства LC-фильтров соответственно с источником сигнала и с нагрузкой производится таким образом, чтобы значения их реактивных или полных сопротивлений были равны.
Ниже представлена схема и АЧХ типового Г-образного LC-фильтра нижних частот.
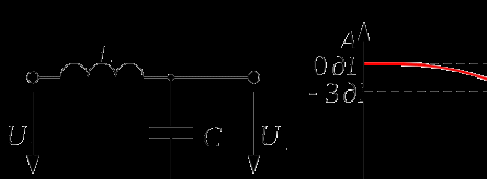
Расчет такого фильтра производится по формуле (1).
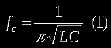
Все LC-фильтры обладают тем преимуществом, что на переменном токе конденсаторы и катушки индуктивности работают взаимообратно, т.е. при увеличении частоты сигнала индуктивное сопротивление возрастает, а емкостное падает. Таким образом, в
LC-фильтре нижних частот реактивное сопротивление параллельного элемента при увеличении частоты сигнала уменьшается, и этот элемент шунтирует высокочастотные сигналы. На низких частотах реактивное сопротивление параллельного элемента достаточно высокое. Последовательный элемент обеспечивает прохождение низкочастотных сигналов, а для сигналов высоких частот его реактивное сопротивление велико.
Простой Г-образный фильтр не обеспечивает достаточную крутизну амплитудно-частотной характеристики. Для увеличения крутизны в основную Г-образную структуру вводят дополнительную катушку индуктивности, как показано на рисунке. Такой фильтр называется Т-образным.
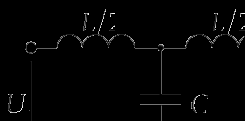
В Т-образном фильтре значение емкости конденсатора С такое же, как и в исходной Г-образной структуре, и все ее расчетные формулы сохраняются. Суммарная индуктивность катушек должна быть эквивалентна индуктивности единственной катушки исходной Г-образной структуры. Обычно требуемая общая индуктивность распределяется между двумя этими катушками поровну таким образом, чтобы каждая из катушек в Т-образном фильтре нижних частот имела индуктивность в два раза меньше, чем катушка в Г-образном фильтре.
Крутизну амплитудно-частотной характеристики можно увеличить также путем введения в цепь дополнительного конденсатора. Такой фильтр называется П-образным (схема представлена ниже).
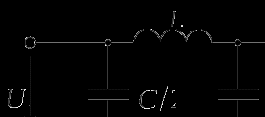
В П-образном фильтре значение индуктивности L такое же, как и в исходной Г-образной структуре, тогда как суммарная емкость конденсаторов должна быть эквивалентна емкости конденсатора исходной Г-образной структуры. Обычно требуемая общая емкость распределяется между двумя этими конденсаторами поровну таким образом, чтобы каждый из конденсаторов в П-образном фильтре имел емкость, равную половине емкости конденсатора в Г-образном фильтре.
Ниже представлена схема и АЧХ типового Г-образного LС-фильтра верхних частот.
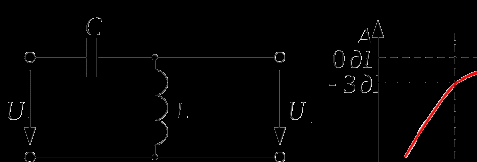
Расчет Г-образного LС-фильтра верхних частот производится по формуле (2).
Заграждающий RC-фильтр состоит из одного звена ФНЧ и одного звена ФВЧ, включенных параллельно.
Одиночный RC-фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области довольно часто используют многозвенные фильтры (см. ниже).

Частота среза многозвенного фильтра определяется по формуле ВЧ, НЧ RC-фильтра. Добавление каждого звена приводит к увеличению затухания на заданной частоте среза примерно на 6 дБ.
На рисунке а) – многозвенный ФВЧ, б) – многозвенный ФНЧ.
Сравнение пассивных фильтров с другими видами фильтров.
Достоинства пассивных фильтров: в качестве фильтрующих цепей, особенно в области низких частот (десятки килогерц и ниже), могут быть использованы различные схемы, образованные только из резисторов и емкостей (RC-цепи). В последнее время в связи с требованиями к микроминитюаризации электронной аппаратуры широко внедряются в практику RC-цепи, образованные не только дискретными R- и C-элементами, но и распределенными. Замена дискретных элементов распределенными приводит в ряде случаев не только к уменьшению габаритных размеров, но и к улучшению электрических характеристик фильтров. К достоинствам следует также отнести простоту конструкции фильтров и надежность.
К недостаткам пассивных фильтров следует отнести их большие масса габариты, особенно это относится к LC-фильтрам. Низкочастотные фильтры обычно никогда не делают на таких базисных элементах, так как здесь потребовались бы слишком громоздкие и дорогостоящие катушки индуктивности.
2. Назначение, классификация и принцип работы пассивных фильтров. Передаточные функции аналоговых фильтров. Описание LC-фильтров. Сравнение пассивных фильтров с другими видами фильтров.
Назначение, классификация и принцип работы пассивных фильтров.
Электронный фильтр – это частотно-избирательное устройство, которое служит для передачи (пропускания) сигналов в заданном диапазоне частот (полосе пропускания) и подавления сигналов в других диапазонах частот (полоса задерживания). Фильтры широко используются в системах связи, в схемах защиты электронных систем от помех. Основное назначение фильтра состоит в том, чтобы исключить прохождение сигналов определенного диапазона частот и в то же время обеспечить передачу сигналов другого диапазона частот.
Функциональная схема трехфазного тиристорного выпрямителя показана ниже, одним из составляющих данной схемы является фильтр.

Различают аналоговые фильтры, в которых обрабатываемый сигнал имеет аналоговую форму, и цифровые фильтры, предназначенные для обработки цифровых сигналов. Рассмотрим аналоговые фильтры.
Фильтры делятся на активные и пассивные. Активные фильтры представляют собой частотно-избирательный усилительный каскад. К пассивным фильтрам относятся RC- и LC-фильтры. Фильтры также можно классифицировать исходя из диапазона частот, которые они пропускают или подавляют.
Существуют четыре типа фильтров:
1) Фильтр нижних частот, который пропускает все сигналы с частотой ниже некоторого заданного значения и подавляет сигналы более высоких частот.
2) Фильтр верхних частот, который пропускает все сигналы с частотой выше некоторого заданного значения и подавляет сигналы более низких частот.
3) Полосно-заграждающий фильтр (режекторный), который используется для подавления сигналов определенного диапазона частот, тогда как сигналы с частотами выше и ниже этого диапазона проходят беспрепятственно.
4) Полосно-пропускающий фильтр (полосовой), который пропускает сигналы заданной полосы частот и препятствует прохождению сигналов любых других частот.

Амплитудно-частотные характеристики данных четырех типов фильтров представлены выше, где:
а) фильтр нижних частот;
б) фильтр верхних частот;
в) полосно-пропускающий фильтр;
г) полосно-заграждающий фильтр.
Частотой среза фильтра называют частоту, при которой амплитуда выходного сигнала составляет 1/√2 (≈0,71) от амплитуды входного сигнала или -3 дБ (по логарифмической шкале).
Передаточные функции аналоговых фильтров.
Аналоговый фильтр представляет линейную частотно-селективную цепь, поведение которой определяется операторной передаточной функцией H(p). Операторная передаточная функция – отношение изображений по Лапласу выходного и входного сигналов (см. выражение (1)), где U1(p) и U2(p) – изображения напряжений на входе и выходе фильтра, р – комплексная частотная переменная.
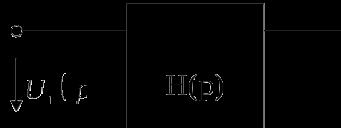
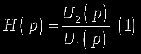
Известно, что передаточная функция линейной цепи является дробно-рациональной, т. е. представляет отношение двух полиномов от комплексной переменной р (см. выражение (2)).
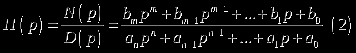
Полагая в (2) p = jω, получаем комплексную передаточную функцию, определяющую реакцию фильтра на гармоническое воздействие (см. выражение (3)).
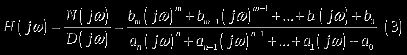
Представим передаточную функцию в показательной форме (см. выражение (4)).
Модуль комплексной передаточной функции – амплитудно-частотная характеристика, а ее аргумент – фазочастотная характеристика.
Операторная передаточная функция H(p). Числитель и знаменатель H(p) можно записать в виде произведения сомножителей первого порядка в соответствии с выражением (5).
Корни полинома числителя называют нулями, а корни полинома знаменателя – полюсами передаточной функции. Расположение полюсов и нулей H(p) на комплексной плоскости определяет поведение цепи как в частотной, так и во временной областях. В частности, от расположения полюсов и нулей зависит форма частотных характеристик фильтра. Как правило, нули передачи частотно-селективных фильтров расположены на мнимой оси, включая начало координат и бесконечность.
В простейших случаях нули передачи расположены в начале координат (ФВЧ) или в бесконечности (ФНЧ). Такие фильтры имеют меньшую селективность, чем фильтры с нулями передачи на мнимой оси. Однако уменьшение селективности окупается значительным упрощением структуры цепи, реализующей передаточную функцию с нулями в начале координат или бесконечности.
В общем случае для получения передаточной функции, обеспечивающей заданную форму частотных характеристик, используют методы оптимизации. На практике часто используют типовые передаточные функции, имеющие аналитическое решение. Перечислим наиболее распространенные передаточные функции, аппроксимирующие АЧХ фильтра нижних частот:
-
Фильтр Баттерворта с максимально плоской амплитудно-частотной характеристикой. -
Фильтр Чебышева с равноволновой характеристикой в полосе пропускания. -
Инверсный фильтр Чебышева с равноволновой характеристикой в полосе задерживания. -
Эллиптический фильтр, имеющий равноволновые характеристики в полосе пропускания и полосе задерживания. -
Фильтр Бесселя с фазочастотной характеристикой, близкой к линейной.
Порядок передаточной функции n выбирают из условия обеспечения требуемого затухания в полосе задерживания на частоте ω > ωс:

Описание LC-фильтров.
Фильтры более высокого качества реализуются на основе катушек индуктивности и конденсаторов. В LC-фильтр могут входить также и резисторы. Связь входной и выходной цепей большинства LC-фильтров соответственно с источником сигнала и с нагрузкой производится таким образом, чтобы значения их реактивных или полных сопротивлений были равны.
Ниже представлена схема и АЧХ типового Г-образного LC-фильтра нижних частот.

Расчет такого фильтра производится по формуле (1).
Все LC-фильтры обладают тем преимуществом, что на переменном токе конденсаторы и катушки индуктивности работают взаимообратно, т.е. при увеличении частоты сигнала индуктивное сопротивление возрастает, а емкостное падает. Таким образом, в
LC-фильтре нижних частот реактивное сопротивление параллельного элемента при увеличении частоты сигнала уменьшается, и этот элемент шунтирует высокочастотные сигналы. На низких частотах реактивное сопротивление параллельного элемента достаточно высокое. Последовательный элемент обеспечивает прохождение низкочастотных сигналов, а для сигналов высоких частот его реактивное сопротивление велико.
Простой Г-образный фильтр не обеспечивает достаточную крутизну амплитудно-частотной характеристики. Для увеличения крутизны в основную Г-образную структуру вводят дополнительную катушку индуктивности, как показано на рисунке. Такой фильтр называется Т-образным.

В Т-образном фильтре значение емкости конденсатора С такое же, как и в исходной Г-образной структуре, и все ее расчетные формулы сохраняются. Суммарная индуктивность катушек должна быть эквивалентна индуктивности единственной катушки исходной Г-образной структуры. Обычно требуемая общая индуктивность распределяется между двумя этими катушками поровну таким образом, чтобы каждая из катушек в Т-образном фильтре нижних частот имела индуктивность в два раза меньше, чем катушка в Г-образном фильтре.
Крутизну амплитудно-частотной характеристики можно увеличить также путем введения в цепь дополнительного конденсатора. Такой фильтр называется П-образным (схема представлена ниже).
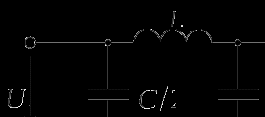
В П-образном фильтре значение индуктивности L такое же, как и в исходной Г-образной структуре, тогда как суммарная емкость конденсаторов должна быть эквивалентна емкости конденсатора исходной Г-образной структуры. Обычно требуемая общая емкость распределяется между двумя этими конденсаторами поровну таким образом, чтобы каждый из конденсаторов в П-образном фильтре имел емкость, равную половине емкости конденсатора в Г-образном фильтре.
Ниже представлена схема и АЧХ типового Г-образного LС-фильтра верхних частот.

Расчет Г-образного LС-фильтра верхних частот производится по формуле (2).
