Файл: Практикум Моделирование систем в среде AnyLogic 8.doc

Рис. 5.1. Популяция агентов



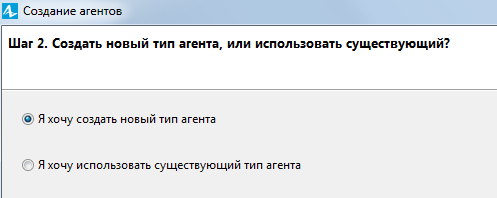
Рис. 5.2. Выбор типа агента

Затем следует указать, что создается новый тип агента (рисунок 5.2). Затем нужно нажать кнопку «Далее». На втором шаге задают имя новому агенту Peoples, а имя популяции как peoples (рисунок 5.3). Затем нужно нажать кнопку «Далее».



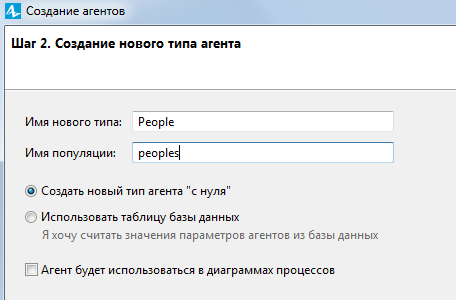
Рис. 5.3. Агент и популяция

На третьем шаге следует выбрать режим анимации агентов как 2D и из раздела «Основные» указать пиктограмму «Человек» (рисунок 5.4).



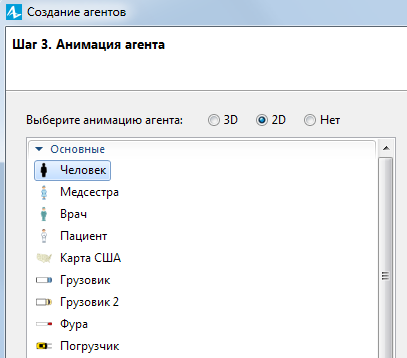
Рис.5.4. Задание свойств агента.

Затем на следующем шаге нужно задать параметр агенту AdEffectiveness – интенсивность совершения покупок агентом под действием рекламы. Параметр задается равным 0,01 (рисунок 5.5).



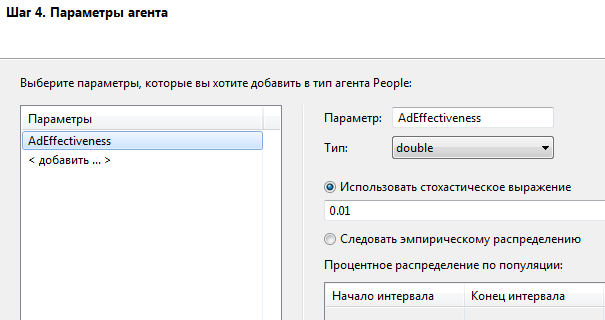
Рис. 5.5. Задание свойств пространства агентов

На следующем шаге нужно задать численность популяции. Для данной модели примем это значение равным 50 агентам (рисунок 5.6).



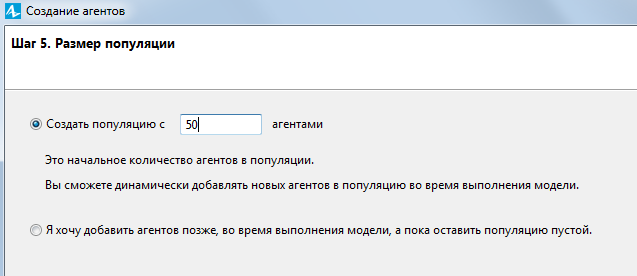
Рис.5.6. Число агентов

На заключительном шаге выбирают параметры агентного пространства. Это среда обитания популяции агентов. Агентное пространство должно быть непрерывным. Размер пространства 500 на 500 модельных единиц. Агенты располагаются в пространстве случайным образом (рисунок 5.7).



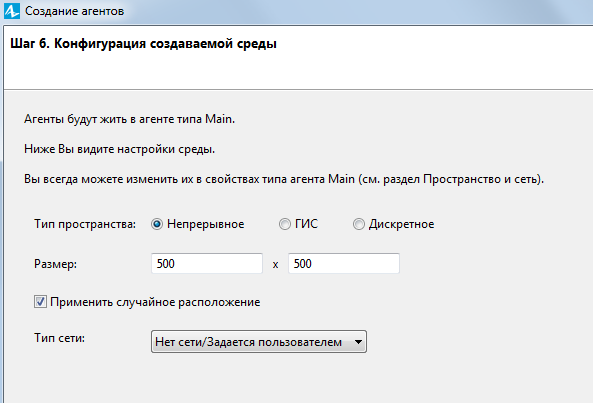
Рис. 5.7. Настройка агентного пространства

В результате в поле агента Main будет создана популяция агентов, так как это показано на рисунке 5.8.



Рис. 5.8. Созданная популяция агентов

Для корректного вывода популяции агентов при работе модели следует выделить в поле агента Main пиктограмму агента People и указать режим вывода агентов «Рисовать со сдвигом от данной точки» (рисунок 5.10).

---

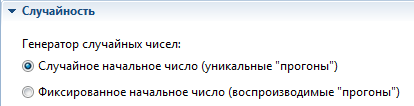
Рис. 5.9. Настройка эксперимента.

Сохраните модель и выполните запуск модели. Вид агентного пространства должен соответствовать рисунку 5.11. Чтобы расположение агентов изменялось при новом запуске модели следует настроить эксперимент так как это показано на рисунке 5.9.



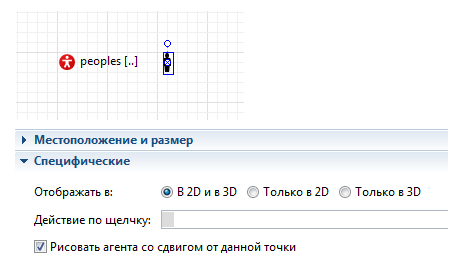
Рис. 5.10. Правило вывода агентов



Рис. 5.11. Популяция агентов при работе модели

---

5.2. Поведение агентов

Поведение агента определяется его конечным автоматом – стейтчартом. На дереве проекта выберите агента People. Постройте конечный автомат, так как это показано на рисунке 5.12.



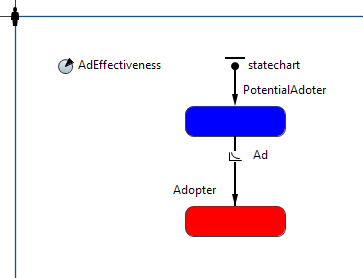
Рис.5.12. Конечный автомат агента.

Стейтчарт агента состоит из двух состояний:

PotentialAdopter – состояние потенциального покупателя товара;

Adopter – состояние покупки товара.

Цвет заливки состояния PotentialAdopter – синий, а состояния Adoter – красный.

Действие при входе для состояния PotentialAdopter:

shapeBody.setFillColor(blue);

Потенциальные потребители будут отображаться синим цветом.

Действие при входе для состояния Adopter:

shapeBody.setFillColor(red);

Потребители товара будут отображаться красным цветом.

Переход выполняется с заданной интенсивностью равной параметру AdEffetiveness. Единица измерения интенсивности «в день».

Далее следует добавить функции для вычисления статистических показателей по популяции агентов. В поле агента Main выберите популяцию peoples и введите статистические функции для вычисления число потенциальных потребителей и числа потребителей товара (рисунок 5.13).



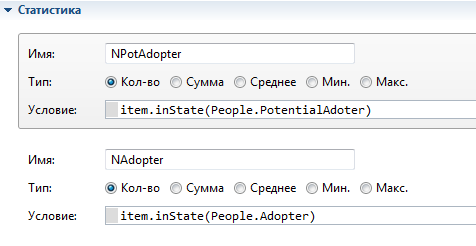
Рис. 5.13. Статистические функции

Описание созданных статистических функций приводится в таблице 5.1.

Таблица 5.1

Функции сбора статистики

Имя	Действие	Условие
NPotAdopter	Подсчет количества потенциальных потребителей	item.inState(People.PotentialAdopter);
NAdopter	Подсчет количества потребитилей	item.inState(People.Adopter);

Подсчет количества выполняется при входе в активности соответствующего состояния объекта statechart методом:

public boolean inState(short state)

Где: item – указатель на текущий реплицированный объект, который используется при подсчете AnyLogic статистического показателя.


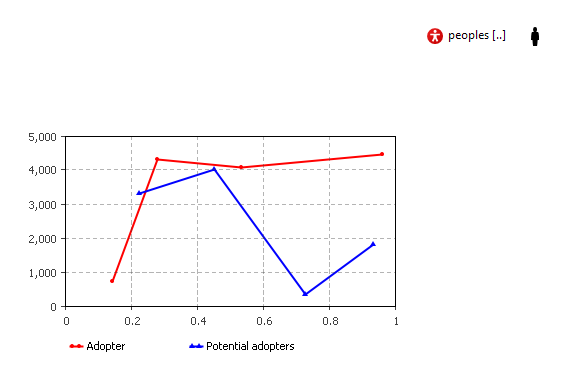
Рис. 5.14. Временной график модели; Adopter – число потребителей товара; Potential adopters – число потенциальных потребителей товара

---

Разместите в поле корневого объекта временной график для вывода статистических показателей (рисунок 5.14). Масштаб графика – временной диапазон один год. Единица измерения обновления данных дни. Период обновления один день, отображать 365 дней.

Настройте эксперимент модели так, что бы остановка произошла при достижении значения равного 365 дней.

Вид графика, после запуска модели показан на рисунке 5.15.



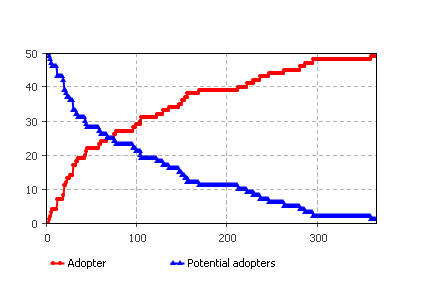
Рис.5.15. Продажа под действием рекламы

5.3. Учет влияния общения между потребителями

Требуется учесть в модели продаж влияния общения между потребителями продукта на покупку товара.

Откройте агент People и измените его стейтчарт в соответствии с рисунком 5.16.



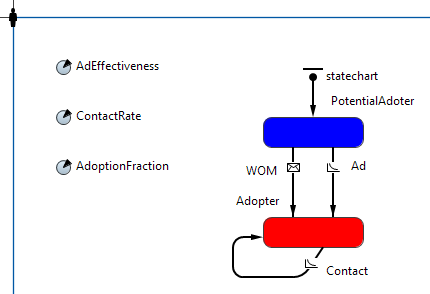
Рис.5.16. Учет общения потребителей

Для учета общения потребителей нужно добавить в модель два параметра ContactRate=5 (интенсивность контактов), AdoptionFraction=0.01 (вероятность покупки потенциальными потребителями продукта).

Переход Contact моделирует общение потребителей. Он происходит с интенсивностью равной ContactRate. При этом должно формироваться сообщение о желании купить продукт. Такое действие моделируется с помощью оператора AnyLogic

sendToRandom("buy");

Единица измерения интенсивности срабатывания перехода – дни.

Выполнение перехода WOM моделирует покупка товара потенциальным покупателем, он происходит при получении сообщения "buy" символьного типа String. Что бы моделировать случайный характер покупок введем дополнительное условие по параметру AdoptionFraction, используя функцию randomTrue(AdoptionFraction). Функция возвращает значение true с заданной вероятностью AdoptionFraction.



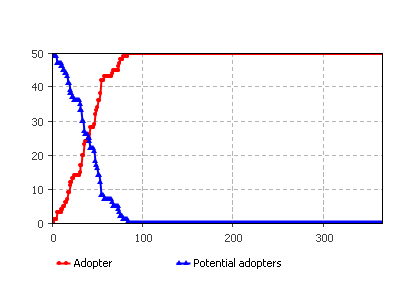
Рис.5.17. Учет общения потребителей

Протестируйте модель. график динамических процессов должен соответствовать рисунку 5.17.

5.4. Контрольное задание «Учет повторных покупок агентами»

Дополните модель покупок, таким образом, чтобы в ней учитывались повторные покупки товара по истечению контрольного срока его службы DiscardTime=2 (месяцы).

Методическое указание: в рамках модели агентов

---

, повторная покупка это переход потребителя в разряд потенциальных покупателей c интенсивностью DiscardTime.

Вид динамических процессов должен соответствовать рисунку 5.18



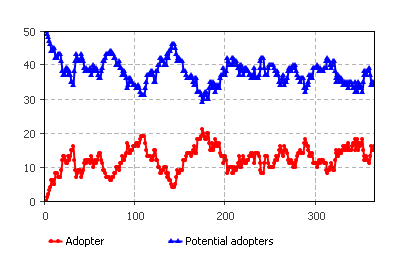
Рис.5.18. Динамика процессов с учетом повторных покупок

---