Файл: Первый. Земля как средство производства в сельском хозяйстве.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 134
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Элементами данной системы координат являются (рис.6): ось Оx, направление которой принимается параллельным истинному магнитному или осевому меридиану зоны либо произвольным; ось Оy, перпендикулярная к оси Ох; точка 0 – начало координат.
Осями координат горизонтальная плоскость делится на четыре четверти. В отличие от принятой в математике левой системы плоских прямоугольных (декартовых) координат в геодезии применяется правая система прямоугольных координат, в которой нумерация четвертей ведется по ходу часовой стрелки, начиная с северо-восточной четверти; это позволяет использовать в геодезических вычислениях формулы тригонометрии без каких-либо изменений.
Положение любой точки на плоскости в данной системе определится координатами х, у; их знаки зависят от четверти, в которой находится точка. Координаты точек, например А и В (xА, yА, хВ, yВ), равны соответственно расстояниям от начала координат до проекции этих точек на оси Ох и Оу.
Проекции линии АВ на оси 0x и 0у называются приращениями координат и обозначаются ?x, ?y. Знаки приращений также зависят от четверти; если направления приращений координат – катетов прямоугольных треугольников – совпадают (рис. 6) с положительным направлением координатных осей, то приращения координат будут положительны, если не совпадают, то приращения отрицательны.
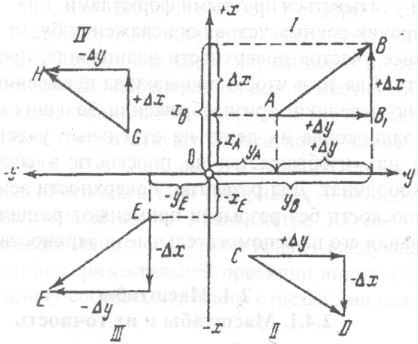
Рис. 6. Плоская условная система прямоугольных координат
Знаки приращений координат по четвертям показаны на рис. 6. Если известны координаты хА, yА точки А и приращения координат ?x, ?у между точками А и В, то координаты точки В будут равны:
Данная система координат применяется при горизонтальных съемках и составлении планов местности.
Зональная система плоских прямоугольных координат. При топографических съемках, маркшейдерских и инженерно-геодезических работах наиболее целесообразно применять системы плоских прямоугольных координат. Поэтому для изображения на плоскости значительных территорий земной поверхности применяются картографические проекции, дающие возможность переносить точки с поверхности эллипсоида на плоскость по определенным математическим законам. В общем случае картографические проекции вызывают искажения как углов, так и длин.
В геодезии выгодно применять такие проекции эллипсоида на плоскость, которые не искажали бы углов. Подобные проекции называются равноугольными или конформными. Возникающие при этом искажения длин и площадей должны быть незначительными и учитываться простыми формулами.
При прочих равных условиях искажения будут тем больше, чем обширнее участок поверхности эллипсоида, проектируемый на плоскость. Для того чтобы поправки за искажение длин были сравнительно невелики, при изображении больших областей поверхности эллипсоида их делят на отдельные участки (зоны) и каждый из них изображается на плоскости в системе прямоугольных координат. Для развертки поверхности земного эллипсоида на плоскость без разрывов применяют различные методы проектирования его на вспомогательные поверхности.
2.4. Масштабы
2.4.1. Масштабы и их точность
При составлении планов и карт горизонтальные проекции линий местности уменьшают в определенное число раз в зависимости от требований и точности, предъявляемых к планам и картам.
Степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте называется масштабом. Иными словами, масштаб есть отношение длины отрезка s на плане или карте к горизонтальной проекции соответствующего отрезка S на местности, т. е. s/S – масштаб. Различают численный и графический масштабы.
Численный масштаб. Численный масштаб - это правильная дробь, числитель которой есть единица, а знаменатель - число, показывающее, во сколько раз горизонтальные проекции линий местности уменьшены на плане или карте:
где М — знаменатель численного масштаба.
Чем больше значение знаменателя численного масштаба М, тем больше степень уменьшения горизонтальных проекций линий местности и тем мельче масштаб плана или карты. Численный масштаб — безразмерная величина, поэтому им можно пользоваться при измерениях в любых линейных мерах.
В геодезии наиболее часто применяются следующие масштабы: 1 : 500, 1 : 1000, 1 : 2000, 1 : 5000 – для планов и 1 : 10 000, 1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:300 000, 1:500 000, 1:1000 000 – для карт. Указанные отношения показывают, что горизонтальные проекции линий местности уменьшены на плане соответственно в 500, 1000, 2000 и т. д. раз, т. е. отрезку в 1 см на плане соответствуют на местности длины: 500 см или 5 м; 1000 см или 10 м; 2000 см или 20 м и т. д. На картах ниже подписи численного масштаба (например, 1:10 000) приводится пояснительный масштаб: «в 1 сантиметре 100 м».
При помощи масштабов можно решать следующие задачи:
1. По длине горизонтальной проекции линии S на местности определить длину соответствующего отрезка s на плане масштаба –
Пусть S = 275,5 м,
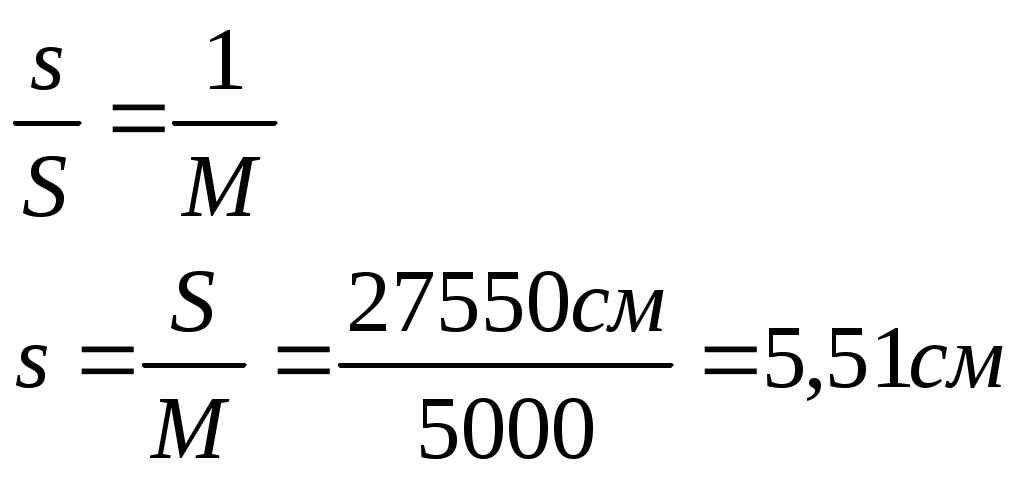
И
з соотношения находим s == 5,51 см.
Рис. 7. Масштабы:
а — линейный; б — поперечный
2. По длине отрезка s на плане масштаба определить длину линии S на местности.
Пусть s = 3,62 см, = 1 : 2000.
Тогда S = sM = 3,62 см ?2000 = 7240 см = 72,4 м.
При большом объеме работ для исключения вычислений в решении указанных задач удобнее пользоваться графическими масштабами, к которым относятся линейный и поперечный (трансверсальный) масштабы.
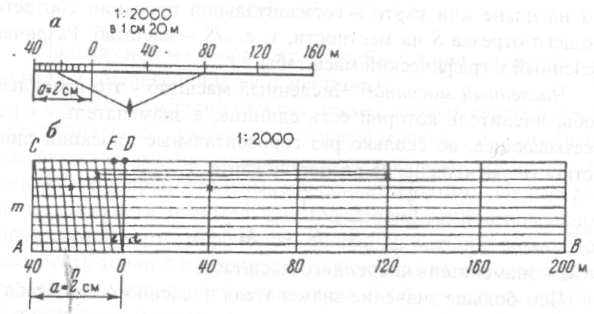
Линейный масштаб. Линейным масштабом называется графическое изображение численного масштаба в виде прямой линии с делениями для отсчета расстояний (рис. 7, а).
Для построения линейного масштаба на прямой линии откладывают ряд отрезков одинаковой длины а (например, а=2 см), называемой основанием линейного масштаба. Крайний левый отрезок делят на 10 равных частей и на правом его конце ставят 0, а на левом — число метров (километров), которое на плане соответствует основанию в заданном масштабе. Вправо от 0 деления масштаба подписывают значениями соответствующих расстояний на местности. Размерность ставится один раз в правом конце линейного масштаба.
На рис. 7, а показан линейный масштаб для численного масштаба 1:2000, на котором раствором циркуля-измерителя найден отрезок на плане, соответствующий линии местности S = 106 м. При этом десятые доли малого деления оцениваются на глаз. В связи с этим линейный масштаб во многих случаях не позволяет измерять расстояния с необходимой точностью.
Предельная и графическая точность масштабов. При оценке точности нанесения точек на план следует исходить из физиологических возможностей человеческого глаза. Как известно, глаз человека способен отчетливо различать две точки, если они располагаются под углом не менее 60" к наблюдателю. При меньшем угле зрения глаз воспринимает две точки слившимися в одну. Для расстояния наилучшего зрения, равного 25 см, углу в 60" соответствует отрезок, равный 0,1мм. Таков, например, диаметр кружка от укола остро отточенной иглы. Отсюда следует, что на плане (карте) в самом благоприятном случае можно изобразить лишь такие горизонтальные проекции линий местности, которым в данном масштабе соответствует отрезок 0,1 мм и более.
Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм на плане, называется предельной точностью масштаба tпр, т. е.
Практически принимается, что длина отрезка на плане или карте может быть оценена с точностью ±0,2 мм. Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм на плане, называется графической точностью масштаба tграф, т. е.
Значения предельной и графической точности различных численных масштабов, найденные по формулам (tпр) и (tграф), приведены ниже.

Такая точность определения расстояний на плане или карте не может быть достигнута при использовании линейного масштаба. Поэтому для повышения точности измерений расстояний на плане или карте применяют поперечный (трансверсальный) масштаб.
Поперечный масштаб. Поперечный масштаб является разновидностью линейного масштаба. Для его построения на отрезке прямой АВ (рис.7,б) несколько раз откладывают основание масштаба, равное обычно 2 см. В полученных точках восставляют перпендикуляры к линии АВ произвольной, но равной длины. Два крайних перпендикуляра делят на m равных частей и через одноименные точки проводят линии, параллельные прямой АВ. Левые нижнее АО и верхнее CD основания делят на п равных частей; точку О нижнего основания соединяют наклонной линией с первой точкой Е верхнего основания CD, а через все остальные точки проводят линии, параллельные ОЕ (трансверсали).
2.4.2. Понятие о плане, карте и профиле
Основным итогом топографо-геодезических работ является чертеж земной поверхности, составленный по определенным правилам и отвечающий установленным требованиям. Такими чертежами являются план, карта и профиль.
Из приведенного ранее видно, что при изображении небольшого участка земной поверхности (в пределах площади круга радиусом до 10 км) соответствующую ему часть уровенной поверхности можно принять за горизонтальную плоскость. Следовательно, при ортогональном проектировании точек земной поверхности на горизонтальную плоскость горизонтальные проекции линий и углов местности будут получены без искажений. Чертеж, дающий в уменьшенном и подобном виде изображение горизонтальной проекции небольшого участка местности, в пределах которого кривизна уровненной поверхности не учитывается, называется планом.
На плане могут изображаться ситуация и рельеф. Ситуацию местности составляет совокупность контуров и неподвижных местных предметов. К рельефу относятся неровности земной поверхности естественного происхождения.
Если на плане изображается только ситуация, то такой план называется ситуационным или контурным. Если кроме ситуации на плане изображается рельеф, то такой план называется топографическим. По плану можно решать различные задачи: измерять расстояния между точками местности, углы между заданными направлениями, площади участков земной поверхности, определять отметки точек, крутизну скатов и т. п. Точность решения указанных задач зависит от масштаба плана.
Имея топографический план, можно составить изображение вертикального разреза местности по заданному направлению, называемое профилем. Профиль характеризует рельеф по линии местности. План и профиль служат основными исходными документами при проектировании и строительстве инженерных сооружений.
2.4.3. Условные знаки планов и карт
Важнейшим показателем качества топографических карт и планов наряду с точностью является их наглядность. Она достигается применением условных знаков, с помощью которых на картах и планах изображаются ситуация и рельеф местности. Условные знаки, изображающие ситуацию местности, подразделяются на площадные, внемасштабные, линейные и пояснительные.
Площадные или масштабные условные знаки служат для изображения объектов, занимающих значительную площадь и выражающихся в масштабе карты или плана. Площадный условный знак состоит из границы объекта и заполняющих его знаков или условной окраски. Контур объекта показывается точечным пунктиром (контур леса, луга, болота), сплошной линией (контур водоема, населенного пункта). Заполняющие знаки располагаются внутри контура в определенном порядке (произвольно, в шахматном порядке, горизонтальными и вертикальными рядами). Площадные условные знаки позволяют не только найти расположение объекта, но и оценить его линейные размеры, площадь и очертания (рис.8.).

Рис.8. Условные знаки и обозначения
Внемасштабными называются такие условные знаки, которыми предметы местности изображаются без соблюдения масштаба карты или плана (колодец). Эти знаки не позволяют судить о размерах изображаемых местных предметов.

