Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях, и все массы положительны, это, тем не менее, очень важная сила во Вселенной. В частности, электромагнитное взаимодействие между телами в космических масштабах мало, поскольку полный электрический заряд этих тел равен нулю (вещество в целом электрически нейтрально).

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

2. 
   Гравитационное поле в общей теории относительности.
   

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала), иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем — метрикой четырёхмерного пространства-времени, а напряжённость гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой.

Стандартной задачей ОТО является определение компонента метрического тензора пространства, определяющего его кривизну, в совокупности задающих геометрические свойства пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырёхмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием её формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка.

---

Известно, что в ОТО имеются затруднения в связи с неинвариантностью энергии гравитационного поля, то есть с несохранением сущностных отношений при изменении других характеристик, поскольку данная энергия не описывается тензором и может быть теоретически определена разными способами. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия (так как спин протяжённого объекта также не имеет однозначного определения). Считается, что существуют определённые проблемы с однозначностью результатов и обоснованием непротиворечивости (проблема гравитационных сингулярностей).
Гравитационная сингулярность представляет собой точку в пространстве и времени, сквозь которую нельзя провести геодезическую линию.
Величины (например, скалярная кривизна или плотность энергии), характеризующие гравитационное поле, при рассмотрении гравитационной сингулярности становятся неопределенными или бесконечными . Согласно теории Альберта Эйнштейна, сингулярность появляется при образовании черной дыры, и ее нельзя обнаружить в том случае, если она находится за горизонтом событий.  Что касается Большого взрыва, то при нем была голая сингулярность, которую можно было бы "увидеть", если оказаться недалеко. Но, поскольку в современной физике сингулярность описывается только как теоретический объект, то и не было бы возможным наблюдать ее в реальности.

Пространство-время ОТО представляет собой псевдориманово многообразие - многообразие, в котором задан метрический тензор,
невырожденный в каждой точке с переменной метрикой. Причиной искривления пространства-времени является присутствие материи, и чем больше её энергия, тем искривление сильнее. Для определения метрики пространства-времени при известном распределении материи надо решить уравнения Эйнштейна.



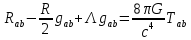
Где 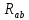, ,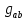 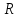– характеристики пространства,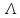

---

– космологическая постоянная - физическая постоянная, характеризующая свойства вакуума, 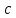– скорость света, 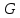– гравитационная постоянная, 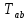– тензор энергии импульса.

Ньютоновская же теория тяготения представляет собой приближение ОТО, которое получается, если учитывать только «искривление времени», то есть изменение временной компоненты метрики. Распространение возмущений гравитации, то есть изменений метрики при движении тяготеющих масс, происходит с конечной скоростью, и дальнодействие в ОТО отсутствует.

Другие существенные отличия гравитационного поля ОТО от ньютоновского: возможность нетривиальной топологии пространства, особых точек, гравитационные волны.

Концепция пространства и времени в ОТО:

• 
  Пространство-время оказываются локально (вблизи массивных тел) искривленными;
  
• 
  Вся материя, рассеянная в космосе, вносит вклад в гравитационное поле и, тем самым, в кривизну пространства и времени;
  
• 
  Форма пространства-времени меняется не мгновенно, как в теории Ньютона, а со скоростью c.
  

3. 
   Теория Эйнштейна — Картана
   

Теория Эйнштейна — Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Кривизна пространства-времени при этом - не риманова, но на римановом пространстве-времени лагранжиан (функция  обобщённых координат и описывающая эволюцию системы) сводится к лагранжиану ОТО. Эффекты неметричности в данной теории являются настолько малыми, что ими можно пренебречь даже в нейтронных звёздах. Единственной областью сильных расхождений оказывается, возможно, очень ранняя вселенная. Привлекательной чертой этой теории (и её модификаций) является возможность получения несингулярных решений типа «отскока» для большого взрыва.

---

Теория Эйнштейна-Картана устраняет общерелятивистские проблемы нефизической особенности в большом взрыве . Получаемые поправки к ОТО в условиях современной вселенной настолько малы, что пока не видно даже гипотетических путей для их измерения.

4. 
   Релятивистская теория
   

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А.А. с группой сотрудников. В своих работах они доказывают следующие отличия их теории от ОТО:

• 
  гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.
  

• 
  гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.
  

• 
  В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.
  

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

5. 
   Теория Бранса — Дикке
   

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум группам уравнений для компонента гравитационного поля: одна для метрики, вторая — для скалярного поля. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.

---

Подобное распадение уравнений на два класса имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского. Благодаря наличию безразмерного параметра в теории Йордана — Бранса — Дикке появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов. При этом при стремлении параметра к бесконечности предсказания теории становятся всё более близкими к ОТО, так что опровергнуть теорию Йордана — Бранса — Дикке невозможно никаким экспериментом, подтверждающим общую теорию относительности. Лагранжиан, содержащий полное описание теории Бранса — Дикке, выглядит следующим образом:



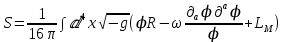
где

• 
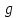  — детерминант метрики,
  
• 
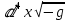  — четырёхмерная форма объёма,
  
• 
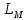  — лагранжиан вещества
  

Для сравнения, в общей теории относительности лагранжиан имеет вид:



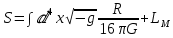
Считая вариации гравитационного члена относительно 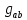, получаем полевые уравнения Эйнштейна в вакууме.
Глава 2. Космические скорости
Гравитационное поле создает вокруг себя любой объект, и у Земли, обладающей внушительной массой, это поле довольно сильно. Именно поэтому строятся мощные многоступенчатые космические ракеты, способные разгонять космические корабли до больших скоростей, которые нужны для преодоления гравитации планеты. Значение этих скоростей и получили названия первая и вторая космические скорости.

1. 
   Первая космическая скорость
   

Понятие первой космической скорости очень простое – это скорость, которую необходимо придать физическому объекту, чтобы он, двигаясь параллельно космическому телу, не смог на него упасть, но в то же время оставался бы на постоянной орбите.

Формула нахождения первой космической скорости не отличается сложностью:

---

Смотрите также файлы

• Занятие 1 Определение организационноправовых форм и видов коммерческих и некоммерческих организаций Цель работы.docx

• Контрольные задания по английскому языку.docx

• Вы работаете в крупной, динамично развивающейся компании менеджером по персоналу. Компания существует более двух лет.docx

• азастан Республикасыны Білім жне ылым Министрлігі Ы. Алтынсарин атындаы лтты білім беру Академиясы лемдік педагогикалы ой сана.doc

• Трбие сааты ыса мерзімді жоспары.docx