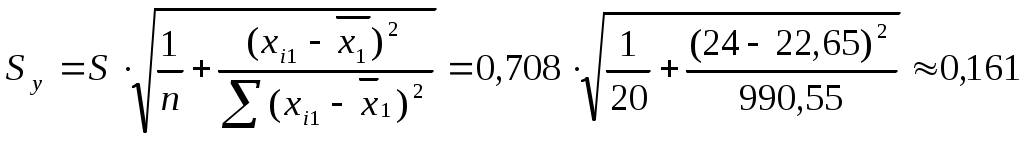Ситуационная (практическая) задача № 1
По 20 предприятиям региона изучается зависимость выработки продукции на

одного работника y (тыс. руб.) от удельного веса рабочих высокой

квалификации в общей численности рабочих x1 (% от стоимости фондов на

конец года) и от ввода в действие новых основных фондов x2 (%).

Требуется:

Требуется:

1. Построить корреляционное поле между выработкой продукции на одного

работника и удельным весом рабочих высокой квалификации. Выдвинуть

гипотезу о тесноте и виде зависимости между показателями X1 и Y.

2. Оценить тесноту линейной связи между выработкой продукции на одного

работника и удельным весом рабочих высокой квалификации с надежностью

0,9.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости

выработки продукции на одного работника от удельного веса рабочих высокой

квалификации.

4. Проверить статистическую значимость параметров уравнения регрессии с

надежностью 0,9 и построить для них доверительные интервалы.

5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера

оценить статистическую значимость уравнения регрессии с надежностью 0,9.

6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки

продукции на одного работника для предприятия, на котором высокую

квалификацию имеют 24% рабочих.

7. Рассчитать коэффициенты линейного уравнения множественной регрессии и

пояснить экономический смысл его параметров.

8. Проанализировать статистическую значимость коэффициентов

множественного уравнения с надежностью 0,9 и построить для них

доверительные интервалы.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации.

Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11. С помощью F -критерия Фишера оценить адекватность уравнения

регрессии с надежностью 0,9.

12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки

продукции на одного работника для предприятия, на котором высокую

квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов

составляет 5%.

13. Проверить построенное уравнение на наличие мультиколлинеарности по:

критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

---

Решение
1. Построить корреляционное поле между выработкой продукции на одного

работника и удельным весом рабочих высокой квалификации. Выдвинуть

гипотезу о тесноте и виде зависимости между показателями X1 и Y.
Построим поле рассеяния:



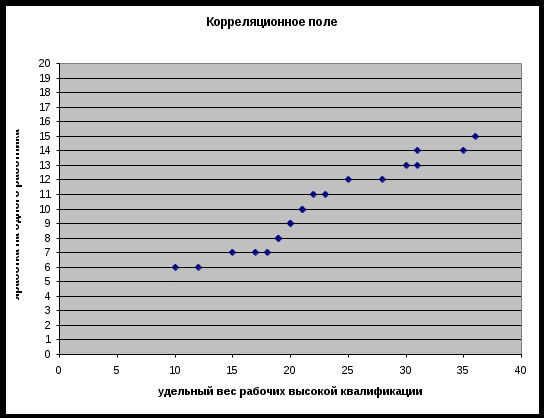
Рис. 1. Корреляционное поле между валовым доходом и стоимостью основных фондов
На основе визуального анализа построенных полей рассеяния можно выдвинуть гипотезу о линейной зависимости валового дохода от стоимости основных фондов.

Математически данная зависимость запишутся в виде:

y = α₀+ α₁x₁ +

- случайная переменная.
2. Оценить тесноту линейной связи между выработкой продукции на одного

работника и удельным весом рабочих высокой квалификации с надежностью

0,9


Составим расчетную таблицу:

Табл.1

i	yi	xi1	xi12	yi xi1	yi2
1	6	10	100	60	36
2	6	12	144	72	36
3	7	15	225	105	49
4	7	17	289	119	49
5	7	18	324	126	49
6	8	19	361	152	64
7	8	19	361	152	64
8	9	20	400	180	81
9	9	20	400	180	81
10	10	21	441	210	100
11	10	21	441	210	100
12	11	22	484	242	121
13	11	23	529	253	121
14	12	25	625	300	144
15	12	28	784	336	144
16	13	30	900	390	169
17	13	31	961	403	169
18	14	31	961	434	196
19	14	35	1225	490	196
20	15	36	1296	540	225
Σ	202	453	11251	4954	2194
среднее	10,1	22,65	562,55	247,7	109,7

---

Найдем коэффициент парной корреляции для :



проверим, существенно ли отличается найденный коэффициент корреляции от нуля. Найдем:



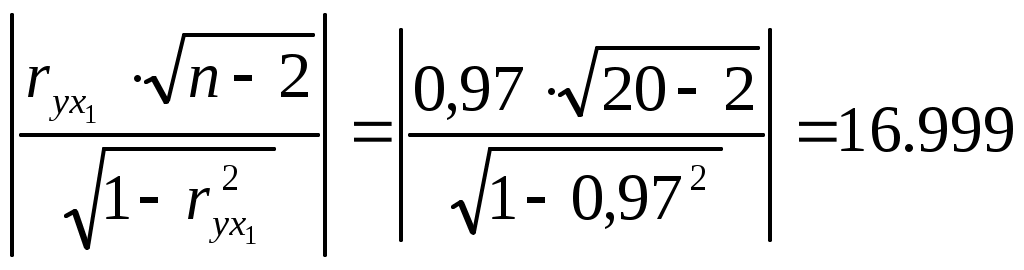
Сравним с квантилем распределения Стьюдента

Т.к. 16,999>1,7341, то коэффициент корреляции существенно отличается от нуля и существует сильная линейная зависимость между y и
3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости

выработки продукции на одного работника от удельного веса рабочих высокой

квалификации.

Методом наименьших квадратов найти оценки линейных уравнений регрессии:






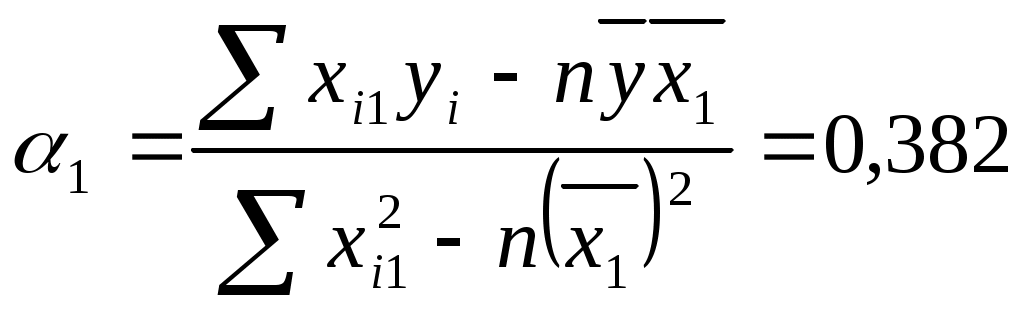
таким образом, получаем уравнение регрессии:


4. Проверить статистическую значимость параметров уравнения регрессии с

надежностью 0,9 и построить для них доверительные интервалы.

Коэффициент детерминации: , т.е. вариация валового дохода на 94,1% объясняется вариацией стоимости основных фондов.

Фактическое значение F-статистики Фишера



Для оценки статистической значимости коэффициентов регрессии найдем , признается статистическая значимость коэффициентов регрессии.

Найдем доверительную полосу для уравнения регрессии , построим вспомогательную таблицу: (таблица 2)

---

Табл.2

ỹi	ỹi -yi	(ỹi -yi )2	(xi1-x1)2	Sy	1,7341Sy	ỹн	ỹв
5,268	-0,732	0,535824	160,0225	0,325559	0,564552	4,703448	5,832552
6,032	0,032	0,001024	113,4225	0,287087	0,497837	5,534163	6,529837
7,178	0,178	0,031684	58,5225	0,233775	0,405389	6,772611	7,583389
7,942	0,942	0,887364	31,9225	0,20297	0,35197	7,59003	8,29397
8,324	1,324	1,752976	21,6225	0,189703	0,328963	7,995037	8,652963
8,706	0,706	0,498436	13,3225	0,178295	0,309181	8,396819	9,015181
8,706	0,706	0,498436	13,3225	0,178295	0,309181	8,396819	9,015181
9,088	0,088	0,007744	7,0225	0,169123	0,293276	8,794724	9,381276
9,088	0,088	0,007744	7,0225	0,169123	0,293276	8,794724	9,381276
9,47	-0,53	0,2809	2,7225	0,162566	0,281905	9,188095	9,751905
9,47	-0,53	0,2809	2,7225	0,162566	0,281905	9,188095	9,751905
9,852	-1,148	1,317904	0,4225	0,158948	0,275631	9,576369	10,12763
10,234	-0,766	0,586756	0,1225	0,158469	0,274802	9,959198	10,5088
10,998	-1,002	1,004004	5,5225	0,166865	0,28936	10,70864	11,28736
12,144	0,144	0,020736	28,6225	0,198816	0,344766	11,79923	12,48877
12,908	-0,092	0,008464	54,0225	0,228855	0,396858	12,51114	13,30486
13,29	0,29	0,0841	69,7225	0,245593	0,425882	12,86412	13,71588
13,29	-0,71	0,5041	69,7225	0,245593	0,425882	12,86412	13,71588
14,818	0,818	0,669124	152,5225	0,31968	0,554357	14,26364	15,37236
15,2	0,2	0,04	178,2225	0,339403	0,588558	14,61144	15,78856
Σ		9,01822	990,55

---

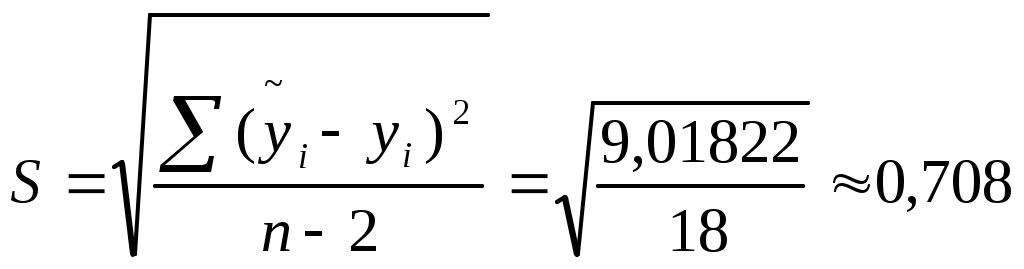, для каждого x_i1 рассчитаем
,

, где . Результаты расчетов для каждого приведены в таблице 2.

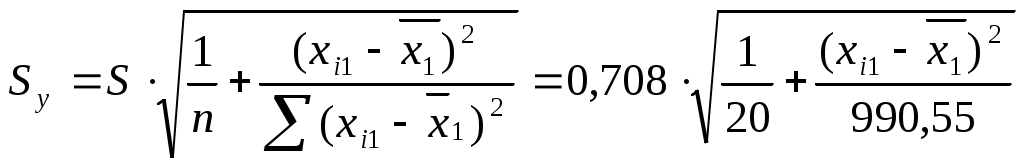Значения определяют доверительный интервал для каждого . Линию регрессии и доверительную полосу изобразим на рисунке 2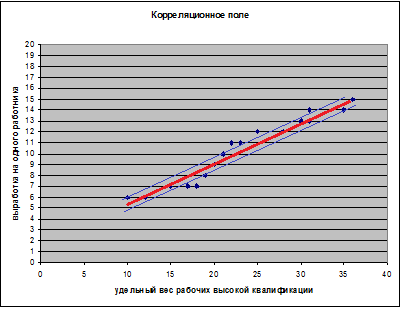



Рис. 2. Линия регрессии и доверительная полоса
5.Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.

Коэффициент детерминации и фактическое значение F -критерия рассчитаны в п.4

При уровне значимости 0,1 табличное значение .

Т.к. 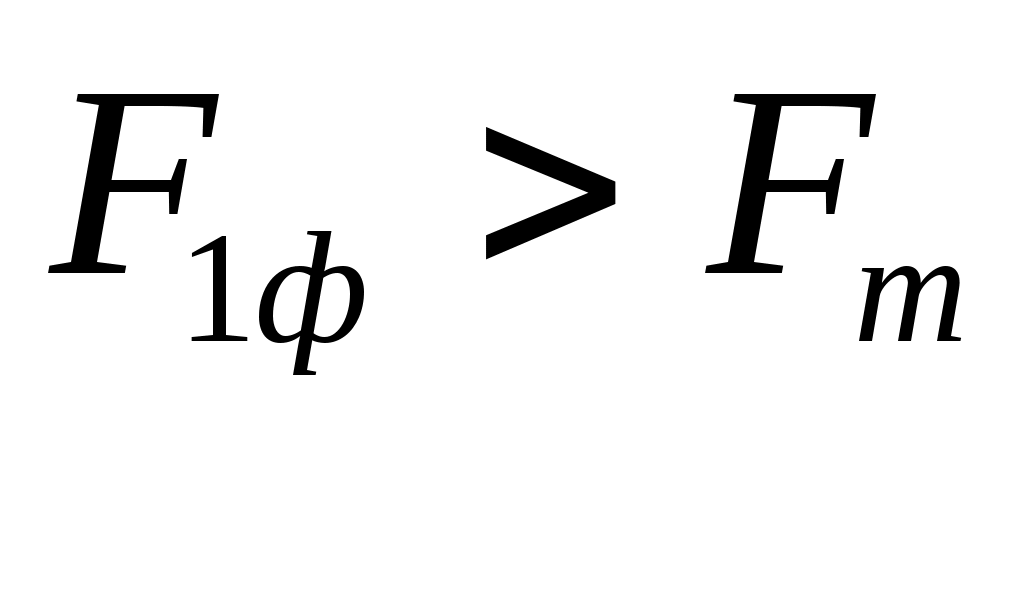, то признается статистическая значимость уравнения регрессии.

6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих.

Точечный прогноз:

Интервальный: 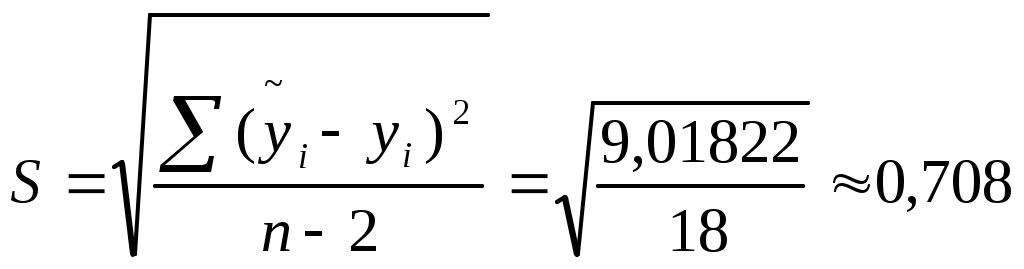, для каждого x_i1 рассчитаем


, где



, т.е., получили доверительный интервал (10,337 ; 10,895).

---

Смотрите также файлы

• Подобные фигуры и их свойства. Признаки подобия треугольников.docx

• Ввод остатков на начало периода.docx

• Составление трёхбуквенных слов, состоящих из изученных букв.docx

• Задача Возле дома посадили 2 вишни и 3 березы. Сколько деревьев стало расти возле дома.docx

• Вербальное общение бывает трех типов.docx