Файл: Задача 1 По 20 предприятиям региона изучается зависимость выработки продукции на.doc
Добавлен: 16.03.2024
Просмотров: 150
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
тенденцию. Проверка значимости коэффициента автокорреляции дает следующий результат:
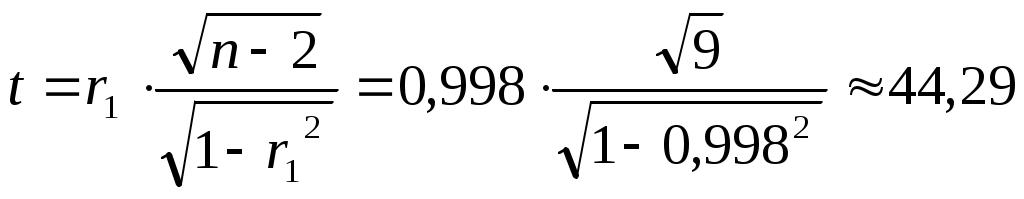
По таблице распределения Стьюдента (двусторонняя критическая область) с уровнем значимости α=0.01 и степенями свободы k=9 находим: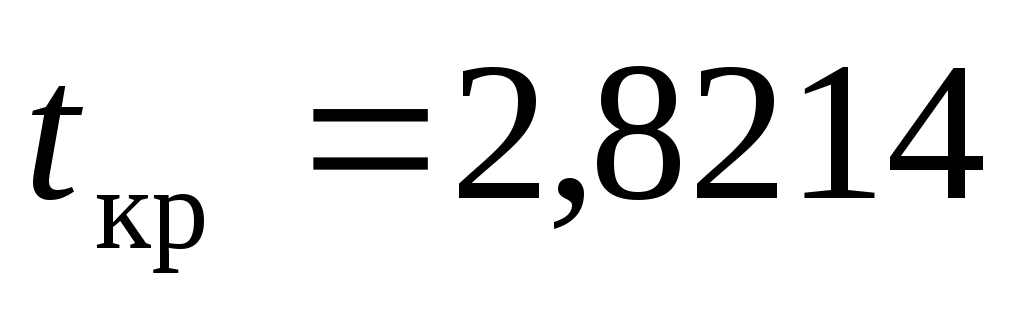
Поскольку tнабл > tкрит, то принимаем гипотезу о значимости коэффициента автокорреляции, что, в свою очередь, подтверждает наличие сильной линейной тенденции. Другими словами, коэффициент автокорреляции статистически значим, сезонная составляющая отсутствует.
Рассчитаем трендовую компоненту ряда динамики.
Т.к. исследование показало наличие линейной связи, опишем его уравнением прямой:
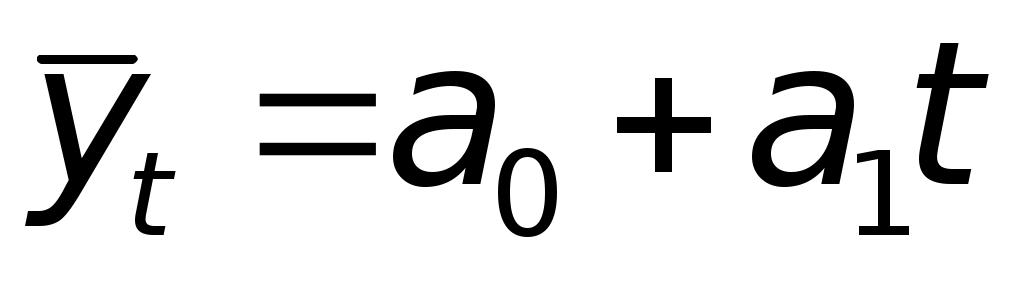
где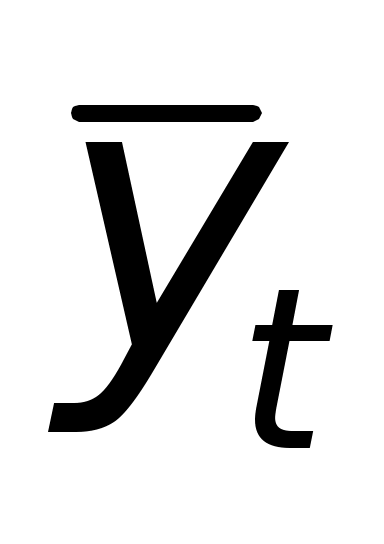
- выровненные значения ряда;
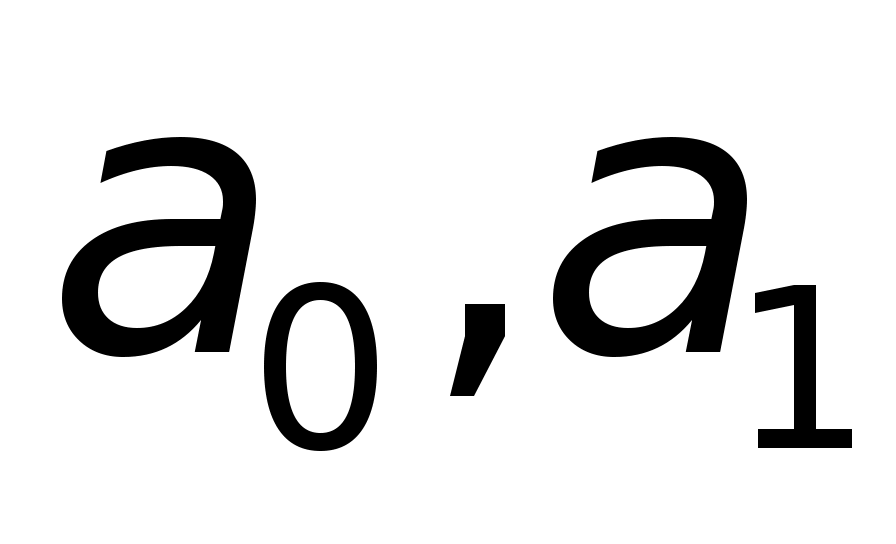- параметры уравнения тренда.
Упрощенный расчет параметров уравнения заключается в переносе начала координат в середину ряда динамики. Тогда система нормальных уравнений для расчета параметров уравнения тренда имеет вид:
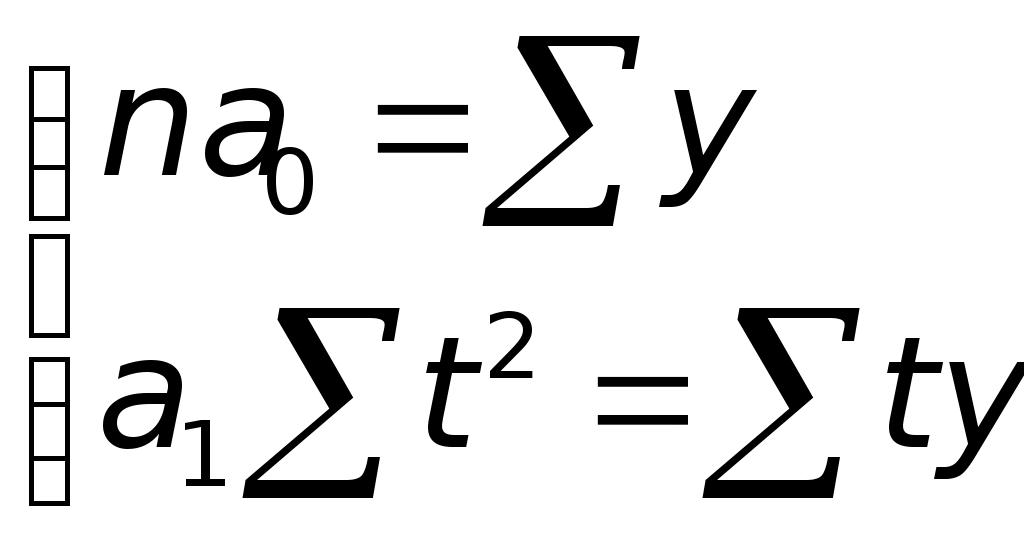
Необходимые промежуточные расчеты приведены в таблице 3.
Таблица 3.
Расчетная таблица для нахождения параметров уравнения тренда
Таким образом, получаем:
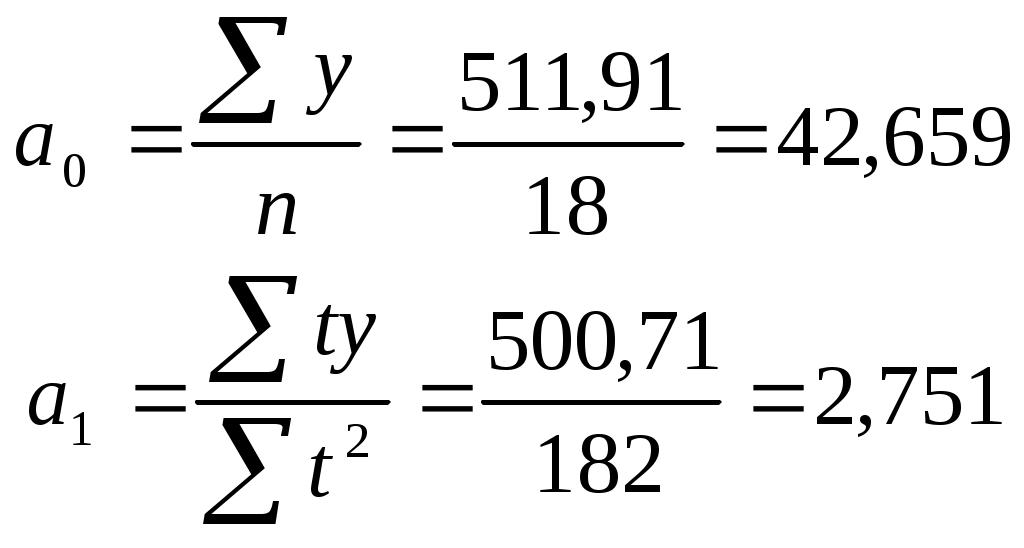
Уравнение тренда имеет вид:
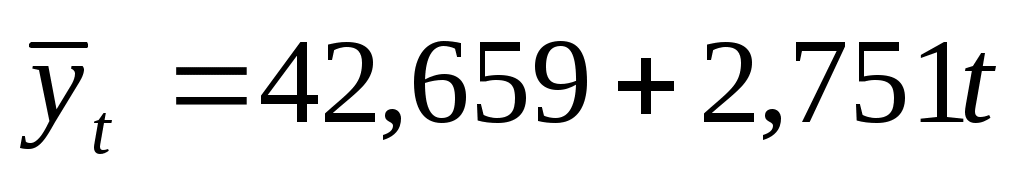
Коэффициент детерминации: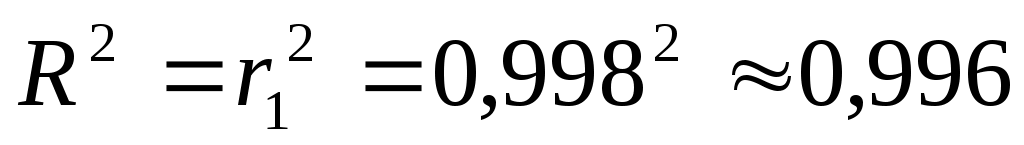
.
Фактическое значение F-статистики Фишера
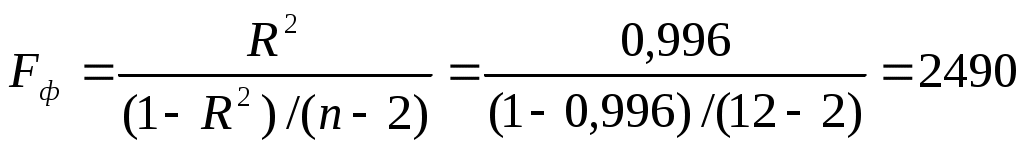
При уровне значимости 0,01 табличное значение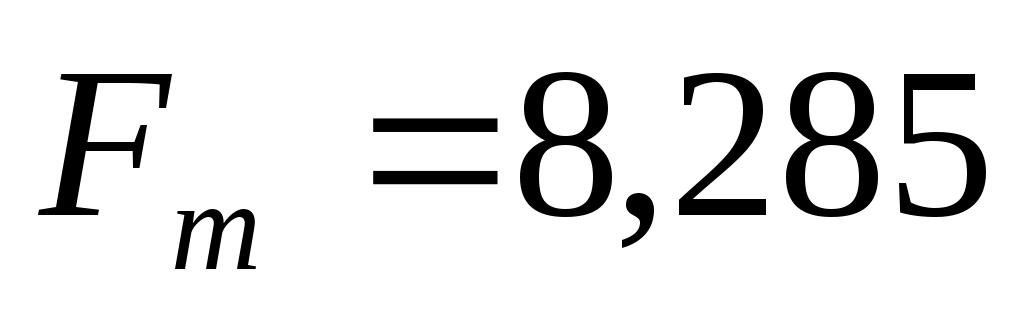
.
Т.к.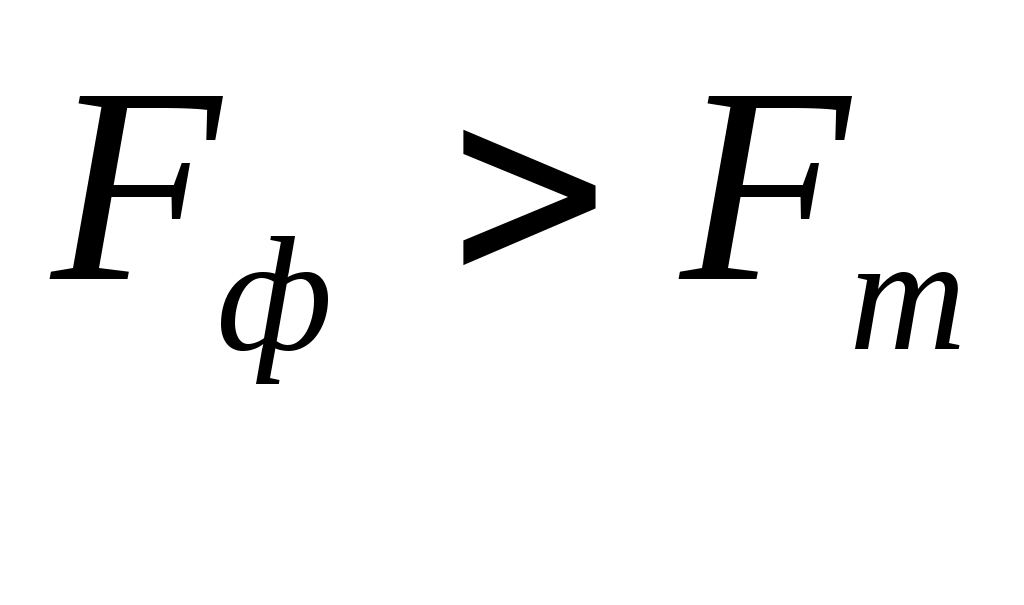
, то признается статистическая значимость уравнения регрессии.
Расчетные (выровненные) значения временного ряда по уравнению тренда приведены в табл. 4.
Прогнозное значение объема платных услуг на 2011 г (t=7):
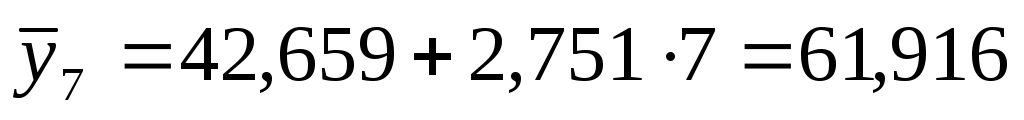ед.
Таким образом, объем платных услуг на 2011 г составляет 61,916 ед.
Интервальный прогноз:
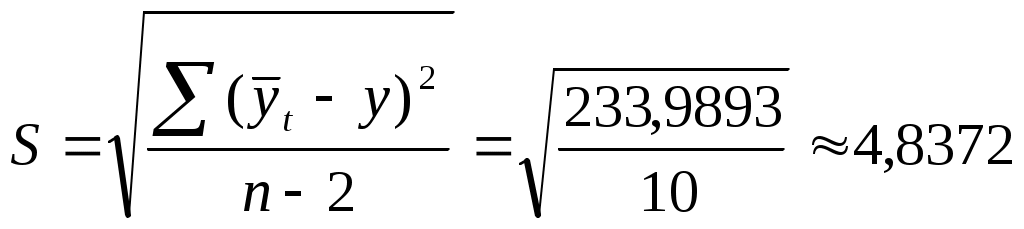, рассчитаем
,
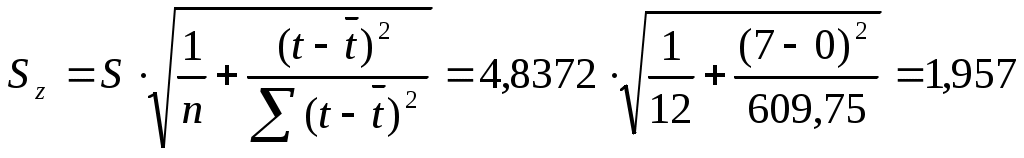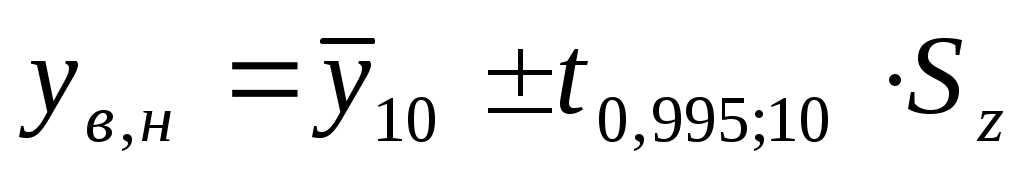, где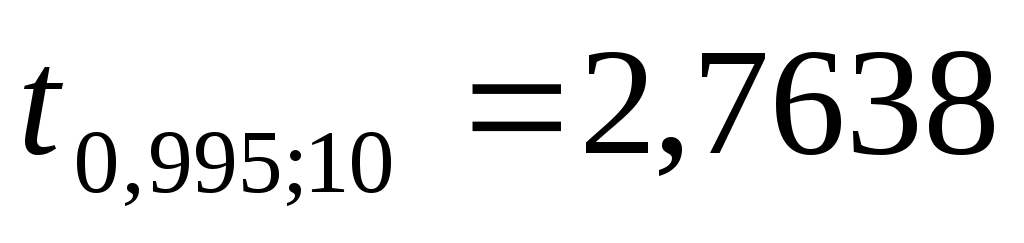 
. Т.е.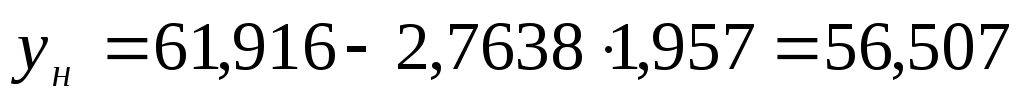 
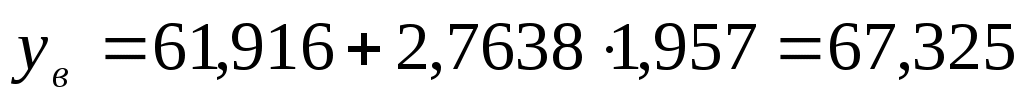
Т.е. с надежностью 99% объем платных услуг в 2011 г . составит (56,507; 67,325) единиц
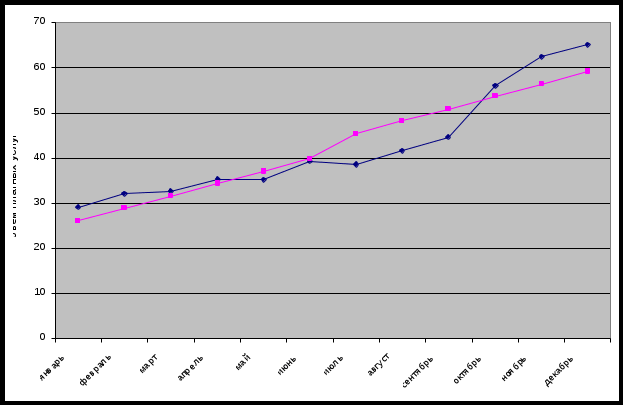
Рис. 2. Исходные данные и линия тренда
Тестовые задания
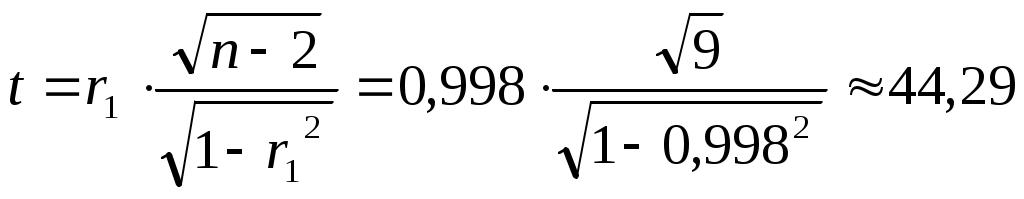
По таблице распределения Стьюдента (двусторонняя критическая область) с уровнем значимости α=0.01 и степенями свободы k=9 находим:
Поскольку tнабл > tкрит, то принимаем гипотезу о значимости коэффициента автокорреляции, что, в свою очередь, подтверждает наличие сильной линейной тенденции. Другими словами, коэффициент автокорреляции статистически значим, сезонная составляющая отсутствует.Рассчитаем трендовую компоненту ряда динамики.
Т.к. исследование показало наличие линейной связи, опишем его уравнением прямой:
где
- выровненные значения ряда; - параметры уравнения тренда.Упрощенный расчет параметров уравнения заключается в переносе начала координат в середину ряда динамики. Тогда система нормальных уравнений для расчета параметров уравнения тренда имеет вид:
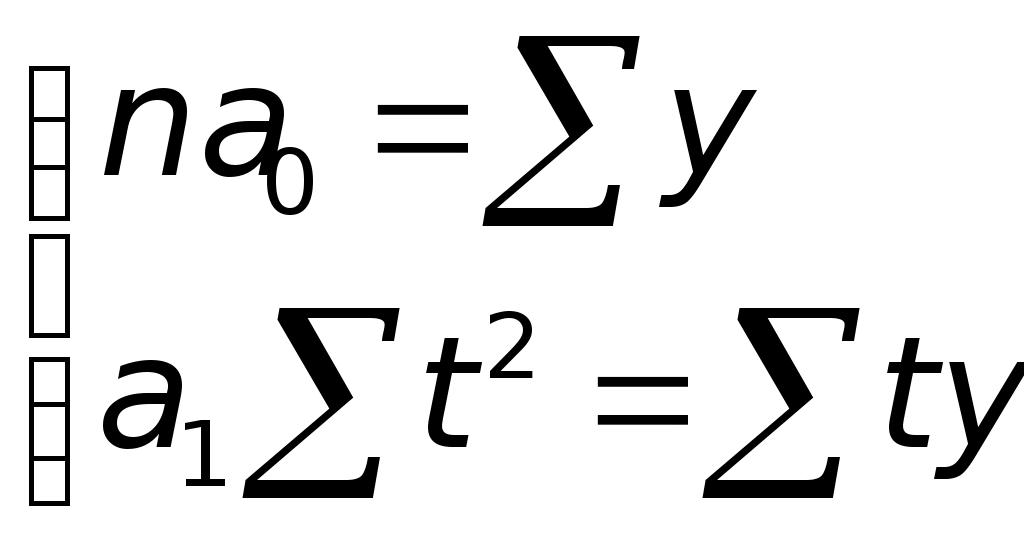
Необходимые промежуточные расчеты приведены в таблице 3.
Таблица 3.
Расчетная таблица для нахождения параметров уравнения тренда
| Месяц, t | Объем платных услуг, у | t |  |  | |
| 1 | 29,08 | -6 | 36 | -174,48 | 26,153 |
| 2 | 32,13 | -5 | 25 | -160,65 | 28,904 |
| 3 | 32,65 | -4 | 16 | -130,6 | 31,655 |
| 4 | 35,43 | -3 | 9 | -106,29 | 34,406 |
| 5 | 35,1 | -2 | 4 | -70,2 | 37,157 |
| 6 | 39,31 | -1 | 1 | -39,31 | 39,908 |
| 7 | 38,53 | 1 | 1 | 38,53 | 45,41 |
| 8 | 41,57 | 2 | 4 | 83,14 | 48,161 |
| 9 | 44,56 | 3 | 9 | 133,68 | 50,912 |
| 10 | 55,98 | 4 | 16 | 223,92 | 53,663 |
| 11 | 62,45 | 5 | 25 | 312,25 | 56,414 |
| 12 | 65,12 | 6 | 36 | 390,72 | 59,165 |
| сумма | 511,91 | 0 | 182 | 500,71 | |
Таким образом, получаем:
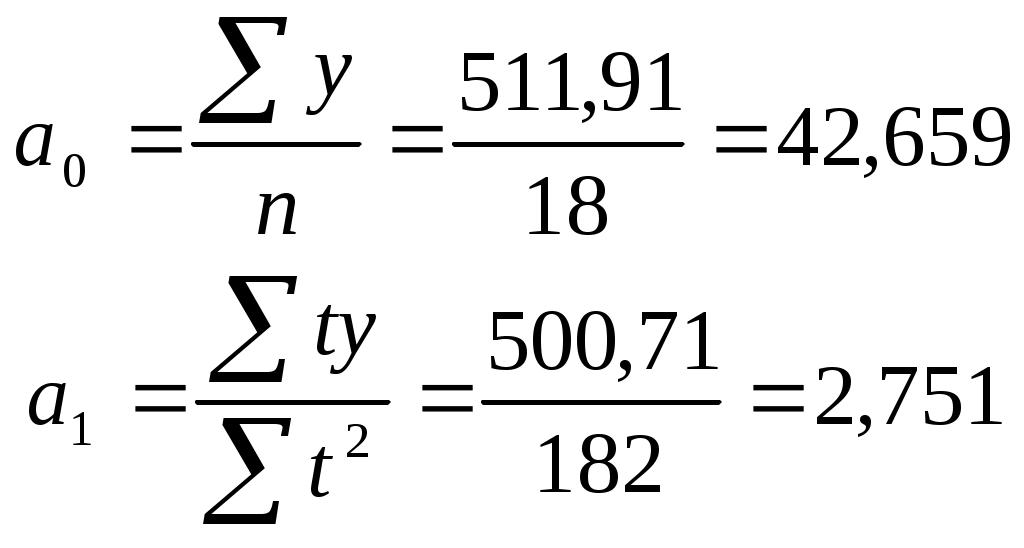
Уравнение тренда имеет вид:
Коэффициент детерминации:
.Фактическое значение F-статистики Фишера
При уровне значимости 0,01 табличное значение
.Т.к.
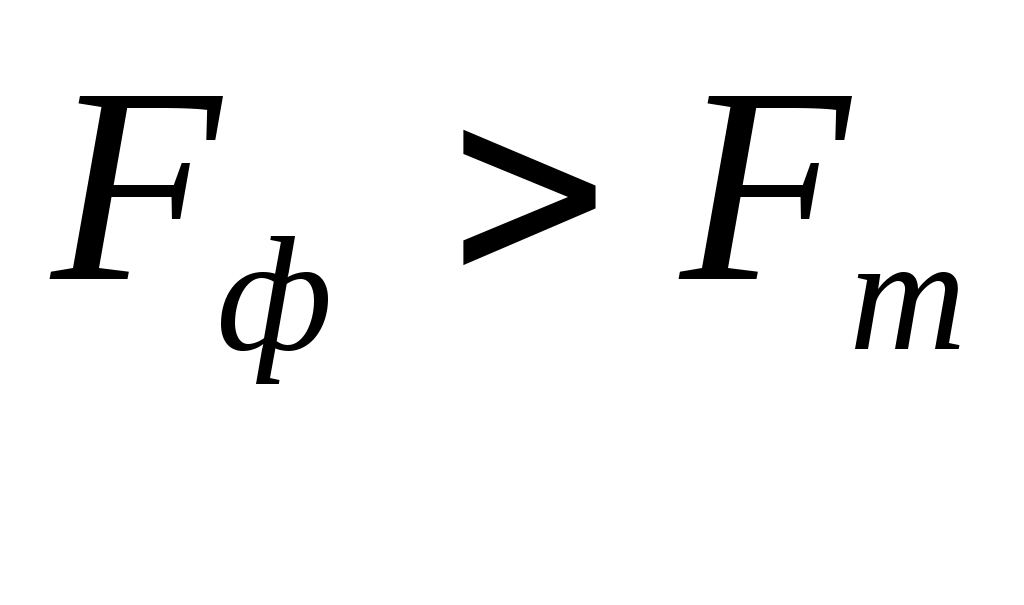, то признается статистическая значимость уравнения регрессии.Расчетные (выровненные) значения временного ряда по уравнению тренда приведены в табл. 4.
Прогнозное значение объема платных услуг на 2011 г (t=7):
ед.Таким образом, объем платных услуг на 2011 г составляет 61,916 ед.
Интервальный прогноз:
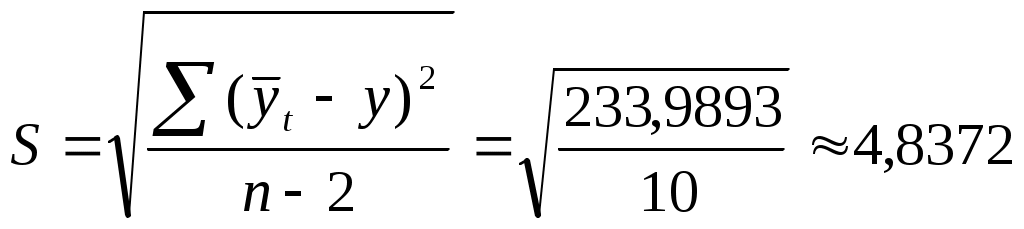, рассчитаем 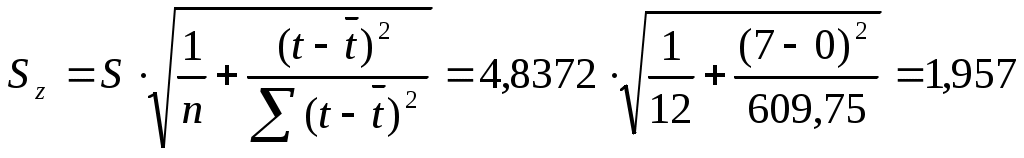, , где . Т.е. Т.е. с надежностью 99% объем платных услуг в 2011 г . составит (56,507; 67,325) единиц
Рис. 2. Исходные данные и линия тренда
Тестовые задания
| Вопрос | Ответ |
| 1 | a) |
| 2 | b) |
| 3 | d) |
| 4 | a) |
| 5 | a) |
| 6 | a) |
| 7 | a) |
| 8 | b) |
| 9 | a) |
| 10 | b) |