Файл: Задача 1 По 20 предприятиям региона изучается зависимость выработки продукции на.doc
Добавлен: 16.03.2024
Просмотров: 148
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.
По методу наименьших квадратов найдем оценки коэффициентов множественной линейной регрессионной модели
Составим матрицы
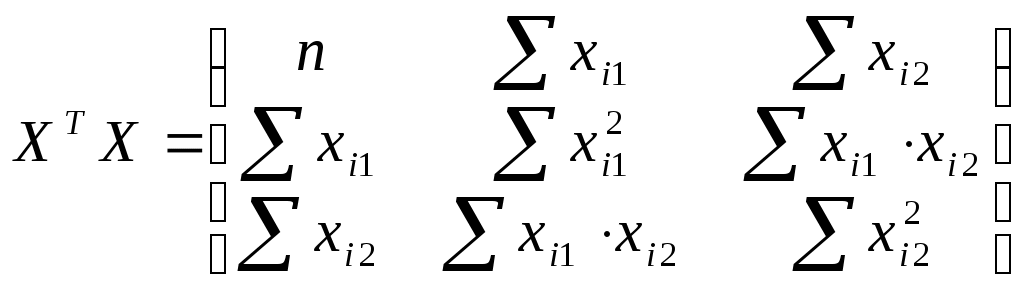 и
и 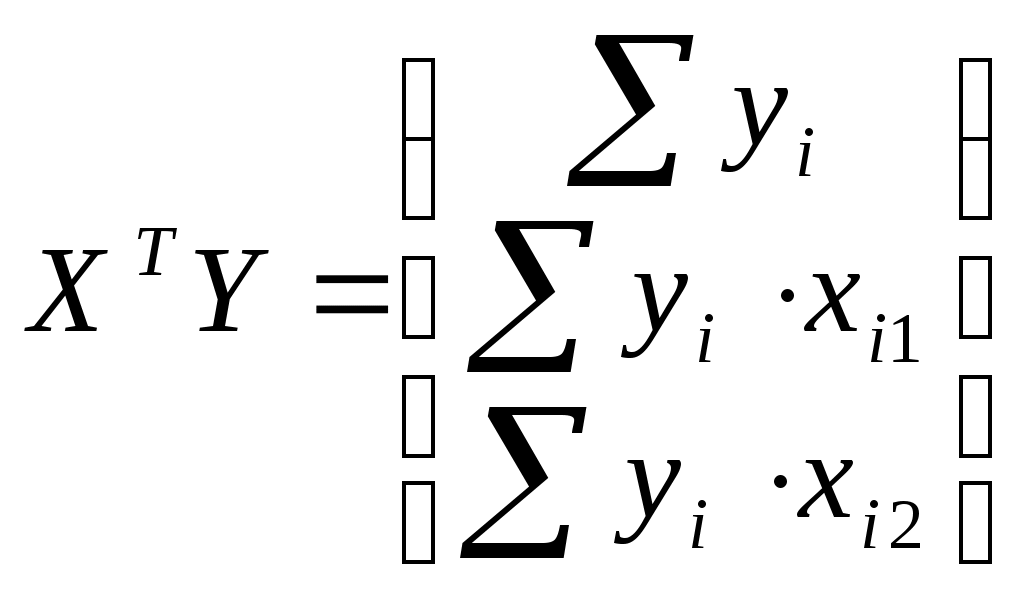
Для этого составим вспомогательную таблицу: (таблица 3)
| i | yi | xi1 | xi2 | xi12 | xi22 | yi xi1 | yi xi2 | xi1xi2 |
| 1 | 6 | 10 | 3,5 | 100 | 12,25 | 60 | 21 | 35 |
| 2 | 6 | 12 | 3,6 | 144 | 12,96 | 72 | 21,6 | 43,2 |
| 3 | 7 | 15 | 3,9 | 225 | 15,21 | 105 | 27,3 | 58,5 |
| 4 | 7 | 17 | 4,1 | 289 | 16,81 | 119 | 28,7 | 69,7 |
| 5 | 7 | 18 | 4,2 | 324 | 17,64 | 126 | 29,4 | 75,6 |
| 6 | 8 | 19 | 4,5 | 361 | 20,25 | 152 | 36 | 85,5 |
| 7 | 8 | 19 | 5,3 | 361 | 28,09 | 152 | 42,4 | 100,7 |
| 8 | 9 | 20 | 5,3 | 400 | 28,09 | 180 | 47,7 | 106 |
| 9 | 9 | 20 | 5,6 | 400 | 31,36 | 180 | 50,4 | 112 |
| 10 | 10 | 21 | 6 | 441 | 36 | 210 | 60 | 126 |
| 11 | 10 | 21 | 6,3 | 441 | 39,69 | 210 | 63 | 132,3 |
| 12 | 11 | 22 | 6,4 | 484 | 40,96 | 242 | 70,4 | 140,8 |
| 13 | 11 | 23 | 7 | 529 | 49 | 253 | 77 | 161 |
| 14 | 12 | 25 | 7,5 | 625 | 56,25 | 300 | 90 | 187,5 |
| 15 | 12 | 28 | 7,9 | 784 | 62,41 | 336 | 94,8 | 221,2 |
| 16 | 13 | 30 | 8,2 | 900 | 67,24 | 390 | 106,6 | 246 |
| 17 | 13 | 31 | 8,4 | 961 | 70,56 | 403 | 109,2 | 260,4 |
| 18 | 14 | 31 | 8,6 | 961 | 73,96 | 434 | 120,4 | 266,6 |
| 19 | 14 | 35 | 9,5 | 1225 | 90,25 | 490 | 133 | 332,5 |
| 20 | 15 | 36 | 10 | 1296 | 100 | 540 | 150 | 360 |
| Σ | 202 | 453 | 125,8 | 11251 | 868,98 | 4954 | 1378,9 | 3120,5 |
| среднее | 10,1 | 22,65 | 6,29 | 562,55 | 43,449 | 247,7 | 68,945 | 156,025 |
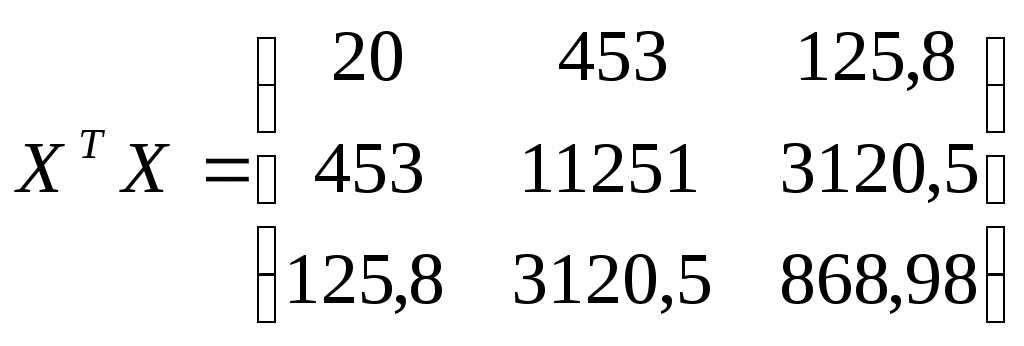 ;
; 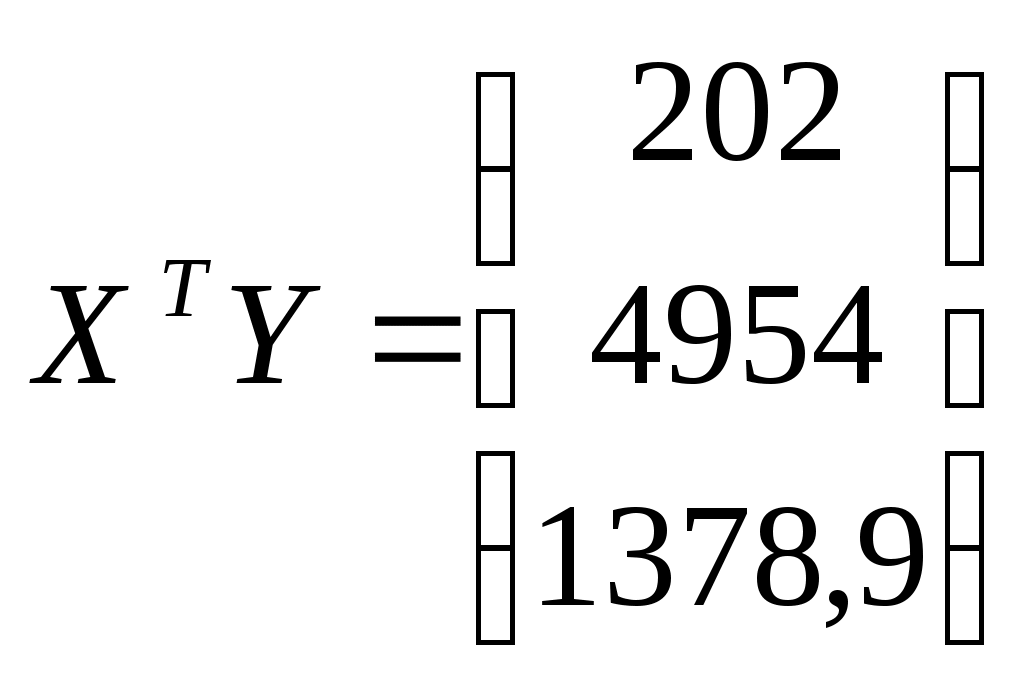
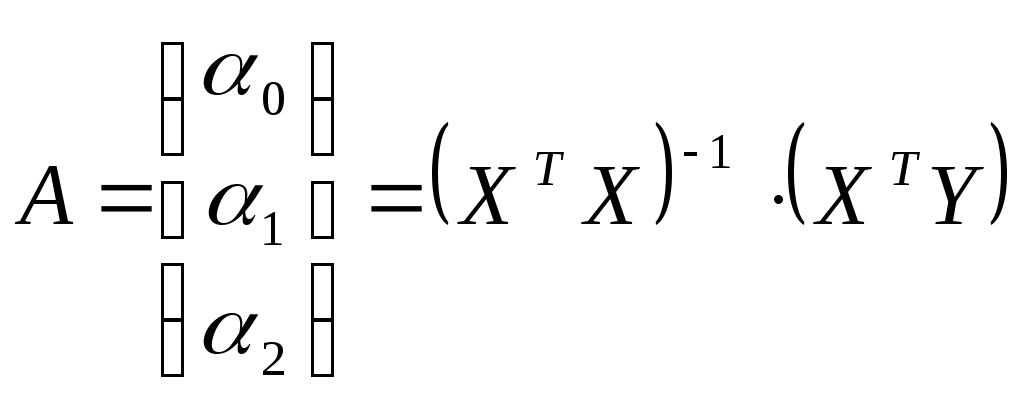
Обратная матрица

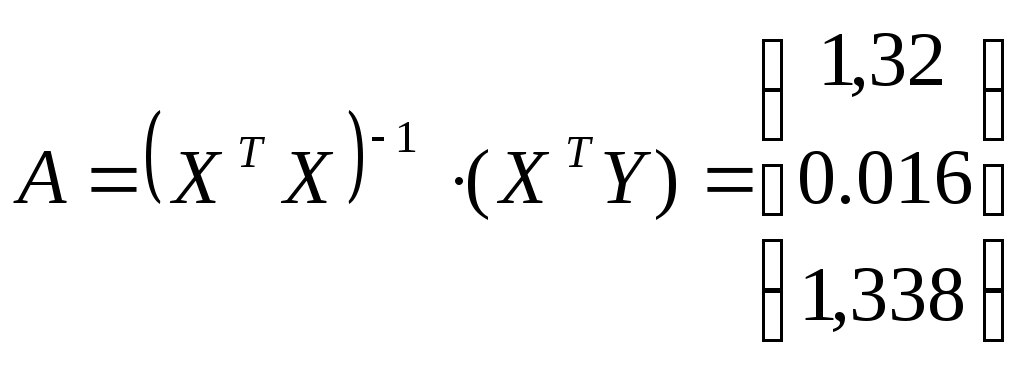 таким образом, получаем уравнение регрессии:
таким образом, получаем уравнение регрессии:Коэффициент
Коэффициент
8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
Для вычисления коэффициента детерминации составим таблицу: (таблица 4)
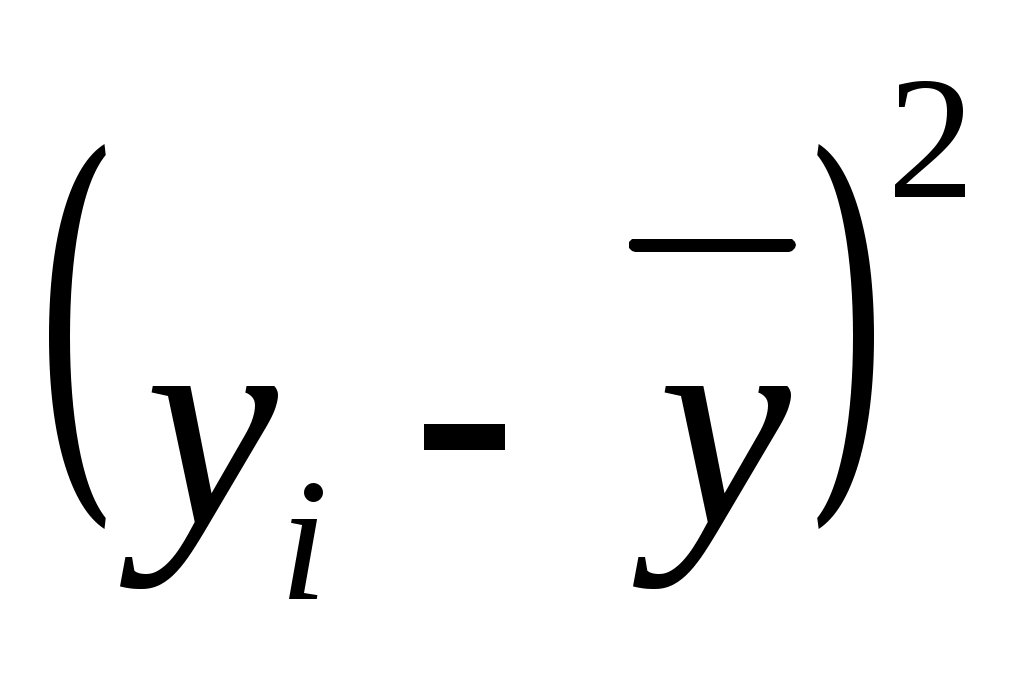
| ỹi | ỹi -yi | (ỹi -yi )2 | |
| 6,163 | 0,163 | 0,026569 | 16,81 |
| 6,3288 | 0,3288 | 0,108109 | 16,81 |
| 6,7782 | -0,2218 | 0,049195 | 9,61 |
| 7,0778 | 0,0778 | 0,006053 | 9,61 |
| 7,2276 | 0,2276 | 0,051802 | 9,61 |
| 7,645 | -0,355 | 0,126025 | 4,41 |
| 8,7154 | 0,7154 | 0,511797 | 4,41 |
| 8,7314 | -0,2686 | 0,072146 | 1,21 |
| 9,1328 | 0,1328 | 0,017636 | 1,21 |
| 9,684 | -0,316 | 0,099856 | 0,01 |
| 10,0854 | 0,0854 | 0,007293 | 0,01 |
| 10,2352 | -0,7648 | 0,584919 | 0,81 |
| 11,054 | 0,054 | 0,002916 | 0,81 |
| 11,755 | -0,245 | 0,060025 | 3,61 |
| 12,3382 | 0,3382 | 0,114379 | 3,61 |
| 12,7716 | -0,2284 | 0,052167 | 8,41 |
| 13,0552 | 0,0552 | 0,003047 | 8,41 |
| 13,3228 | -0,6772 | 0,4586 | 15,21 |
| 14,591 | 0,591 | 0,349281 | 15,21 |
| 15,276 | 0,276 | 0,076176 | 24,01 |
| | | 2,777991 | 153,8 |
Значимость параметров уравнения регрессии оценивается с помощью t-критерия Стьюдента.
Для расчета t-статистик коэффициентов необходимо рассчитать их стандартные ошибки:
где
Получаем:
Тогда t-статистики коэффициентов равны:
При уровне значимости
Т.к.
Интервальная оценка для коэффициента
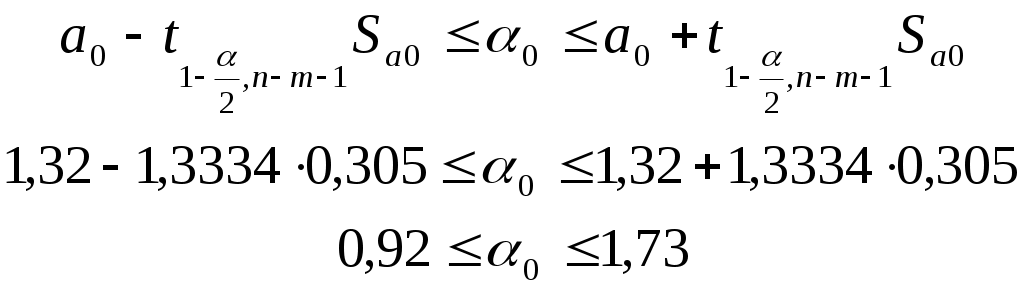
Таким образом, истинное значение
Интервальная оценка для коэффициента
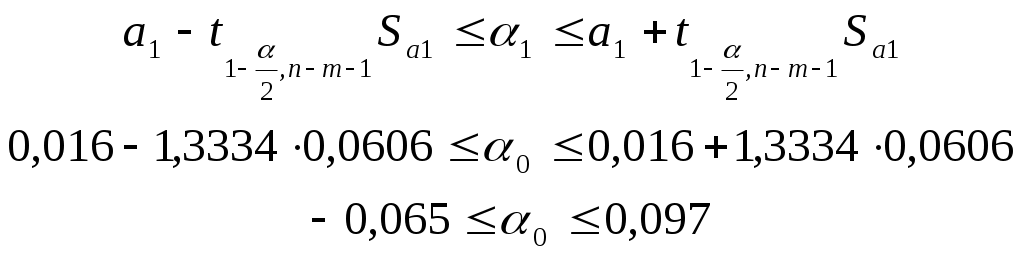
Таким образом, истинное значение
Интервальная оценка для коэффициента
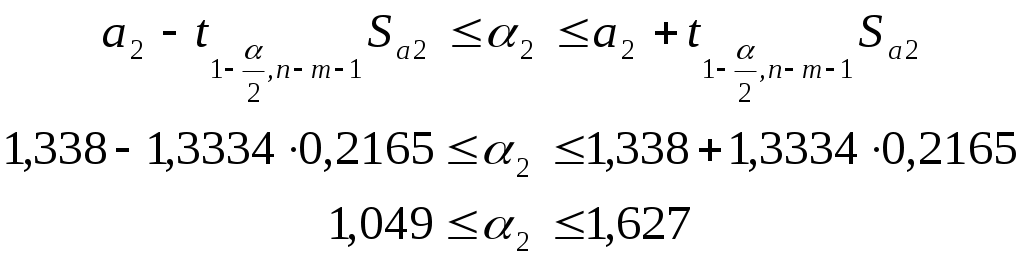
Таким образом, истинное значение
9. Найти коэффициенты парной и частной корреляции. Проанализировать их.
Парные коэффициенты корреляции применяются для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) – результаты промежуточных вычислений – см. табл. 3.
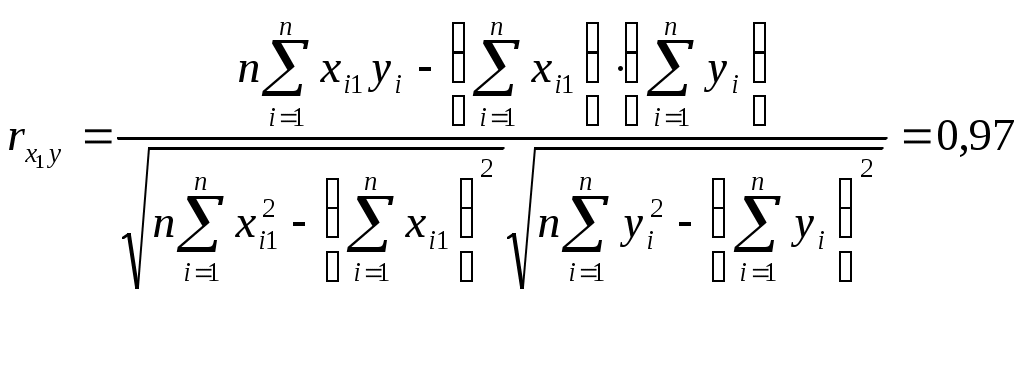
Промежуточные вычисления приведены в таблице 4. В данном случае
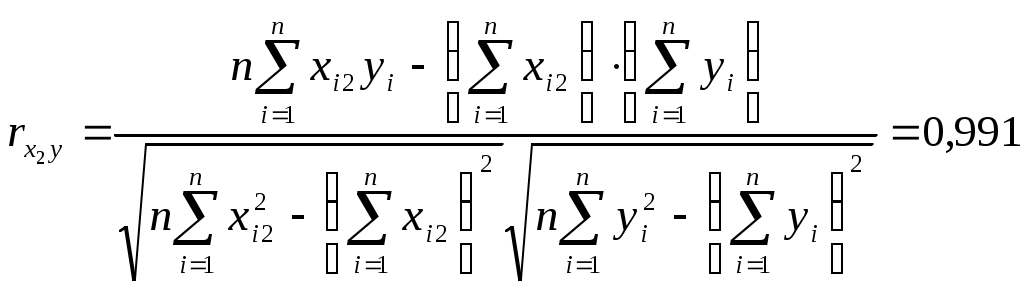
В данном случае
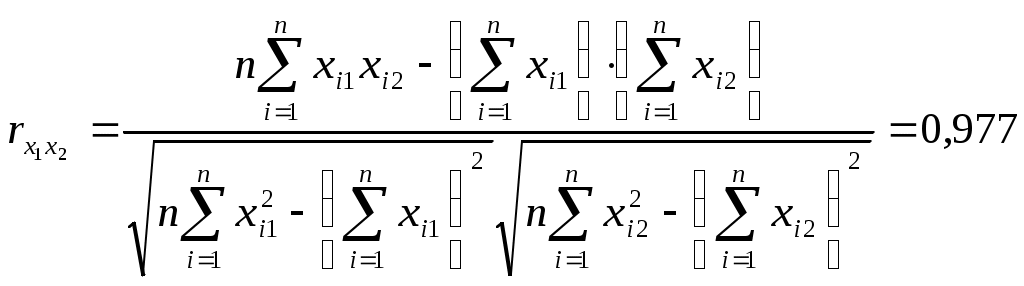
В данном случае
Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели:
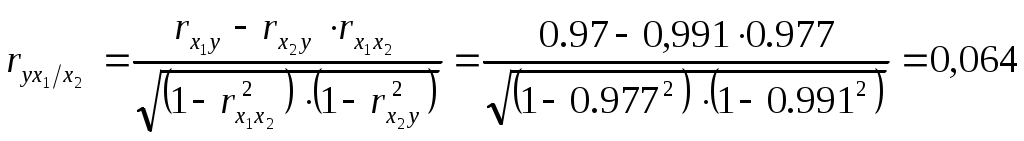
Полученное значение говорит о том, что между выработкой продукции и удельным весом рабочих высокой квалификации при фиксированном значении ввода в действие основных фондов существует слабая прямая зависимость.
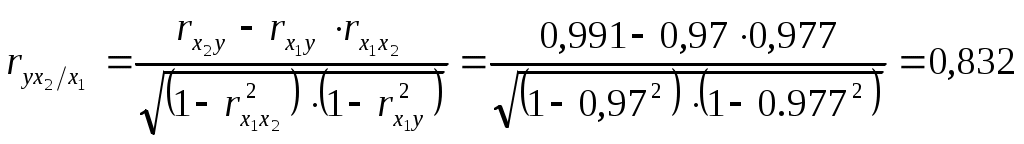
Полученное значение говорит о том, что между выработкой и вводом в действие основных средств при фиксированном значении удельного веса квалифицированных рабочих существует тесная прямая зависимость.
10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
Коэффициент множественной детерминации равен:
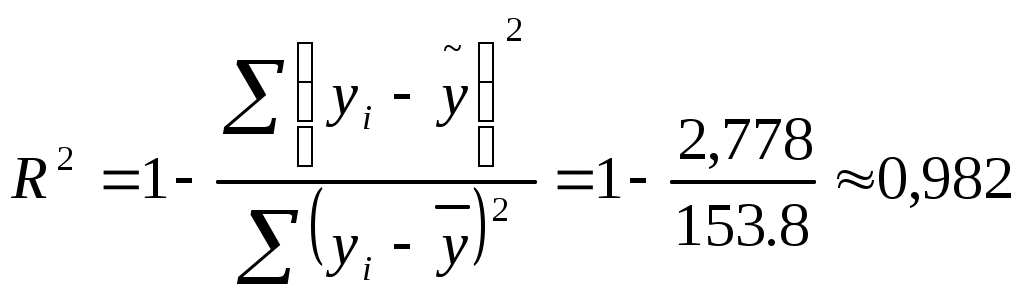
Следовательно, регрессия y на x1 и x 2 объясняет 98,2% колебаний значений у. Это свидетельствует о значительном суммарном влиянии независимых переменных x1 и x 2 на зависимую переменную у.
Для того чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику
где n – количество наблюдений;
m – количество факторных признаков.
Получаем:
Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве факторов). Поэтому теряется интерпретация показателя как «доли». Тем не менее, применение показателя в сравнении вполне обоснованно.
11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.
Качество уравнения также оценивается с помощью F-теста. Расчетное значение F-критерия:
В данном случае
