Критическое значение F-критерия при уровне значимости и степенях свободы составит:



Т.к. , признается статистическая значимость уравнения регрессии.
12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
При , находим точечный прогноз:



тыс.руб.

Интервальный прогноз среднего значения накоплений домохозяйств:



где - соответственно верхняя и нижняя границы доверительного интервала;

- вектор независимых переменных;

- квантиль распределения Стьюдента (табличное значение);

– доверительная вероятность;

– количество степеней свободы.









Тогда ;

Пусть , тогда

---

;





Таким образом, для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5% с вероятностью 90% выработка попадет в интервал от 7,749 до 9,039 тыс. руб.
13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.
Для проверки построенного уравнения множественного уравнения регрессии на мультиколлинеарность необходимо определить коэффициент парной корреляции между объясняющими переменными (расчеты коэффициента см. выше):

, что говорит о слабой обратной зависимости между стоимостью основных фондов и оборотных средств.

Проверка существенности отличия коэффициента корреляции от нуля (значимости) проводится по схеме:

если ,

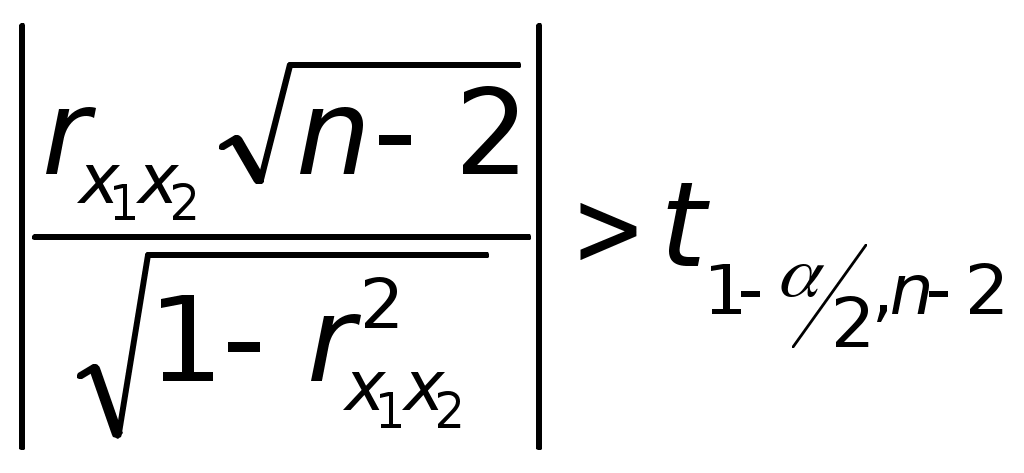то гипотеза о существенном отличии коэффициента корреляции от нуля принимается, в противном случае – отвергается.

Здесь – уровень значимости (уровень доверия);

– количество степеней свободы;

- квантиль распределения Стьюдента (находится по таблицам).



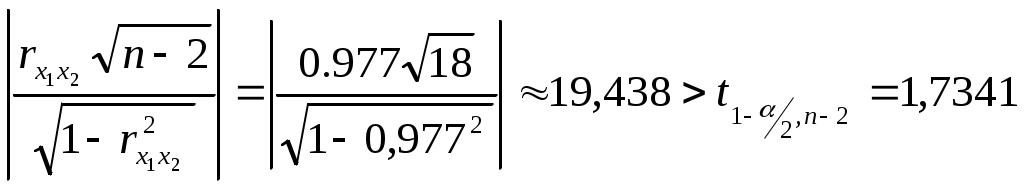
Следовательно, коэффициент корреляции существенно отличается от нуля и существует линейная связь между и . Следовательно, можно сделать вывод о наличии мультиколлинерности между факторными признаками.

Проверим гипотезу о независимости объясняющих переменных с помощью критерия «хи-квадрат»:

Рассчитаем определитель матрицы коэффициентов парной корреляции:

---

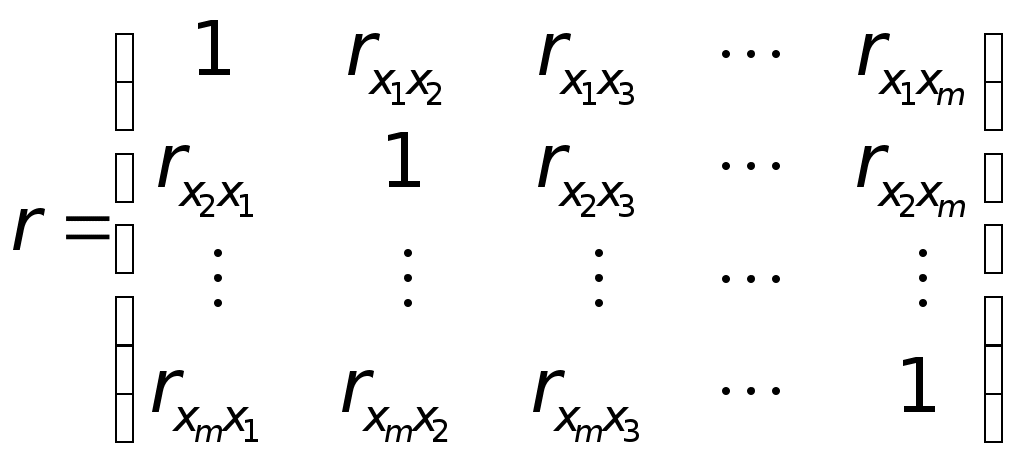
Для данной задачи:



Фактическое значение статистики «хи-квадрат»:



где - количество наблюдений;

- число объясняющих переменных.

Число степеней свободы:



Получаем:



Табличное значение статистики для и равно . В этом случае выполняется неравенство:



Следовательно, можно сделать вывод о наличии мультиколлинеарности.

Ситуационная (практическая) задача №2
Имеются помесячные данные по объему платных услуг населению в 2010 г.
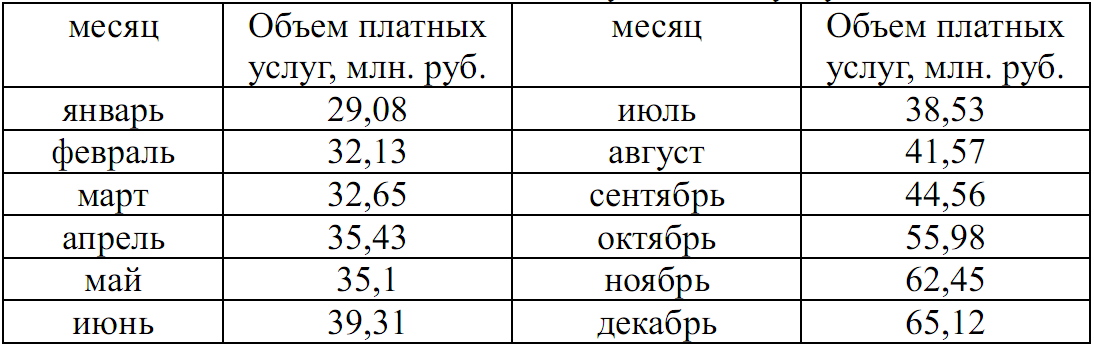
Требуется:

1. Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,99.

4. Дать точечный и интервальный прогноз объема платных услуг на февраль 2011 г. с надежностью 0,99.


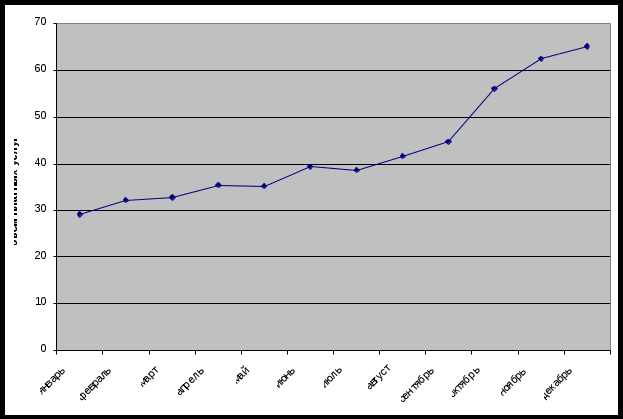
Рис.1

Количественное измерение корреляции осуществляется посредством использования линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени:



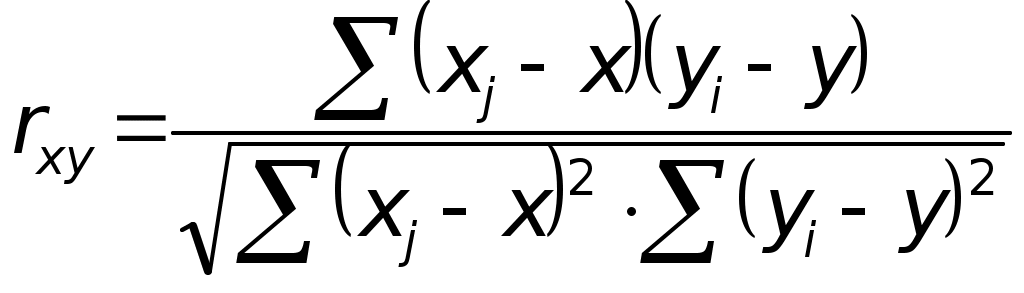
Если сдвиг во времени составляет всего один шаг, то соответствующий коэффициент корреляции называется коэффициентом автокорреляции уровней ряда первого порядка

---

. При этом лаг равен 1. Измеряется же зависимость между соседними уровнями ряда. В общем случае число шагов (или циклов), на которые осуществляется сдвиг, характеризующий влияние запаздывания, также называется лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.
Таблица 2.

Расчетная таблица для определения коэффициента автокорреляции

Месяц, t	Объем платных услуг, у	Выпуск с лагом 1
1	29,08	32,13	934,3404	845,6464	1032,3369
2	32,13	32,65	1049,0445	1032,3369	1066,0225
3	32,65	35,43	1156,7895	1066,0225	1255,2849
4	35,43	35,1	1243,593	1255,2849	1232,01
5	35,1	39,31	1379,781	1232,01	1545,2761
6	39,31	38,53	1514,6143	1545,2761	1484,5609
7	38,53	41,57	1601,6921	1484,5609	1728,0649
8	41,57	44,56	1852,3592	1728,0649	1985,5936
9	44,56	55,98	2494,4688	1985,5936	3133,7604
10	55,98	62,45	3495,951	3133,7604	3900,0025
11	62,45	65,12	4066,744	3900,0025	4240,6144
сумма	446,79	482,83	20789,3778	19208,5591	22603,5271
среднее	40,617	43,894	1889,943	1746,233	2054,866

---

Получаем:



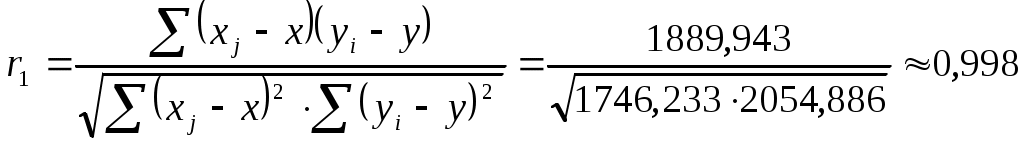
Так как коэффициент автокорреляции первого порядка оказался высоким, то исследуемый ряд содержит только

---

Смотрите также файлы

• Подобные фигуры и их свойства. Признаки подобия треугольников.docx

• Ввод остатков на начало периода.docx

• Составление трёхбуквенных слов, состоящих из изученных букв.docx

• Задача Возле дома посадили 2 вишни и 3 березы. Сколько деревьев стало расти возле дома.docx

• Вербальное общение бывает трех типов.docx