Файл: 1 в треугольнике против угла в 150 лежит большая сторона.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
— радиус описанной окружности.
Для любого треугольника верна теорема синусов:
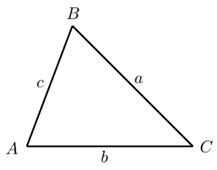
Теорема синусов:
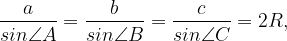
R — радиус описанной окружности
Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.
Решение:
Выразим площадь треугольника двумя разными способами:
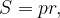
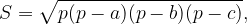 где
где  – полупериметр треугольника, a
– полупериметр треугольника, a 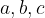 – его стороны.
– его стороны.
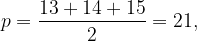
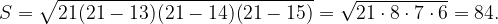
Тогда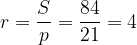 , а диаметр окружности равен
, а диаметр окружности равен 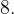
Ответ: 8.
Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен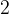 . Найдите гипотенузу c этого треугольника. В ответе укажите
. Найдите гипотенузу c этого треугольника. В ответе укажите 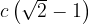 .
.
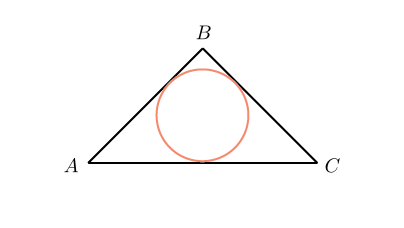
Решение:
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна
. Тогда гипотенуза равна 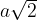 .
.
Запишем площадь треугольника АВС двумя способами:
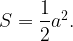
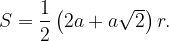
Приравняв эти выражения, получим, что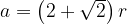 . Поскольку
. Поскольку 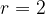 , получаем, что
, получаем, что 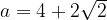 .
.
Тогда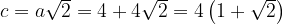 .
.
В ответ запишем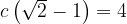 .
.
Ответ: 4.
Задача 4, ЕГЭ. В треугольнике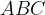 сторона
сторона  равна
равна 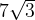 , а угол
, а угол 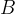 равен
равен 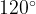 . Найдите радиус описанной около этого треугольника окружности.
. Найдите радиус описанной около этого треугольника окружности.
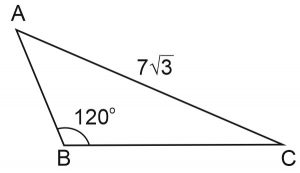
Решение:
По теореме синусов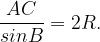
Тогда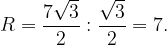
Ответ: 7.
Задача 5, ЕГЭ. В треугольнике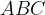 угол А равен
угол А равен 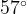 , а угол В –
, а угол В –  . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника 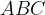
, если сторона равна 10.
равна 10.
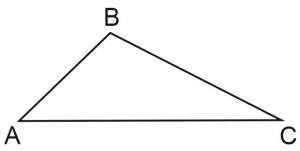
Решение:
Зная, что сумма углов треугольника равна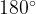 , найдем угол С.
, найдем угол С.
По теореме синусов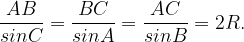
Значит,
Ответ: 10.
Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
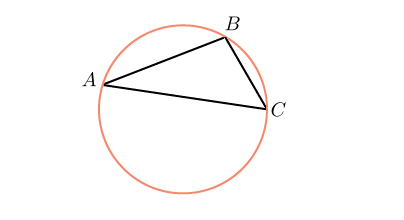
По теореме синусов,

Получаем, что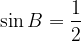 . Угол
. Угол  — тупой. Значит, он равен
— тупой. Значит, он равен 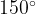 .
.
Ответ: 150.
Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны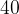 , основание равно
, основание равно 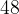 . Найдите радиус описанной окружности этого треугольника.
. Найдите радиус описанной окружности этого треугольника.
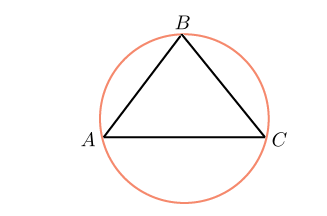
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

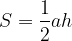 , где
, где 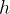 — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону
— высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону
 пополам. По теореме Пифагора найдем
пополам. По теореме Пифагора найдем 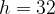 .
.
Тогда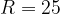 .
.
Ответ: 25.
Задача 8, ОГЭ. В равнобедренном треугольнике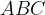 основание
основание 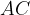 равно 10 см, а высота, проведенная к основанию, 12 см. Найдите периметр треугольника и радиус вписанной окружности.
равно 10 см, а высота, проведенная к основанию, 12 см. Найдите периметр треугольника и радиус вписанной окружности.
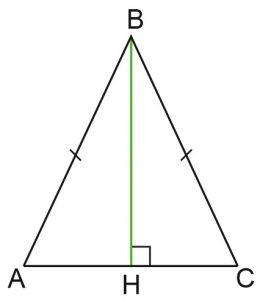
Решение:
Высота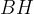 , проведенная к основанию
, проведенная к основанию 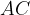 , является медианой. Значит,
, является медианой. Значит, 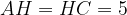 .
.
 находится по теореме Пифагора из треугольника
находится по теореме Пифагора из треугольника 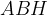 :
:
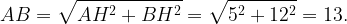
Периметр треугольника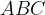 – это сумма длин сторон, т.е.
– это сумма длин сторон, т.е. 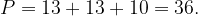
Площадь треугольника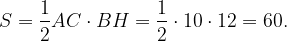
Радиус вписанной окружности r найдем по формуле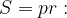
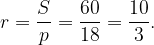
Ответ: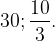
Задача 9, ОГЭ. Стороны и
и 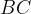 треугольника
треугольника 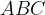 равны 6 и
равны 6 и 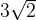 соответственно, угол
соответственно, угол 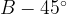 . Найдите диаметр окружности, описанной около треугольника
. Найдите диаметр окружности, описанной около треугольника 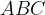 .
.
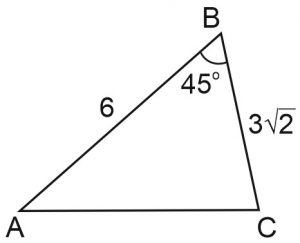
Решение:
Найдем длину стороны по теореме косинусов, используя длины сторон
по теореме косинусов, используя длины сторон  ,
, 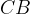 и косинус угла В, противолежащего стороне
и косинус угла В, противолежащего стороне  :
:
Теперь воспользуемся теоремой синусов:
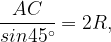
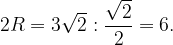
Значит, диаметр окружности, описанной около треугольника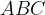 , равен 6.
, равен 6.
Ответ: 6.
Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.
Решение:
Пусть длина радиуса описанной окружности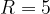 , а длина радиуса вписанной окружности
, а длина радиуса вписанной окружности 
Мы знаем, что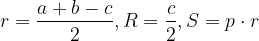
Для любого треугольника верна теорема синусов:

Теорема синусов:
R — радиус описанной окружности
Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.
Решение:
Выразим площадь треугольника двумя разными способами:
Тогда
Ответ: 8.
Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен

Решение:
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что
Тогда
В ответ запишем
Ответ: 4.
Задача 4, ЕГЭ. В треугольнике

Решение:
По теореме синусов
Тогда
Ответ: 7.
Задача 5, ЕГЭ. В треугольнике
, если сторона

Решение:
Зная, что сумма углов треугольника равна
По теореме синусов
Значит,
Ответ: 10.
Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,
Получаем, что
Ответ: 150.
Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
Тогда
Ответ: 25.
Задача 8, ОГЭ. В равнобедренном треугольнике

Решение:
Высота
Периметр треугольника
Площадь треугольника
Радиус вписанной окружности r найдем по формуле
Ответ:
Задача 9, ОГЭ. Стороны

Решение:
Найдем длину стороны
Теперь воспользуемся теоремой синусов:
Значит, диаметр окружности, описанной около треугольника
Ответ: 6.
Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.
Решение:
Пусть длина радиуса описанной окружности
Мы знаем, что

