Файл: 1 в треугольнике против угла в 150 лежит большая сторона.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, где  – полупериметр,
– полупериметр, 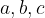 – стороны треугольника.
– стороны треугольника.
Значит,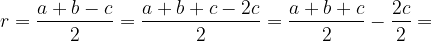
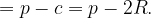
Отсюда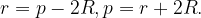
Тогда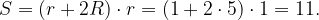
Ответ: 11.
Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.
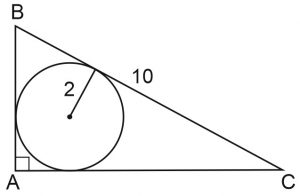
Решение:
Пусть радиус вписанной окружности , а гипотенуза
, а гипотенуза 
Мы знаем, что в прямоугольном треугольнике
Значит,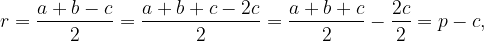 отсюда
отсюда 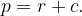
Площадь находится по формуле где
где  – полупериметр,
– полупериметр, 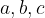 – стороны треугольника.
– стороны треугольника.
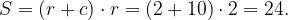
Ответ: 24.
Рассмотрим также задачу из 2 части ЕГЭ по математике.
Задача 12. Точка О – центр вписанной в треугольник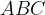 окружности. Прямая
окружности. Прямая 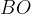
вторично пересекает описанную около треугольника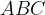 окружность в точке Р.
окружность в точке Р.
а) Докажите, что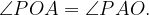
б) Найдите площадь треугольника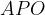 , если радиус окружности, описанной около треугольника
, если радиус окружности, описанной около треугольника 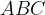 равен 10,
равен 10, 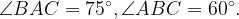
Решение:
а) Пусть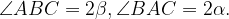 О – центр вписанной окружности, значит,
О – центр вписанной окружности, значит, 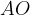 и
и  – биссектрисы углов
– биссектрисы углов 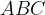 и
и 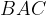 соответственно, и
соответственно, и 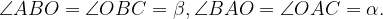
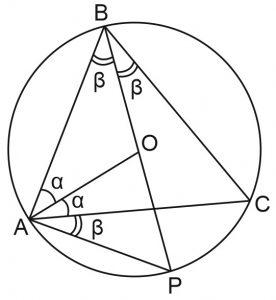
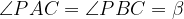 как вписанные углы, опирающиеся на одну и ту же дугу
как вписанные углы, опирающиеся на одну и ту же дугу 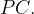
Тогда
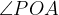 – внешний угол треугольника
– внешний угол треугольника  , поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е.
, поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е. 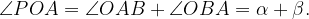
Значит, Что и требовалось доказать.
Что и требовалось доказать.
б)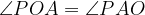 , следовательно, треугольник
, следовательно, треугольник 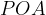 – равнобедренный,
– равнобедренный,  – основание,
– основание, 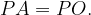
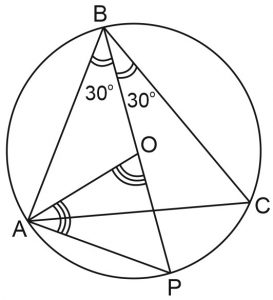
Угол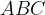 равен
равен 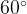 , значит,
, значит, 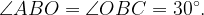
По теореме синусов для треугольника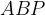 :
:
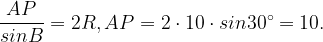
Тогда отрезок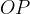 равен отрезку
равен отрезку 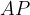 , т.е.
, т.е. 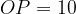 .
.
Найдем угол С из треугольника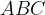 :
: 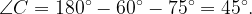
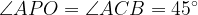 как вписанные углы, опирающиеся на дугу
как вписанные углы, опирающиеся на дугу  .
.
Площадь треугольника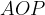 находится по формуле:
находится по формуле: 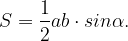
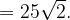
Ответ: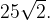
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания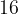 .
.
Значит,
Отсюда
Тогда
Ответ: 11.
Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.

Решение:
Пусть радиус вписанной окружности
Мы знаем, что в прямоугольном треугольнике
Значит,
Площадь находится по формуле
Ответ: 24.
Рассмотрим также задачу из 2 части ЕГЭ по математике.
Задача 12. Точка О – центр вписанной в треугольник
вторично пересекает описанную около треугольника
а) Докажите, что
б) Найдите площадь треугольника
Решение:
а) Пусть

Тогда
Значит,
б)

Угол
По теореме синусов для треугольника
Тогда отрезок
Найдем угол С из треугольника
Площадь треугольника
Ответ:
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания

